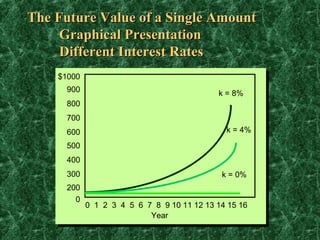
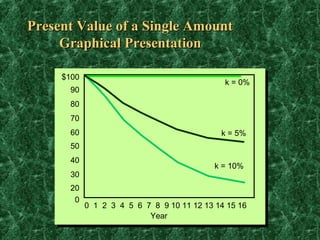
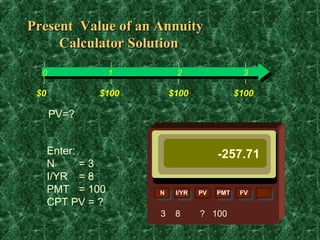
Let k = annual rate of return FV = PV(1+k)n 230 = 200(1+k)2 1.15 = (1+k)2 1.075 = 1+k .075 = k k = 7.5% annual return Therefore, the annual return on this investment is 7.5% Solving for k Example: You invest $1,000 today and want it to grow to $1,500 in 5 years. What rate of return is needed? 0 1 2 $1,000 $1,500

1. The Time Value
of Money

2. Learning Objectives
 The “time value of money” and its importance
to business.
 The future value and present value of a single
amount.
 The future value and present value of an
annuity.
 The present value of a series of uneven cash
flows.

3. The Time Value of Money
 Money grows over time when it earns
interest.
 Therefore, money that is to be received at
some time in the future is worth less than the
same dollar amount to be received today.
 Similarly, a debt of a given amount to be paid
in the future are less burdensome than that
debt to be paid now.
Link to FinanCenter

4. The Future Value of a Single Amount
 Suppose that you have $100 today and plan to put
it in a bank account that earns 8% per year.
 How much will you have after 1 year? 5 years?
15 years?
 After one year:
$100 + (.08 x $100) = $100 + $8 = $108
OR:
$100 (1.08)1 = $108

5. The Future Value of a Single Amount
 Suppose that you have $100 today and plan to put it
in a bank account that earns 8% per year.
 How much will you have after 1 year? 5? 15?
 After one year:
$100 (1.08)1 = $108
 After five years:
$100 (1.08)5 = $146.93
 After fifteen years:
$100 (1.08)15 = $317.22
 Equation:
FV = PV (1 + k)n

6. The Future Value of a Single Amount
Graphical Presentation
Different Interest Rates
$1000
900 k = 8%
800
700
600 k = 4%
500
400
300 k = 0%
200
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Year

7. Present Value of a Single Amount
 Value today of an amount to be received or
paid in the future.
PV = FVn x 1
n
(1 + k)
Example: Expect to receive $100 in one year. If can
invest at 10%, what is it worth today?
0 1 2
PV = 100 = 90.90 $100
(1.10)1

8. Present Value of a Single Amount
 Value today of an amount to be received or
paid in the future.
PV = FVn x 1
n
(1 + k)
Example: Expect to receive $100 in EIGHT years. If
can invest at 10%, what is it worth today?
0 1 2 3 4 5 6 7 8
100
PV =(1+.10)8 = 46.65 $100

9. Present Value of a Single Amount
Graphical Presentation
$100
k = 0%
90
80
70
60 k = 5%
50
40
k = 10%
30
20
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Year

10. Financial Calculator Solution - PV
Previous Example: Expect to receive $100 in EIGHT
years. If can invest at 10%, what is
it worth today?
100 = 46.65
Using Formula: PV =
(1+.10)8
Calculator Enter: - 46.65
N =8
I/YR = 10
FV = 100 N I/YR PV PMT FV
CPT PV = ? 8 10 ? 100

11. Financial Calculator Solution - FV
Previous Example: You invest $200 at 10%. How much
is it worth after 5 years?
Using Formula: FV = $200 (1.10)5 = $322.10

12. Financial Calculator Solution - FV
Previous Example: You invest $200 at 10%. How much
is it worth after 5 years?
Using Formula: FV = $200 (1.10)5 = $322.10
Calculator Enter:
N = 5 322.10
I/YR = 10
PV = -200
N I/YR PV PMT FV
CPT FV = ?
5 10 -200 ?

13. Annuities
 An annuity is a series of equal cash flows
spaced evenly over time.
 For example, you pay your landlord an
annuity since your rent is the same amount,
paid on the same day of the month for the
entire year.
Jan Feb Mar Dec
$500 $500 $500 $500 $500

14. Future Value of an Annuity
0 1 2 3
$0 $100 $100 $100
You deposit $100 each year (end of year) into a savings
account.
How much would this account have in it at the end of 3 years
if interest were earned at a rate of 8% annually?

15. Future Value of an Annuity
0 1 2 3
$0 $100 $100 $100
$100(1.08)2 $100(1.08)1 $100(1.08)0
$100.00
$108.00
$116.64
$324.64
You deposit $100 each year (end of year) into a savings
account.
How much would this account have in it at the end of 3
years if interest were earned at a rate of 8% annually?

16. Future Value of an Annuity
0 1 2 3
$0 $100 $100 $100
$100(1.08)2 $100(1.08)1 $100(1.08)0
$100.00
$108.00
$116.64
$324.64
How much would this account have in it at the end of 3 years
if interest were earned at a rate of 8% annually?
= 100 (1+.08) - 1 )
3
n
FVA = PMT( (1+k) - 1 )
( .08
k = 100(3.2464) = 324.64

17. Future Value of an Annuity
Calculator Solution
0 1 2 3
$0 $100 $100 $100
Enter:
N =3 324.64
I/YR = 8
PMT = -100
N I/YR PV PMT FV
CPT FV = ?
3 8 -100 ?

18. Present Value of an Annuity
 How much would the following cash flows be worth
to you today if you could earn 8% on your deposits?
0 1 2 3
$0 $100 $100 $100

19. Present Value of an Annuity
 How much would the following cash flows be worth
to you today if you could earn 8% on your deposits?
0 1 2 3
$0 $100 $100 $100
$100/(1.08)1 $100 / (1.08)2 $100 / (1.08)3
$92.60
$85.73
$79.38
$257.71

20. Present Value of an Annuity
 How much would the following cash flows be worth
to you today if you could earn 8% on your deposits?
0 1 2 3
$0 $100 $100 $100
$100/(1.08)1 $100 / (1.08)2 $100 / (1.08)3
$92.60
$85.73
$79.38
$257.71
1
1-
1
1 - (1+k)n = 100 ( (1.08)3
)
PVA = PMT( ) .08
k = 100(2.5771) = 257.71

21. Present Value of an Annuity
Calculator Solution
0 1 2 3
$0 $100 $100 $100
PV=?
Enter: -257.71
N =3
I/YR = 8
PMT = 100 N I/YR PV PMT FV
CPT PV = ?
3 8 ? 100

22. Annuities
 An annuity is a series of equal cash payments
spaced evenly over time.
 Ordinary Annuity: The cash payments occur
at the END of each time period.
 Annuity Due: The cash payments occur at the
BEGINNING of each time period.

23. Future Value of an Annuity Due
0 1 2 3
$100 $100 $100 FVA=?
You deposit $100 each year (beginning of year) into a
savings account.
How much would this account have in it at the end of 3 years
if interest were earned at a rate of 8% annually?

24. Future Value of an Annuity Due
0 1 2 3
$100 $100 $100
$100(1.08)3 $100(1.08)2 $100(1.08)1
$108
$116.64
$125.97
$350.61
You deposit $100 each year (beginning of year) into a
savings account.
How much would this account have in it at the end of 3 years
if interest were earned at a rate of 8% annually?

25. Future Value of an Annuity Due
0 1 2 3
$100 $100 $100
$100(1.08)3 $100(1.08)2 $100(1.08)1
$108
$116.64
$125.97
$350.61
How much would this account have in it at the end of 3
years if interest were earned at a rate of 8% annually?
n
= 100 (
(1+.08)3 - 1
.08
)
(1.08)
FVA = PMT( (1+k) - 1 ) (1+k)
k =100(3.2464)(1.08)=350.61

26. Present Value of an Annuity Due
 How much would the following cash flows be worth
to you today if you could earn 8% on your deposits?
0 1 2 3
$100 $100 $100
PV=?

27. Present Value of an Annuity Due
 How much would the following cash flows be worth
to you today if you could earn 8% on your deposits?
0 1 2 3
$100 $100 $100
$100/(1.08)0 $100/(1.08)1 $100 / (1.08)2
$100.00
$92.60
$85.73
$278.33

28. Present Value of an Annuity Due
 How much would the following cash flows be worth
to you today if you could earn 8% on your deposits?
0 1 2 3
$100 $100 $100
$100/(1.08)0 $100/(1.08)1 $100 / (1.08)2
$100.00
$92.60
$85.73
$278.33
1
1-
(1.08)3
1
1 - (1+k)n
= 100 ( .08
)
(1.08)
PVA = PMT( )(1+k)
k = 100(2.5771)(1.08) = 278.33

29. Amortized Loans
 A loan that is paid off in equal amounts that
include principal as well as interest.
 Solving for loan payments.

30. Amortized Loans
 You borrow $5,000 from your parents to purchase a
used car. You agree to make payments at the end of
each year for the next 5 years. If the interest rate on
this loan is 6%, how much is your annual payment?
0 1 2 3 4 5
$5,000 $? $? $? $? $?
ENTER:
N =5 –1,186.98
I/YR = 6
PV = 5,000
CPT PMT = ? N I/YR PV PMT FV
5 6 5,000 ?

31. Amortized Loans
 You borrow $20,000 from the bank to purchase a
used car. You agree to make payments at the end of
each month for the next 4 years. If the annual interest
rate on this loan is 9%, how much is your monthly
payment?
1
1-
(1.0075)48
$20,000 = PMT ( .0075
)
1
1 - (1+k)n
PVA = PMT( ) $20,000 = PMT(40.184782)
k
PMT = 497.70

32. Amortized Loans
 You borrow $20,000 from the bank to purchase a
used car. You agree to make payments at the end of
each month for the next 4 years. If the annual interest
rate on this loan is 9%, how much is your monthly
payment?
ENTER:
– 497.70
N = 48
I/YR = .75
PV = 20,000
N I/YR PV PMT FV
Note: CPT PMT = ?
N = 4 * 12 = 48 48 .75 20,000 ?
I/YR = 9/12 = .75

33. Perpetuities
 A perpetuity is a series of equal payments at equal
time intervals (an annuity) that will be received into
infinity.
PVP = PMT
k

34. Perpetuities
 A perpetuity is a series of equal payments at equal
time intervals (an annuity) that will be received into
infinity.
Example: A share of preferred stock pays a constant
dividend of $5 per year. What is the present
value if k =8%?
PVP = PMT
k

35. Perpetuities
 A perpetuity is a series of equal payments at equal
time intervals (an annuity) that will be received into
infinity.
Example: A share of preferred stock pays a constant
dividend of $5 per year. What is the present
value if k =8%?
PVP = PMT
k
If k = 8%: PVP = $5/.08 = $62.50

36. Solving for k
Example: A $200 investment has grown to $230 over
two years. What is the ANNUAL return on
this investment?
0 1 2
$200 $230
230 = 200(1+ k)2
1.15 = (1+ k)2
FV = PV(1+ k)n 1.15 = (1+ k)2
1.0724 = 1+ k
k = .0724 = 7.24%

37. Solving for k - Calculator Solution
Example: A $200 investment has grown to $230 over
two years. What is the ANNUAL return on
this investment?
Enter known values:
N =2 7.24
I/YR = ?
PV = -200
FV = 230 N I/YR PV PMT FV
Solve for: 2 ? -200 230
PMT. = ?

38. Compounding more than Once per Year
 $500 invested at 9% annual interest for 2 years.
Compute FV.
Compounding
Frequency
$500(1.09)2 = $594.05 Annual
$500(1.045)4 = $596.26 Semi-annual
$500(1.0225)8 = $597.42 Quarterly
$500(1.0075)24 = $598.21 Monthly
$500(1.000246575)730 = $598.60 Daily

39. Continuous Compounding
 Compounding frequency is infinitely large.
 Compounding period is infinitely small.
Example: $500 invested at 9% annual interest for
2 years with continuous compounding.
kn
FV = PV x e
FV = $500 x e.09 x 2 = $598.61