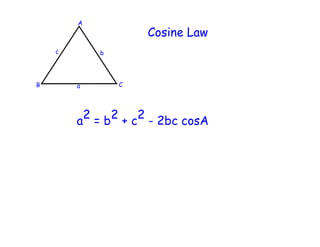
The document discusses the sine and cosine laws for solving triangles. It provides examples of using these laws to calculate missing angles and sides of triangles when given certain information. However, one of the examples leads to two possible triangle solutions, showing that the information provided an ambiguous case with multiple valid options. The summary concludes that without more context, both triangle solutions are considered correct since the given information allows for more than one possibility.

1. Sine and Cosine Laws!
The Review!

2. A
c b
B a C

3. A
c b
Sine Law
B a C
SinA SinB SinC
= =
a b c

4. A
A = 30° B=?
c b b=8 c=?
a=9 C=?
B a C
sin30 = sinB B = 26.4°
9 8
C = 180 - 30 - 26.4 = 125.4°
c = 9
c = 14.6
sin125.9 sin30

5. A
Cosine Law
c b
B a C
2 2 2
a = b + c - 2bc cosA

6. A
A = 30° B=?
c b
b=8 a=?
c=9 C=?
B a C
2 2 2
a = 8 + 9 - 2(8)(9) cos 30
a = 4.5
You can then use the sine law to find
the rest

7. Draw triangle ABC such that
∠A = 45°
a=6
b=7

8. Draw triangle ABC such that
∠A = 45° B
a=6 c a
b=7
A C
b
sin45 = sinB
B = 55.6
6 7
C = 180 - 45 - 55.6 = 79.4
c = 6 c = 8.34
sin79.4 sin45

9. But.....
...is there another possible triangle?

10. Draw triangle ABC such that
∠A = 45°
a=6
b=7
B a
c
A C
b

11. B
a
a
A C

12. B
a
B
a
A C

13. B1
B2 a
a
A C

14. B1 a
B1
a
A C

15. B1 a
B1
B2 a
A C
B2 = 180 - B1

16. B2
c a
A C
b
B2 = 180 - B1
B2 = 180 - 55.6 = 124.4
C2 = 180 - 124.4 - 45 = 10.6
c = 6
c = 1.56
sin10.6 sin45

17. This is called the Ambiguous Case. This
means that the information isn't perfectly
clear. The information leads to more than
1 possible solution.
Which is correct? Since there isn't any
more information given in the question to
help us determine which is the correct
triangle we say both are correct, since
both are possible.