This project utilized supervised algorithms to model individual income based on the 1994 U.S. census data, ultimately finding the Adaboost model most effective for predicting if individuals earn over $50,000. The Adaboost model achieved high performance metrics, including an F-score of 85% and accuracy of 86%, with significant features identified as capital-loss, age, and capital gain. The project's findings emphasize the model's appropriateness for binary classification while demonstrating low bias and variance, leading to robust generalization across test data.

1. Machine Learning
Case Study
1994 U.S. CENSUS

2. Objective of Project
Machine Learning Presentation | Introduction
In this project, several supervised algorithms were employed to accurately model individuals' income using data
collected from the 1994 U.S. Census. The best candidate algorithm was chosen from preliminary results and further
optimized to best model the data.
The goal in this project was to construct a model that accurately predicts whether an individual makes more than
$50,000. The first ten rows of the data set are shown below:

3. Top Findings
Machine Learning Presentation | Overview
• Adaboost is an appropriate model for this data - Based on the results, the AdaBoost model is most appropriate for the task of
identifying individuals that make more than $50,000
• Highest F-Score out of several models tested
• Low prediction/training time
• Highly suitable for binary classifications
• Model generalizes well to the test set at 10,000 observations and beyond
• High AUC (Area Under Curve) score: – .90
• Appropriate cut-off for test is around .97 for true positives and .58 for false positives (decision/classification threshold)
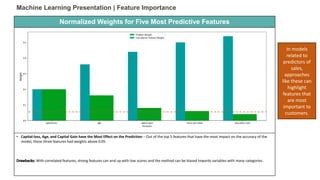
• Capital-loss, Age, and Capital Gain have the Most Effect on the Prediction – Out of the top 5 features that have the most impact
on the accuracy of the model, these three features had weights above 0.05
• Relatively High Model Scores:
• F-Score - 85% of cases where represented by a hormonic average of precision and recall [2 * (Precision * Recall)/(Precision
+ Recall)]
• Accuracy – 86% of predictions were correct [(True Positives + True Negatives) / All Values]

4. Performance Metrics for Three Supervised Learning Models
Machine Learning Presentation | Model Evaluation
• Based on the results, the AdaBoost model is most appropriate for the task of identifying individuals that make more than $50,000. This conclusion is based
on the following reasons:
• Out of the three models shown above, the AdaBoost model has the highest F-score on the testing set when 100% of the training data is used.
• The AdaBoost model has a low prediction/training time, especially when compared to the SVC model.
• AdaBoost is highly suitable for the data since the label is comprised of two binary classifications.
AdaBoost
model has the
highest F-score
on the testing
set

5. Confusion Matrix
Machine Learning Presentation | Scoring the Chosen Model
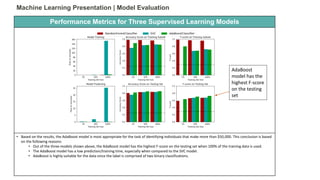
• Relatively High Model Scores:
• F-Score - 85% of cases where represented by a hormonic average of precision and recall [2 * (Precision * Recall)/(Precision +
Recall)]
• Accuracy – 86% of predictions were correct [(True Positives + True Negatives) / All Values]
• Precision – 85% of positive predictions were correct [True Positives/(True Positives + False Positives)]
• Recall – 86% of positive cases were true positives [True Positives/(True Positives + False Negatives)]
Categories Counts
True Positive 6431
True Negative 1342
False Positive 863
False
Negative
409
These numbers
are based on
predictions
generated by
an optimized
Adaboost
algorithm

6. ROC (Receiver Operating Characteristics) Curve
Machine Learning Presentation | ROC Curve for the Chosen Model
• Appropriate cut-off for test is around 97% for true positives and 58% for false positives (decision/classification threshold)
• Relatively high AUC (Area Under Curve) score:
• The AUC score is 90%
• The AUC scores using 5-fold cross-validation are 92%, 91%, 92%, 92%, and 91%
Appropriate cut-off
for test is around 97%
for true positives and
58% for false positives
These numbers
are based on
predictions
generated by
an optimized
Adaboost
algorthm

7. Learning Curve
Machine Learning Presentation | Bias and Variance
• The Learning Curve is satisfactory for the following reasons:
• There are reasonable prediction accuracies—probably because there are an adequate number of features leading to an acceptable model
complexity.
• Variance is low, so over-fitting is not prevalent and the model will generalize well on the test set.
• There is low bias.
• The regularization parameter is adequate.
• 10,000 Observations is adequate for Optimal Accuracy - At above the level of 10,000 observations, adding more observations will not lead to a more
accurate model because the two curves converge and remain converged.
Another
version of this
visualization
would use
Mean Squared
Error (MSE) as
a metric,
instead of
accuracy
Accuracy for
the test set
starts low
because it’s
unlikely that
the model can
generalize with
such low
instances of
observations.
Around 10,000
observations is
adequate for
optimal accuracy.

8. Normalized Weights for Five Most Predictive Features
Machine Learning Presentation | Feature Importance
• Capital-loss, Age, and Capital Gain have the Most Effect on the Prediction – Out of the top 5 features that have the most impact on the accuracy of the
model, these three features had weights above 0.05
With correlated features, strong features can end up with low scores and the method can be biased towards variables with many categories.
In models
related to
predictors of
sales,
approaches
like these can
highlight
features that
are most
important to
customers.