Download to read offline
Uploaded byGopi Krishna Nuti
Classification vis a-vis ranking - gopi
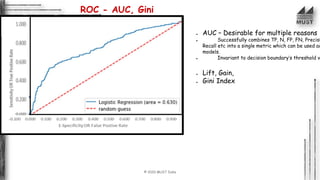
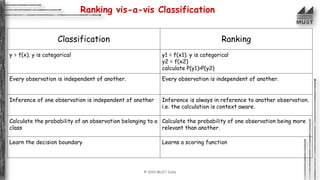
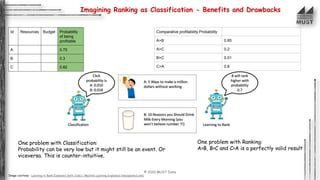
The document outlines the concepts of classification and ranking in machine learning, emphasizing predictive analytics and the distinction between supervised learning, regression, and classification tasks. It details various algorithms, metrics for evaluation such as confusion matrix and ROC-AUC, and discusses the complexities and decision boundaries of different classification models. Additionally, it introduces ranking approaches and algorithms, illustrating their applications in real-world scenarios like information retrieval and decision-making.
More Related Content
Similar to Classification vis a-vis ranking - gopi
Classification vis a-vis ranking - gopi
- 1. © 2020 MUSTIndia Classification Vis-a-vis Ranking in Machine Learning Gopi Krishna Nuti Vice President & Principal Researcher MUST Research ngopikrishna@gmail.com, vp@must.co.in
- 2. © 2020 MUSTIndia Classification
- 3. © 2020 MUSTIndia Classification
- 4. © 2020 MUSTIndia Classification • Predictive Analytics a.k.a. Supervised Learning • Observation’s features manifest a behaviour that can be expressed as y = f(x) • Y is discrete variable. Nominal or Ordinal • Examples: • Is this email a spam? • Fraud Detection Age Workclass Education Education-num MaritalStatus Occupation Relationship Race Gender hours-per-week AnnualIncome<=50K 39 State-gov Bachelors 13 Never-married Adm-clerical Not-in-family White Male 40 TRUE 50 Self-emp-not-inc Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 13 TRUE 38 Private HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 40 TRUE 53 Private 11th 7 Married-civ-spouse Handlers-cleaners Husband Black Male 40 TRUE 28 Private Bachelors 13 Married-civ-spouse Prof-specialty Wife Black Female 40 TRUE 37 Private Masters 14 Married-civ-spouse Exec-managerial Wife White Female 40 TRUE 49 Private 9th 5 Married-spouse-absent Other-service Not-in-family Black Female 16 TRUE 52 Self-emp-not-inc HS-grad 9 Married-civ-spouse Exec-managerial Husband White Male 45 FALSE 31 Private Masters 14 Never-married Prof-specialty Not-in-family White Female 50 FALSE 42 Private Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 40 FALSE y = f 𝑎𝑔𝑒, 𝑒𝑑𝑢𝑐𝑎𝑡𝑖𝑜𝑛 𝑛𝑢𝑚, ℎ𝑜𝑢𝑟𝑠 𝑝𝑒𝑟 𝑤𝑒𝑒𝑘
- 5. © 2020 MUSTIndia Odds 𝑜𝑑𝑑𝑠 = 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑒𝑣𝑒𝑛𝑡 ℎ𝑎𝑝𝑝𝑒𝑛𝑖𝑛𝑔 𝑝𝑟𝑜𝑏𝑎𝑏𝑖𝑙𝑖𝑡𝑦 𝑜𝑓 𝑒𝑣𝑒𝑛𝑡 𝑛𝑜𝑡 ℎ𝑎𝑝𝑝𝑒𝑛𝑖𝑛𝑔 If P is the probability of an event happening, then 𝑜𝑑𝑑𝑠 = 𝑃 1 − 𝑃 𝑙𝑛 𝑃 1 − 𝑃 = 𝛽0 + 𝛽1. 𝑥1 + 𝛽2. 𝑥2 + ⋯ . +𝛽 𝑛. 𝑥 𝑛 ො𝑦 = 𝛽0 + 𝛽1. 𝑥1 + 𝛽2. 𝑥2 + ⋯ . +𝛽 𝑛. 𝑥 𝑛 ∴ 𝑃 = 1 1 + 𝑒− ො𝑦
- 6. © 2020 MUSTIndia Binary Logistic Regression Age Workclass Education Education-num MaritalStatus Occupation Relationship Race Gender hours-per-week AnnualIncome<=50K 39 State-gov Bachelors 13 Never-married Adm-clerical Not-in-family White Male 40 TRUE 50 Self-emp-not-inc Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 13 TRUE 38 Private HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 40 TRUE 53 Private 11th 7 Married-civ-spouse Handlers-cleaners Husband Black Male 40 TRUE 28 Private Bachelors 13 Married-civ-spouse Prof-specialty Wife Black Female 40 TRUE 37 Private Masters 14 Married-civ-spouse Exec-managerial Wife White Female 40 TRUE 49 Private 9th 5 Married-spouse-absent Other-service Not-in-family Black Female 16 TRUE 52 Self-emp-not-inc HS-grad 9 Married-civ-spouse Exec-managerial Husband White Male 45 FALSE 31 Private Masters 14 Never-married Prof-specialty Not-in-family White Female 50 FALSE 42 Private Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 40 FALSE y = f 𝑎𝑔𝑒, 𝑒𝑑𝑢𝑐𝑎𝑡𝑖𝑜𝑛 𝑛𝑢𝑚, ℎ𝑜𝑢𝑟𝑠 𝑝𝑒𝑟 𝑤𝑒𝑒𝑘 If Annual Income <= 50K is considered as event, Probability of an observation being event = 1 1+𝑒−ෝ𝑦 This value is in range. (0,1).
- 7. © 2020 MUSTIndia Multi-class Classification • If dependent variable has multiple classes. For example : If Financial Status is the dependent variable, the possible classes are Low Income Class, Lower Middle Class, Upper Middle Class, Upper Class Multi-label Classification • y has multiple sets of labels and one label from each set can be applied to it. • For example: • Gmail sorts non spam email into multiple categories. Apart from Spam/Not Spam, emails are also categorized as Primary/ Updates/ Social/ Promotions/ Forums. An email will have two sets of labels to be applied. {Spam, Not Spam} and { Primary, Updates, Social, Promotions, Forums}. • Multi-label classification can be thought of as applying multi-class classification on the same data but for different sets of labels.
- 8. © 2020 MUSTIndia Metrics - Confusion Matrix ● Confusion Matrix ● TP, TN, FP, FN ● Precision, Recall, Specificity & Sensitivity What our model has predicted True False What the data really says True True Positives False Negatives False False Positives True Negatives 𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦 = 𝑇𝑃 + 𝑇𝑁 𝑇𝑃 + 𝑇𝑁 + 𝐹𝑁 + 𝐹𝑃 𝑃𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 = 𝑇𝑃 𝑇𝑁 + 𝐹𝑃 𝑅𝑒𝑐𝑎𝑙𝑙 = 𝑇𝑃 𝑇𝑃 + 𝐹𝑁 a.k.a Sensitivity 𝑆𝑝𝑒𝑐𝑖𝑓𝑖𝑐𝑖𝑡𝑦 = 𝑇𝑁 𝑇𝑁 + 𝐹𝑃 Which metric is the most important?
- 9. © 2020 MUSTIndia ROC - AUC, Gini ● AUC – Desirable for multiple reasons ● Successfully combines TP, N, FP, FN, Precisi Recall etc into a single metric which can be used ac models. ● Invariant to decision boundary’s threshold v ● Lift, Gain, ● Gini Index
- 10. © 2020 MUSTIndia Decision Boundary Linear decision boundary. Logistic regression can be a good choice. K-NN also works in this case. Non-linear decision boundary. SVM or decision trees. Logistic and k-NN may not be the best choice. Another Non-linear decision boundary.
- 11. © 2020 MUSTIndia Decision Boundary Complicated decision boundary. Neural Networks
- 12. © 2020 MUSTIndia Classification Algorithms Algorithm Applicable for Disadvantages Logistic Regression • Simple and linear decision boundary • Can be parallelized across machines with relative ease. Cannot handle non-linear decision boundaries Decision Tree & Random Forest • Reasonable tolerance to outliers. • Very intuitive and explainable. • Expensive to train. • Extremely susceptible to stochasticity • Can’t be parallelized across machines Support Vector Classification • Very useful for sparse data (common in NLP) • Very useful when there is no prior knowledge of data (Computer Vision) Cannot handle noise k-Nearest Neighbours • Depends on distance measure and similarity measures. • If, in the coordinate space, k datapoints belong to class A then the observation is also A. • Lazy learner. Does not learn decision boundary. Only memorizes the training dataset. Sort of like the student who only gets the subject “by rote”. Deep Learning • Complex decision boundaries can be learned. • Data hungry, computationally intensive. • Not explainable
- 13. © 2020 MUSTIndia References Please refer to “Machine Learning for Engineers” from MUST Research https://www.amazon.in/Machine-Learning-Engineers-Gopi- Krishna/dp/9389024870
- 14. © 2020 MUSTIndia Ranking
- 15. © 2020 MUSTIndia
- 16. © 2020 MUSTIndia Ranking - Introduction ● Supervised learning. Different from Regression and Classification. Learns “preference” or ordering of data. ● y = f(x) and y is categorical. ○ Much more than classification. ● Extensively used in Information Retrieval, Sentiment Analysis, Online Advertisements, Decision Making
- 17. © 2020 MUSTIndia Ranking - An intuitive scenario ● Company has 3 contracts. It can assign resources to only 1. Suggest the most profitable contract using ML? ● User has given a search string. 10 websites have qualified as having the relevant data. Which website is most appropriate? ● User is identified to be potential customer for diapers ad, alcohol ad and automobile ad. We can show only 1. Which is most relevant? Id Resources Budget Expected Profit Margin Time to Completion Bank Interest Rate Profitable (Y/N) A B C
- 18. © 2020 MUSTIndia Ranking vis-a-vis Classification Classification Ranking y = f(x). y is categorical y1 = f(x1). y is categorical y2 = f(x2) calculate P(y1)>P(y2) Every observation is independent of another. Every observation is independent of another. Inference of one observation is independent of another Inference is always in reference to another observation. i.e. the calculation is context aware. Calculate the probability of an observation belonging to a class Calculate the probability of one observation being more relevant than another. Learn the decision boundary Learns a scoring function
- 19. © 2020 MUSTIndia Imagining Ranking as Classification - Benefits and Drawbacks Id Resources Budget Probability of being profitable A 0.75 B 0.3 C 0.82 Comparative profitability Probability A>B 0.85 A>C 0.2 B>C 0.01 C>A 0.8 One problem with Ranking: A>B, B>C and C>A is a perfectly valid result Image courtesy : Learning to Rank Explained (with Code) | Machine Learning Explained (mlexplained.com) One problem with Classification: Probability can be very low but it might still be an event. Or viceversa. This is counter-intuitive.
- 20. © 2020 MUSTIndia Math behind Ranking ● Learns to directly sequence data by training a model to predict the probability of one observation ranking over another. ● Learns a scoring function where observations ranked higher shall have higher scores. The model can be trained via gradient descent on a loss function defined over these scores. ● Model a. inputs: a pair of observations A, B and their relative ranks b. outputs: Score for observation A > B c. Gradient descent function for optimizing the loss P rankA > rankB = 1 1 + 𝑒 𝛼 𝑠 𝐴−𝑠 𝐵
- 21. © 2020 MUSTIndia Ranking Approaches • Pointwise approach • Assumes that each observation and label in the training data has a numerical or ordinal score.— given a single observation-label pair, predict its score. Reduces ranking to regression/classification problem. • Pairwise approach Ranking is approximated by a classification function. i.e. a binary classifier which says A>B is True/False. The overall goal then changes to minimizing the average number of inversions in ranking. • Listwise approach • Directly optimize the evaluation measures (covered in next slide) and average them over all labels in the training data. • More difficult because evaluation measures are generally not continuous functions and require some approximations
- 22. © 2020 MUSTIndia Ranking Algorithms – A brief listing OPRF Polynomial regression (instead of machine learning, this work refers to pattern recognition, but the idea is the same) SLR Staged logistic regression Pranking Ordinal regression. McRank CRR Combined Regression and Ranking. Uses stochastic gradient descent to optimize a linear combination of a pointwise quadratic loss and a pairwise hinge loss from Ranking SVM. Pointwise DirectRanker Generalisation of the RankNet architecture RankNet Developed by Microsoft and rumoured to be the algorithm behind Bing search results LambdaRank RankNet in which pairwise loss function is multiplied by the change in the IR metric caused by a swap. LambdaSMART/ LambdaMART Based on Lambda-submodel-MART, or LambdaMART, Winning entry in the Yahoo Learning to Rank competition. Used an ensemble of LambdaMART models. Pairwise BayesRank A method combines Plackett-Luce Model and neural network to minimize the expected Bayes risk, related to NDCG, from the decision-making aspect. NDCG Boost A boosting approach to optimize NDCG. ES-Rank Evolutionary Strategy Learning to Rank technique FATE-Net/FETA-Net End-to-end trainable architectures, which explicitly take all items into account to model context effects. FastAP Optimizes Average Precision to learn deep embeddings Listwise
- 23. © 2020 MUSTIndia Ranking - Metrics Mean average precision (mAP) Average of scores calculated for a given set of queries. Conceptually similar to Precision in binary classification. NOT an average of precision values. Be mindful of this. Models with higher mAP are better. DCG and NDCG Normalized Discounted Cumulative Gain. This emphasizes on highly relevant observations being ranked higher. A higher DCG is preferable. Precision@n, NDCG@n "@n" denotes that the metrics are evaluated only on top n observations Mean reciprocal rank, Kendall's tau, Spearman's rho • In the context of Information Retrieval, getting a high Recall is trivial. Return all websites for all search results and 100% recall is achieved. • High Precision is highly desirable.
- 24. © 2020 MUSTIndia Ranking - Case studies • Extensive usage in information retrieval and online ads • Search Results • Document Retrieval • Highly applicable for decision making, fraud detection etc. • Choose the best course of action • Hypothetically, if only n patients can be saved from N (a painful scenario during the pandemic), how to decide the most eligible patients?
- 25. © 2020 MUSTIndia References • Foundation of ML Ranking - Mehryar Mohri, NYU • Ranking Methods in ML - Shivani Agarwal • Learning to Rank Using Classification and Gradient - Microsoft Research • Learning to Rank Explained (with Code) • LambdaMART Demystified - Tom´aˇs Tunys, Czech Technical University • Learning-to-rank with LightGBM (Code example in python)
- 26. © 2020 MUSTIndia Thanks Gopi Krishna Nuti Vice President & Principal Researcher MUST Research Created for Department of Information Technology Faculty Training Program (23-28 November 2020)