The document discusses Heaviside's unit step function, which is used to model abrupt changes in functions at specific times. It has a value of 0 for negative time and 1 for positive time. Shifted and delayed step functions are also discussed. The Laplace transform of various step functions is provided. Applications include modeling the switching on/off of voltages in electrical circuits and representing signals that switch at a given time.

1. Heaviside’s Unit Step Function

2. Introduction
The Unit Step Function(HeavisideFunction)
• In engineering applications, we frequently encounter functions
whose values change abruptly at specified values of time t. One
common example is when a voltage is switched on or off in an
electrical circuit at a specified value of time t.
• The value of t = 0 is usually taken as a convenient time to
switch on or off the given voltage.
• The switching process can be described mathematically by the
function called the Unit Step Function which is also known as
the Heaviside Unit Step function.

3. Heaviside’s Unit Step Function
• Definition: The unit step function is denoted as u(t) or H(t)
and is defined as
• That is, u is a function of time t, and u has value zero when
time is negative and value one when time is positive.
• Graphically it can be represented as :-

4. Laplace transform of Unit Step function H(t)
By definition of Laplace transform
𝐿 𝑓 𝑡 = 𝑓 𝑠 = 0
∞
𝑒−𝑠𝑡 𝑓 𝑡 𝑑𝑡
𝐿[𝑢 𝑡 ] = 𝑢̅ 𝑠 = 0
∞
𝑒−𝑠𝑡 𝑢 𝑡 𝑑𝑡
= 0
∞
𝑒−𝑠𝑡
1𝑑𝑡
= −
1
𝑠
0 − 1
=
1
𝑠
∴ 𝑳 𝒖 𝒕 = 𝒖 𝒔 =
𝟏
𝒔

5. Shifted Unit Step Function
• In many circuits, waveforms are applied at specified intervals
other than t = 0.
• Such a function may be described using the shifted /delayed
unit step function.
• A function which has value 0 up to the time t = a and
thereafter has value 1 is known as shifted unit step function
and is written as
• Graphically it can be represented as

6. Laplace Transform of Shifted
Unit Step Function H(t - a)
• 𝐿 𝐻 𝑡 − 𝑎 = 0
∞
𝑒−𝑠𝑡 𝐻 𝑡 − 𝑎 𝑑𝑡
= 0
𝑎
𝑒−𝑠𝑡 𝐻 𝑡 − 𝑎 𝑑𝑡 + 𝑎
∞
𝑒−𝑠𝑡 𝐻 𝑡 − 𝑎 𝑑𝑡
= 𝑎
∞
𝑒−𝑠𝑡
1 𝑑𝑡
= −
1
𝑠
(0 − 𝑒−𝑠𝑎)
∴ 𝑳[𝑯 𝒕 − 𝒂 ] =
𝒆−𝒂𝒔
𝒔

7. Unit Impulse Function
Rectangular Pulse
• A common situation in a circuit is for a voltage to be applied
at a particular time t = a and removed later, at t = b. We
write such a situation using unit step functions as
1 for a <t< b
• We can represent it graphically as :-
0 otherwise
u(t) =
t=a t=b0
1
u(t)

8. Laplace Transform of Impulse Function
• 𝐿[𝑢 𝑡 ] = 0
∞
𝑒−𝑠𝑡 𝑓 𝑡 𝑑𝑡
= 0
𝑎
𝑒−𝑠𝑡
𝑢 𝑡 𝑑𝑡 + 𝑎
𝑏
𝑒−𝑠𝑡
𝑢 𝑡 𝑑𝑡 + 𝑏
∞
𝑒−𝑠𝑡
𝑢 𝑡 𝑑𝑡
= 0
𝑎
𝑒−𝑠𝑡 (0) + 𝑎
𝑏
𝑒−𝑠𝑡 𝑢 𝑡 𝑑𝑡 + 𝑏
∞
𝑒−𝑠𝑡 (0)
= 𝑎
𝑏
𝑒−𝑠𝑡
∴ 𝑳[𝒖 𝒕 ] = −
𝟏
𝒔
[𝒆−𝒔𝒕 − 𝒆−𝒂𝒔]

9. Representation of a function using
Heaviside’s Functions
• It is more convenient to represent a function with the help of
unit step function
• A function f(t) can be represented in different ways using
Heaviside’s function.
i. F(t).H(t)
ii. F(t).H(t – a)
iii. F(t – a).H(t)
iv. F(t – a).H(t – b)
v. F(t) from t = a to t = b

10. Case 1 : F(t).H(t)
• We know that 𝐻 𝑡 =
0 𝑓𝑜𝑟 𝑡 < 0
1 𝑓𝑜𝑟 𝑡 ≥ 0
• Therefore multiplying f(t) with H(t), we get
f t . 𝐻 𝑡 =
0 𝑓𝑜𝑟 𝑡 < 0
𝑓(𝑡) 𝑓𝑜𝑟 𝑡 ≥ 0
• Hence by taking the product f(t).H(t) the part of f(t) to the left
of the origin is cut off.
• Example : Let 𝑓 𝑡 = 𝑡2
• f t . 𝐻 𝑡 =
0 𝑓𝑜𝑟 𝑡 < 0
𝑡2
𝑓𝑜𝑟 𝑡 ≥ 0

11. Case 2 : F(t).H(t - a)
• We know that 𝐻 𝑡 − 𝑎 =
0 𝑓𝑜𝑟 𝑡 < 𝑎
1 𝑓𝑜𝑟 𝑡 ≥ 𝑎
• Therefore multiplying f(t) with H(t - a), we get
𝑓 𝑡 . 𝐻 𝑡 − 𝑎 =
0 𝑓𝑜𝑟 𝑡 < 𝑎
𝑓(𝑡) 𝑓𝑜𝑟 𝑡 ≥ 𝑎
• Hence by taking the product f(t).H(t-a) the part of f(t) to
the left of the t = a is cut off.
• Example: Let 𝑓 𝑡 = 𝑡2
• 𝑓 𝑡 . 𝐻 𝑡 =
0 𝑓𝑜𝑟 𝑡 < 𝑎
𝑡2 𝑓𝑜𝑟 𝑡 ≥ 𝑎
Here a = 2

12. Case 3 : F(t - a).H(t)
• We know the curve 𝑦 = 𝑓 𝑥 − 𝑎 is same as 𝑦 = 𝑓 𝑥 only
difference is that the origin is shifted at a.
• Hence the shape of the curve remains unchanged.
• Therefore 𝑓 𝑡 − 𝑎 . 𝐻 𝑡 =
0 𝑓𝑜𝑟 𝑡 < 𝑎
𝑓(𝑡) 𝑓𝑜𝑟 𝑡 ≥ 𝑎
𝒇 𝒕 − 𝒂 . 𝑯 𝒕 will represent the curve 𝒇 𝒕 − 𝒂 on the
right of origin.

13. Case 4 : F(t - a).H(t - b)
f(t - a).H(t - b) will give the part of the shifted curve f(t - a) to
the right of t = b cutting off the part before t = b
• Since f(t-a) is the curve f(t) with origin shifted to a.
• Here H(t-b) is zero before t = b and unity after t = b.
• Therefore 𝑓 𝑡 − 𝑎 . 𝐻 𝑡 − 𝑏 =
0 𝑓𝑜𝑟 𝑡 < 𝑏
𝑓(𝑡 − 𝑎) 𝑓𝑜𝑟 𝑡 ≥ 𝑏

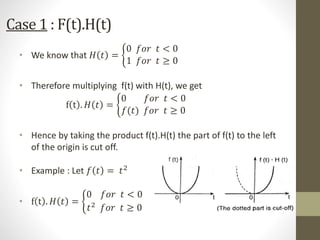
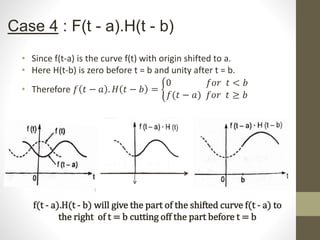
14. Case 5 : Representation of the part of the
curve f(t) from t = a to t = b
• We see that H(t-a) is a unit function on the right of t=a and H(t-b)
on the right of t=b.
• So the function [H(t-a)- H(t-b)] is zero before t=a and after t=b.
• Therefore here H(t)= 𝐻 𝑡 =
1 𝑓𝑜𝑟 𝑎 < 𝑡 < 𝑏
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
Hence the only remaining part of f(t). [H(t-a)- H(t-b)] is between
t=a and t=b called as filter function.

15. Applications of Heaviside’s Unit
Step Function

16. Where do we use it?
 The function is commonly used in the mathematics of
control theory and signal processing.
Heaviside’s unit step function represents unit output of a
system with possible time lead or lag
 It is used to calculate currents when electric circuit is
switches on.
 It represents a signal that switches on at a specified
time stays switched on indefinitely.

17. How do we use it?
 Heaviside functions can only take values 0 or 1, but we can also
use them to get other kinds of switches.
 Example: 4uc(t) is a switch that is off until t = c and then turns on
and takes a value 4.
 Now, suppose we want a switch that is on (with a value 1) and
then turns off at t = c.
 We can represent this by 1 – uc(t) = {1 – 0 = 1} ; if 𝑡 < 𝑐
= {1 – 1 = 0} ; if 𝑡 ≥ 𝑐