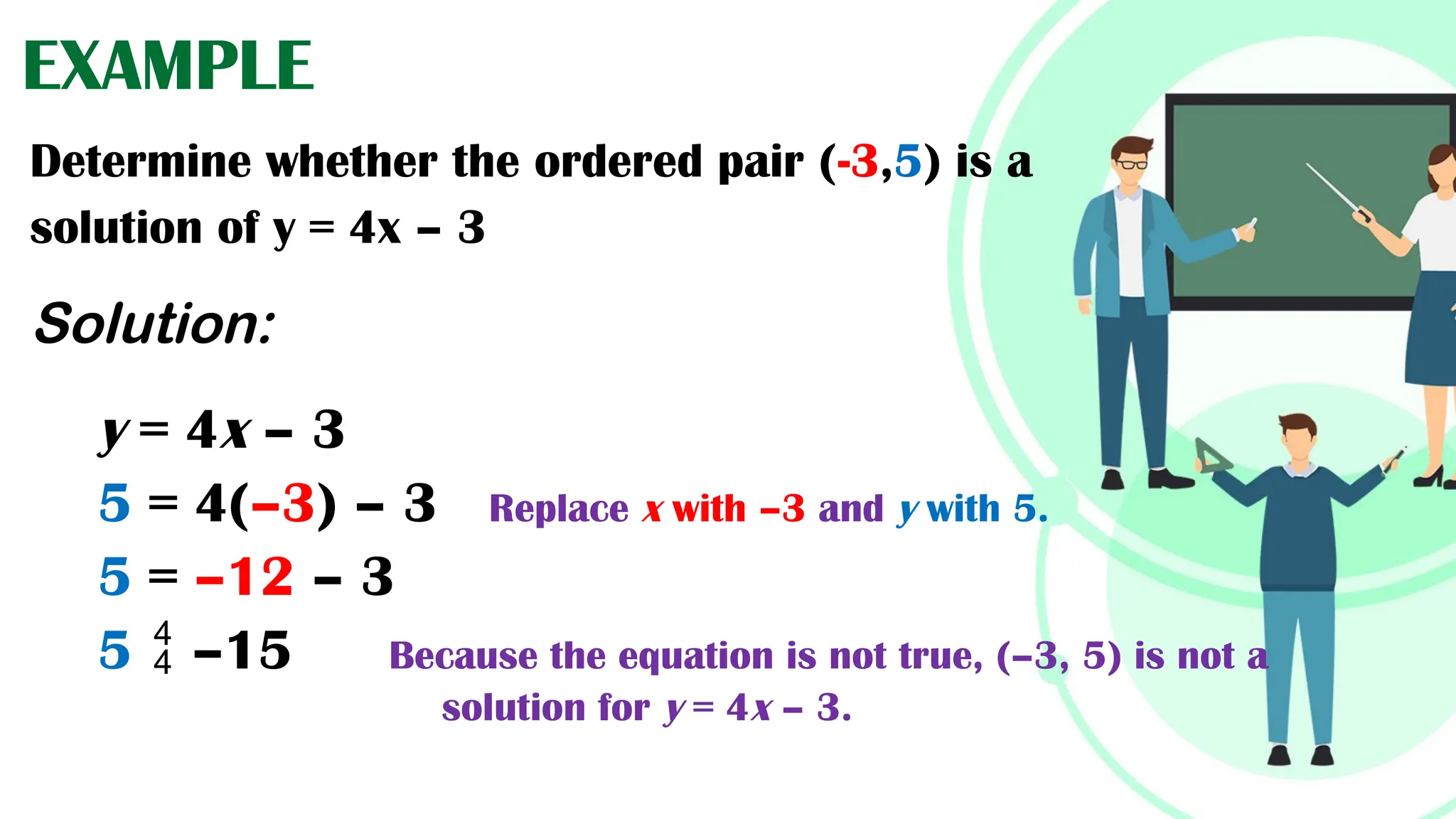
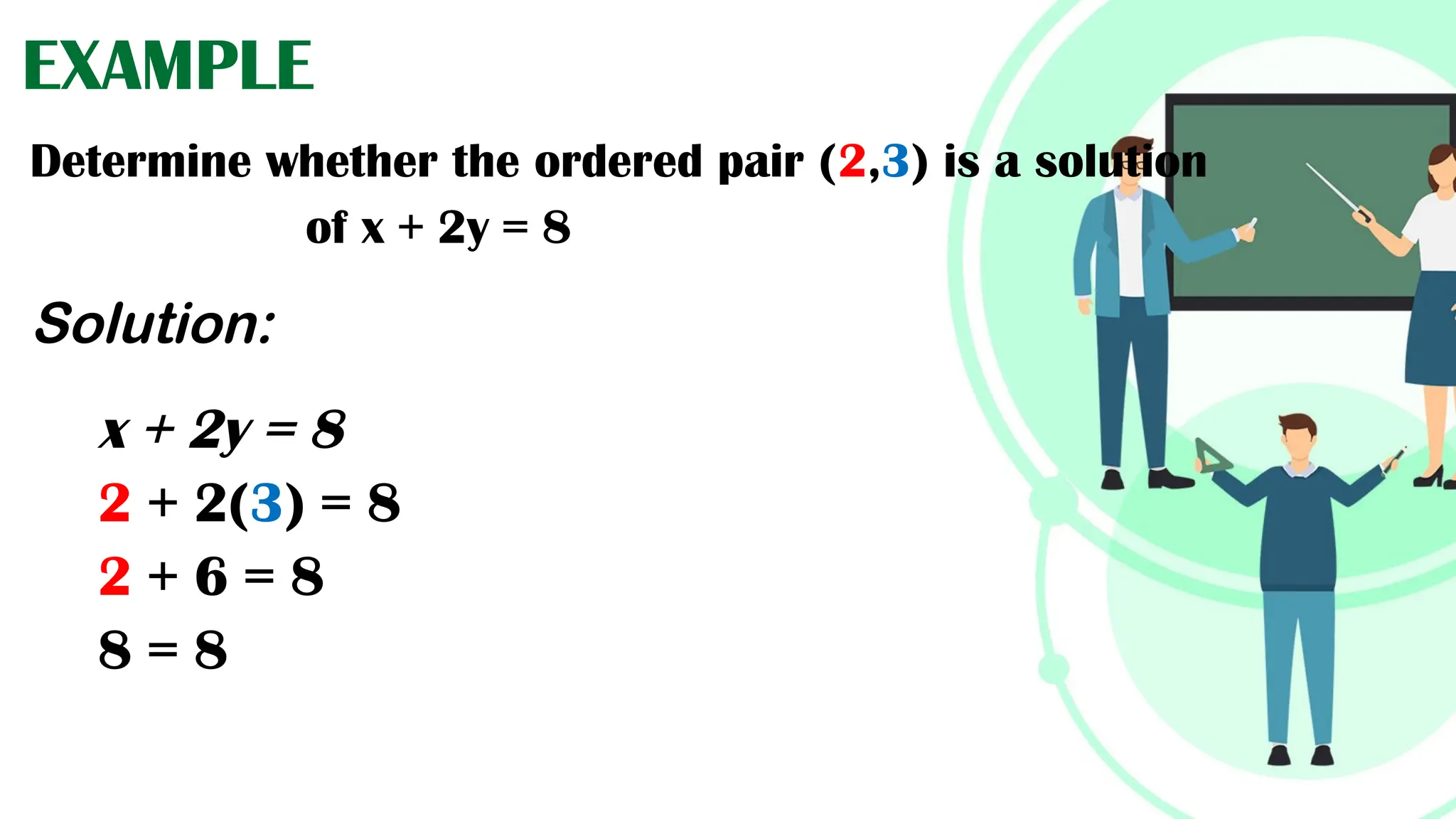
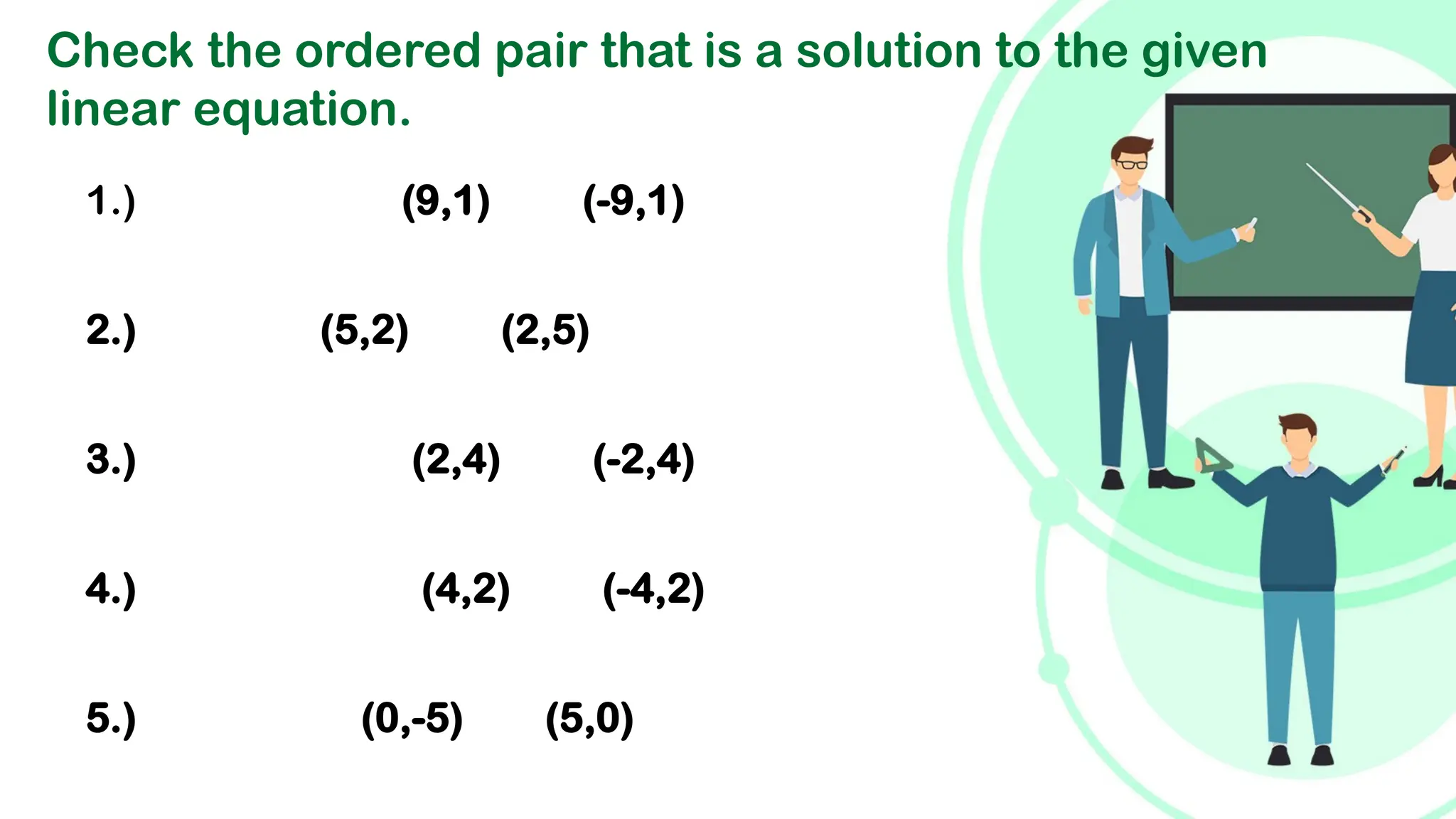
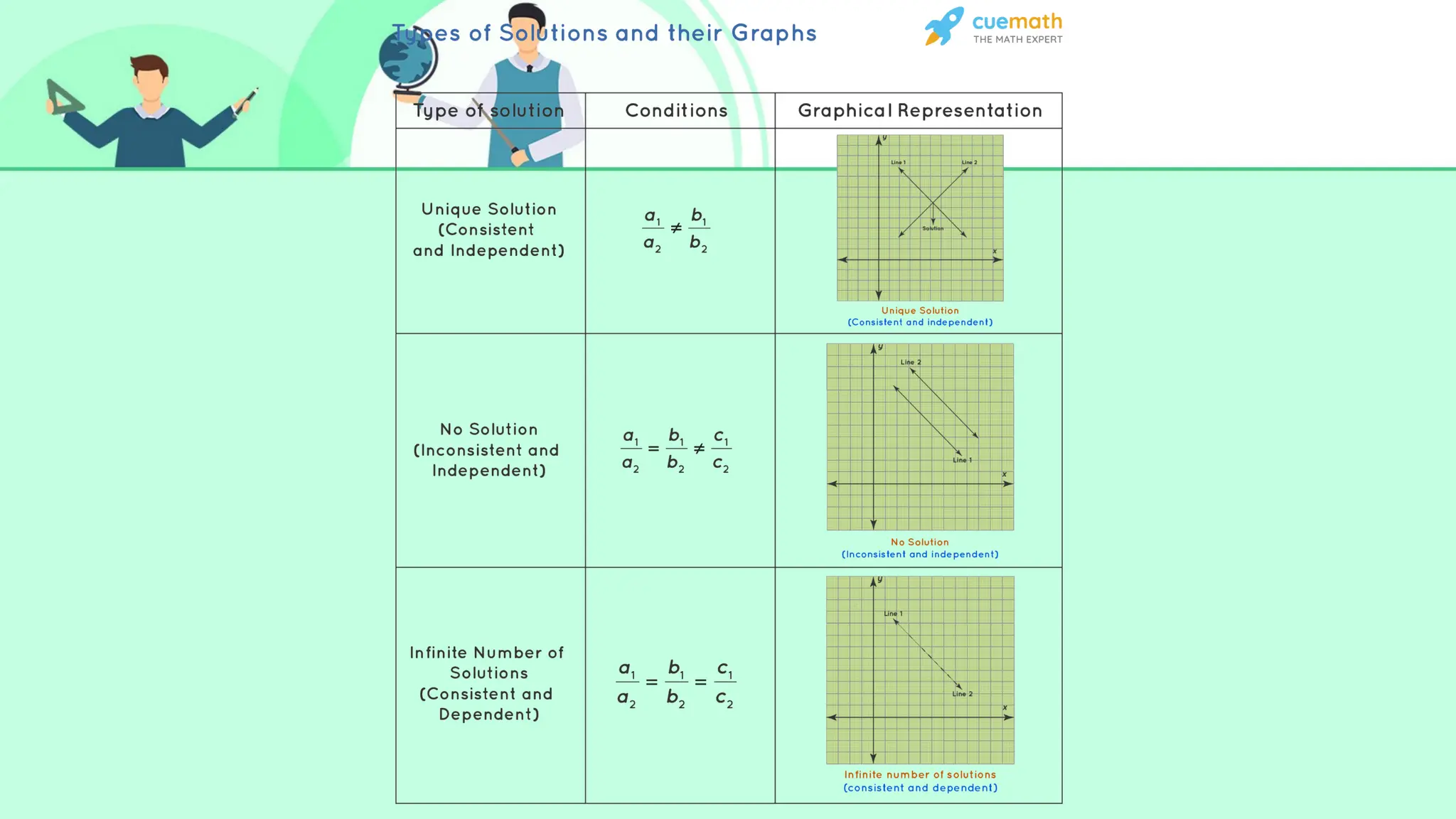
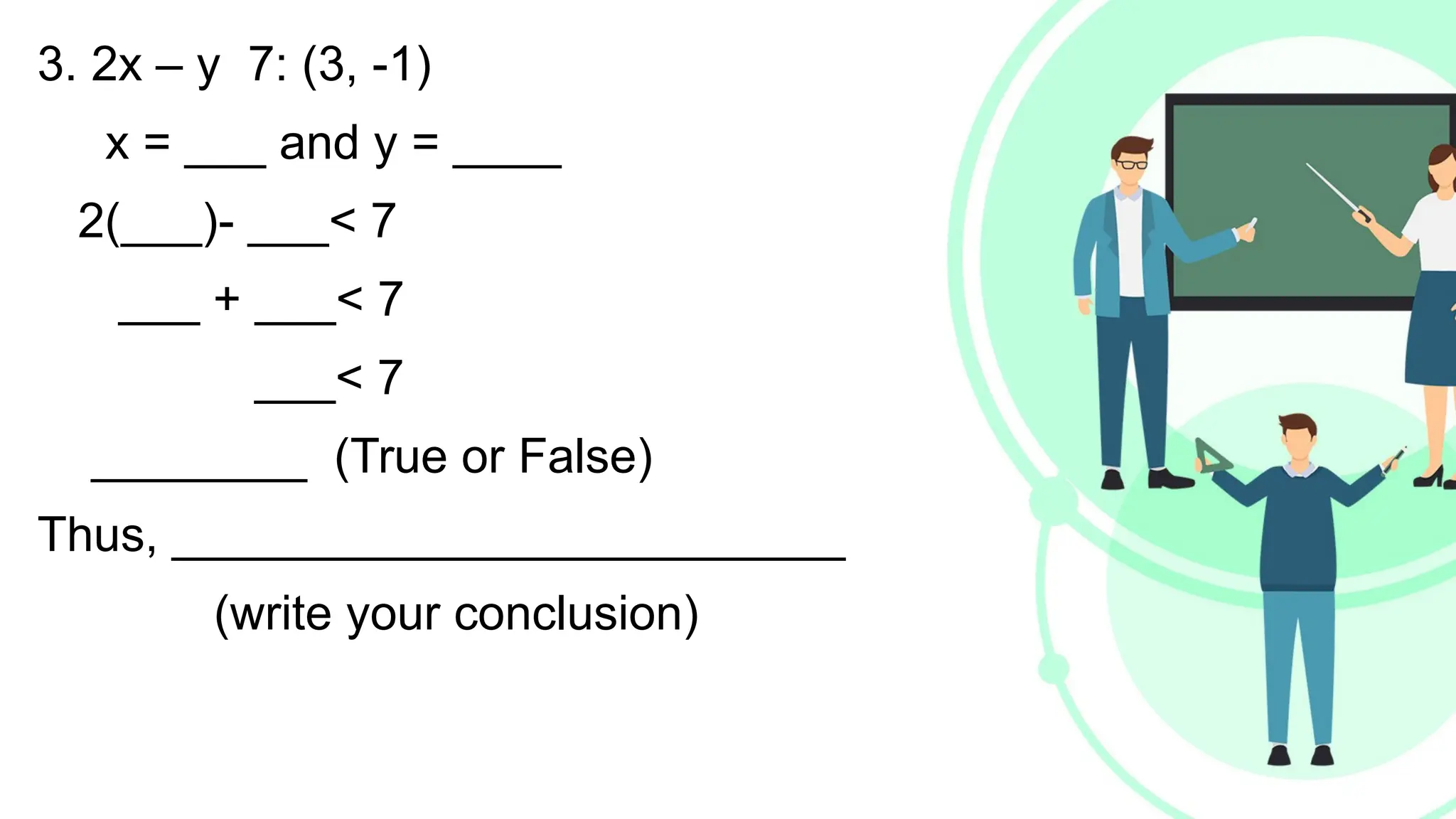
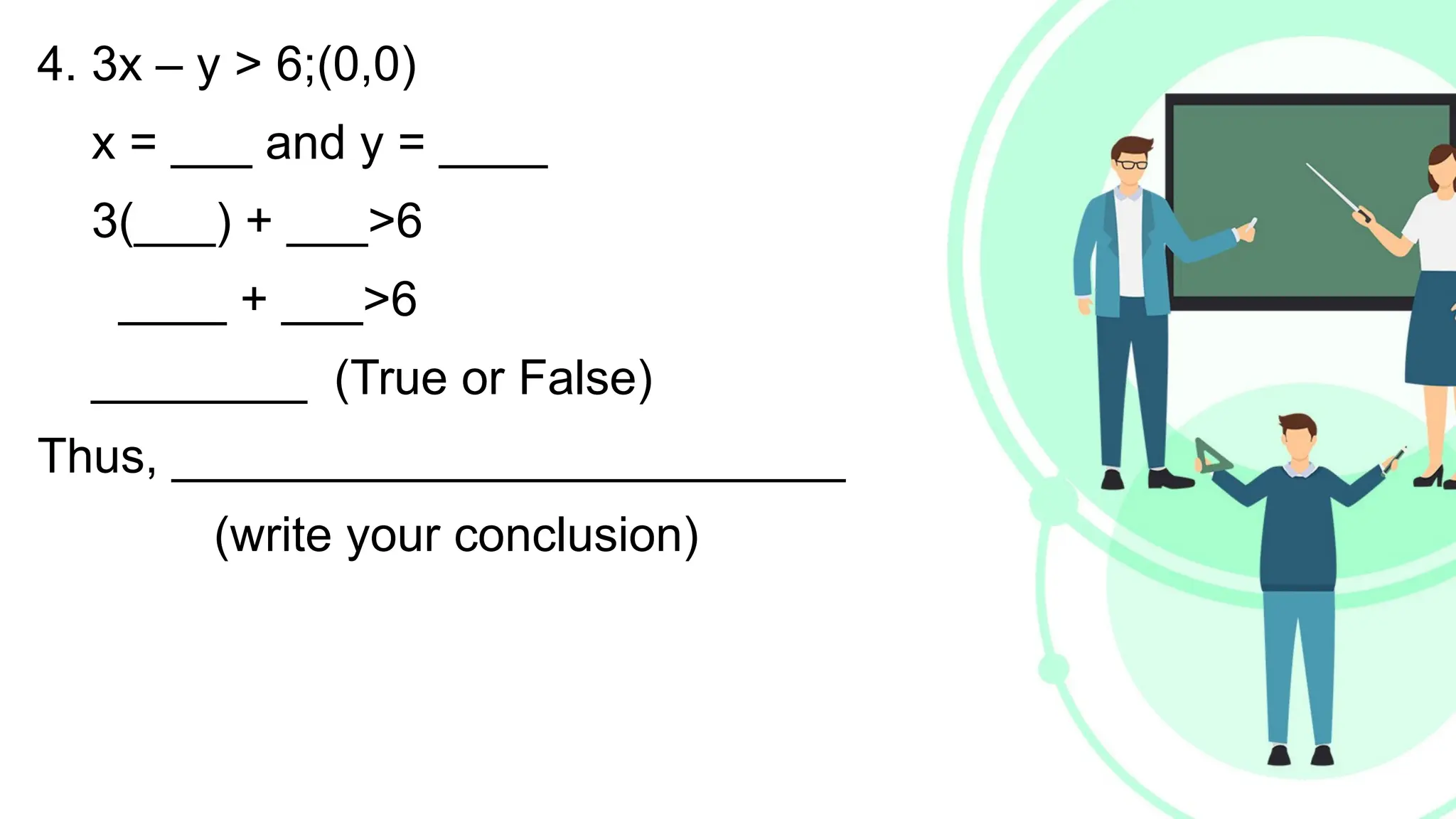
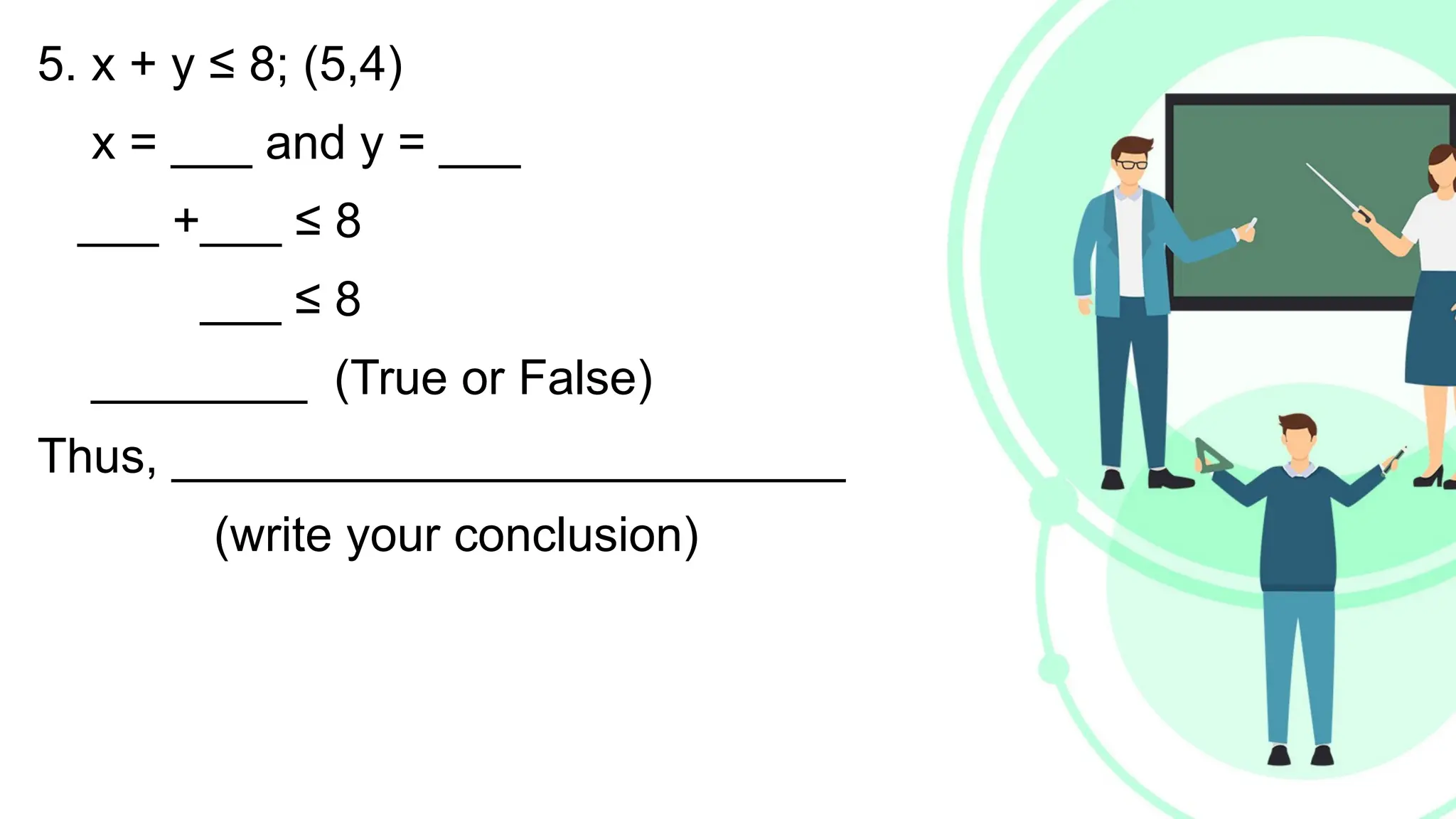
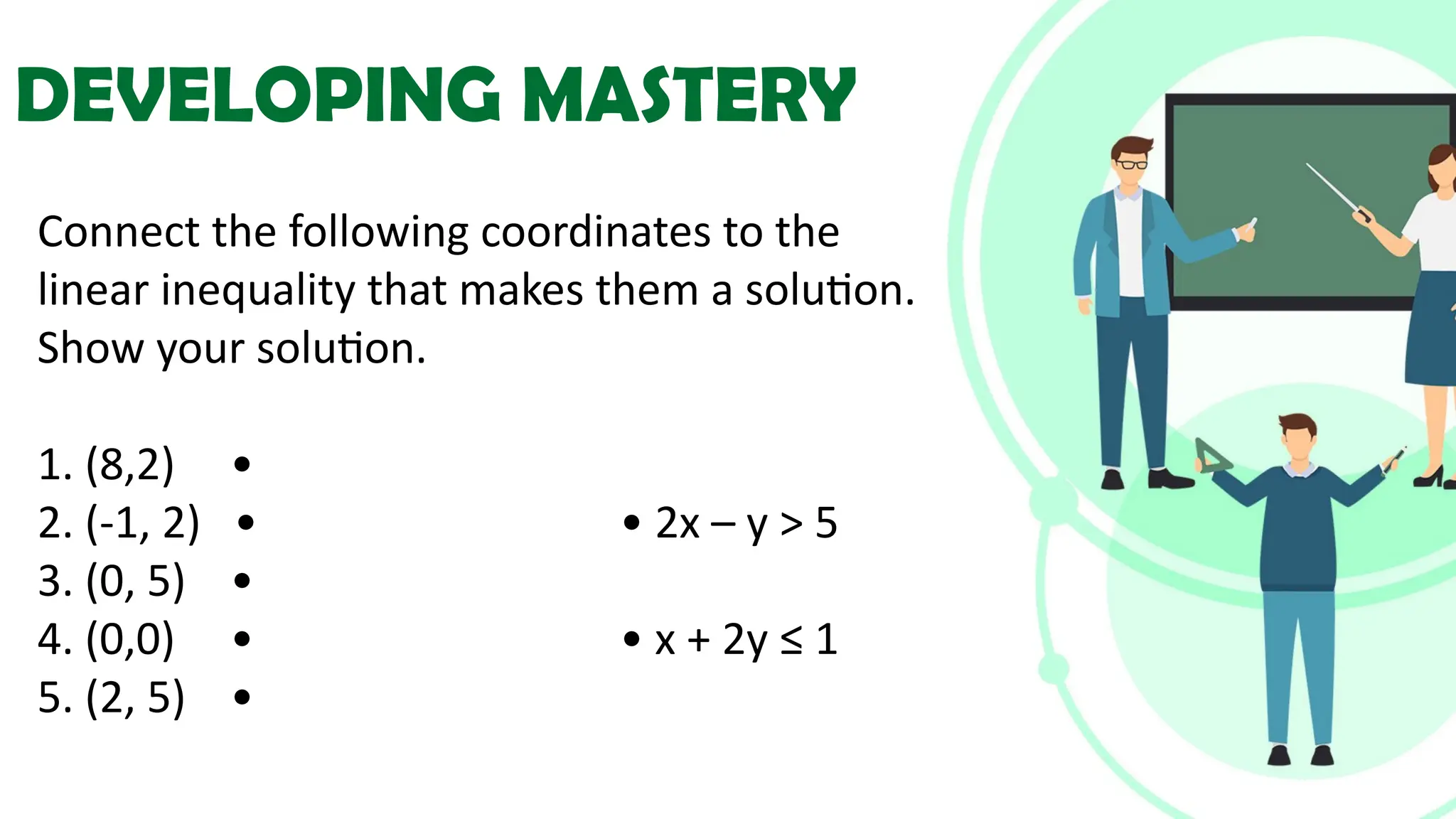
Linear equations in two variables are expressed as ax + by + c = 0, where a, b, and c are real numbers and a and b are non-zero, commonly used in geometry for line coordinates. Solutions are ordered pairs (x, y) that satisfy the equation, with techniques to verify and determine solutions for given points or inequalities. The document also covers converting equations between standard and slope-intercept forms, alongside examples and applications involving linear inequalities.

1. ILLUSTRAT
E LINEAR
EQUATION
IN TWO
VARIABLES

2. What are Linear Equations in Two Variables?
• Linear equations in two variables is an equation of the
form ax + by + c = 0, where x and y are the two
variables and a, b, and c are real numbers and a and b
are non-zero.
• It is popularly known as simultaneous linear equation.
Linear equations in two variables are usually used in
geometry to find the coordinates of a straight line.
• Example: x+y–3=0 is a linear equation in two
variables x and y

3. Solutions of Linear Equations in Two
Variables
• The solution of a linear equation
ax+by=c, where a, b and c are constants
are the set of ordered pair (x,y) that will
satisfy the equation or that will make the
equation true. To find the solution of a
linear equation in two variables, we
usually express one variable in terms of
the other variable

4. EXAMPLE
Determine whether the ordered pair (-3,5) is a
solution of y = 4x – 3
Solution:
y = 4x – 3
5 = 4(–3) – 3 Replace x with –3 and y with 5.
5 = –12 – 3
5  –15 Because the equation is not true, (–3, 5) is not a
solution for y = 4x – 3.

5. EXAMPLE
Determine whether the ordered pair (2,3) is a solution
of x + 2y = 8
Solution:
x + 2y = 8
2 + 2(3) = 8
2 + 6 = 8
8 = 8

6. Check the ordered pair that is a solution to the given
linear equation.
1.) (9,1) (-9,1)
2.) (5,2) (2,5)
3.) (2,4) (-2,4)
4.) (4,2) (-4,2)
5.) (0,-5) (5,0)

7. Check the ordered pair that is a solution to the given
linear equation.
1.) (9,1) (-9,1)
2.) (5,2) (2,5)
3.) (2,4) (-2,4)
4.) (4,2) (-4,2)
5.) (0,-5) (5,0)

8. “TRY ME”
Determine if the given ordered pair is the solution of linear
equation in two variables. (SOLUTION or NOT)
1.) 5x – y = -1 (1,6)
2.) 4x + 5y = 10 (2,4)
3.) y = 3x + 2 (2,8)
4.) y = 4x + 1 (4,17)

9. INDIVIDUAL ACTIVITY
Determine the solution of linear equation in two variables.
1.) y = 4x + 1
2.) y = -2x + 6
3.) 3x + y = 9
x -2 -1
y
x 2 4
y
x 1 3
y

11. Linear
Inequalities in
Two Variables vs
Linear Equations
in Two Variables.

12. Objectives
a. Identify the solution of a linear equation or
inequality in two variables.
b. Determine whether a point is a solution of a
linear inequality or not.
c. Appreciate the concept of linear inequality in
two variables.

13. REVIEW
Which of the following points is a solution to the
following linear inequalities? Explain your answer.
1. 2x – y > - 3 (3, 6) (4, 11) (2, 7)
2. y ≥ -6x + 1 (2, -11) (-3, -8) (-5, 6)
3. 5x + y > 10 (0, -3) (3, -5) (4, 8)
4. y ≤ x - 9 (2, -5) (9, -3) (12, 3)
5. y < 5x -3 (3, 5) (2, 7) (3, 0 )

14. EXAMPLES
The points (2, 7), (0, 3) and (-1, 1) are the points on
the line y = 2x + 3 and the solutions to the given
equation.
Determine if the points (5, 8), (0, 0), and (10, 10) are
solutions to the linear inequality 2x + 5y > 10.
Linear EQUALITY in two variable
Linear INEQUALITY in two variable

15. 1. What can you say about the
solution of a linear equation?
2. When can you say that a point is
a solution to a linear inequality in
two variables?
3. How can you solve if a point is a
solution to a linear equation or
inequality in two variables?

16. Fill in the blanks then state whether each given
ordered pair is a solution of the inequality.
1. x + 2y ≤ 8; (6,1)
x = ___ and y = ___
___ + 2 (___) ≤ 8
6 + ___ ≤ 8
___ ≤ 8
________ (True or False)
Thus, _________________________
(write your conclusion)

17. 2. x - ≥ -2: (-6, -8)
x = ___ and y = ___
___ - ( ___)≥-2
-6 + ___≥-2
___≥-2
________ (True or False)
Thus, _________________________
(write your conclusion)

18. 3. 2x – y 7: (3, -1)
x = ___ and y = ____
2(___)- ___< 7
___ + ___< 7
___< 7
________ (True or False)
Thus, _________________________
(write your conclusion)

19. 4. 3x – y > 6;(0,0)
x = ___ and y = ____
3(___) + ___>6
____ + ___>6
________ (True or False)
Thus, _________________________
(write your conclusion)

20. 5. x + y ≤ 8; (5,4)
x = ___ and y = ___
___ +___ ≤ 8
___ ≤ 8
________ (True or False)
Thus, _________________________
(write your conclusion)

21. Connect the following coordinates to the
linear inequality that makes them a solution.
Show your solution.
1. (8,2) •
2. (-1, 2) • • 2x – y > 5
3. (0, 5) •
4. (0,0) • • x + 2y ≤ 1
5. (2, 5) •
DEVELOPING MASTERY

22. Determine 2 solution for each of the
following linear inequalities. Show your
solution.
1. 5x + 2y < 17 ; x = 3
2. 3x - 8y ≤ 12 ; x = 0
3. - 10x - 2y > 7 ; x = -2
4. x + 5y ≥ 20 ; y = -1
5. 3x +2y < 21 ; y = 4
APPLICATION

23. • The solution of a linear equation
is the set of points which lies on the
line.
• A solution of a linear inequality in
two variables is an ordered pair (x, y)
which makes the equation or inequality
true.
GENERALIZATION

24. EVALUATION
Which of the following points is a solution to the
following equations/ inequalities? Encircle your
answer/s.
1. 3x + y > - 6 (3, 6) (4, 11) (2, 7)
2. y > 5x + 2 (2, -11) (-3, -8) (-5, 6)
3. -3x + 6y ≥ 10 (0, -3) (3, -5) (4, 8)
4. y ≤ 2x - 5 (2, -5) (9, -3) (12, 3)
5. 2y < 5x + 3 (3, 5) (2, 7) (3, 0)

25. ADDITIONAL ACTIVITY
1. a. Which ordered pair satisfies the inequality
3/2 x - 1/4y ≤ 1 ?
a. (0, -5) b. (3, -5) c. (0, 1) d. (6, 0)
b. Graph x + y = 6 in a Cartesian plane. Identify 5
points which are solution of the inequality x + y > 6,
then plot them on the same plane. Make a conjecture
about it.
2. Study how to graph linear inequality in two variables.
Write the step by step process on your notebook.

26. Rewriting Linear Equations
in Two Variables
Ax+ By = C in the form
y= mx + b and vice versa

27. Slide Title
Product A
• Feature 1
• Feature 2
• Feature 3
Product B
• Feature 1
• Feature 2
• Feature 3

28. The process of rewriting linear equations in
two variables Ax + By = C in the form y = mx +
b can be done by solving y in terms of x.
While, the process of rewriting linear
equations in two variables, y = mx + b in the
form Ax + By = C can be done by applying the
different properties of real numbers and
equations of Ax and By on the left- side of the
equation and equate it to the constant term C
on the right side.

29. Illustrative Examples:
1. 3x - 2y=4
- 2y = -3x+4 Solve y in terms of x
- ( - 2y = -3x+4)-1/2 Apply MPE
y = 3x/2 – 2 Simplify
2. y= 5x + 6
-5x + y =6 Sum of Ax and By on the left- hand side of
the equation and equate it to the constant
term C on the right- hand side
- ( -5x + y = 6 ) Apply MPE
5x + y = 6 Simplify

30. ACTIVITY
STANDARD FORM SLOPE-INTERCEPT FORM
1.) x – 3y =6
2.) 2x + 2y = -10
3.) y = -2x + 6
4.) y = 3x + 5

31. ACTIVITY
STANDARD FORM SLOPE-INTERCEPT FORM
1.) x – 3y =6 (– 3y =-x + 6) ÷ -3
y = 3x + 2
2.) 2x + 2y = -10 (2y = -2x – 10) ÷ 2
y = -x – 5
y = -2x + 6
2x + y = 6
3.) y = -2x + 6
y = 3x + 5
(-3x + y = 5) times -1
3x – y = -5
4.) y = 3x + 5

32. Illustrative Examples:
1. 3x - 2y=4
- 2y = -3x+4 Solve y in terms of x
- ( - 2y = -3x+4)-1/2 Apply MPE
y = x – 2 Simplify
2. y= 5x + 6
-5x + y =6 Sum of Ax and By on the left- hand side of
the equation and equate it to the constant
term C on the right- hand side
- ( -5x + y = 6 ) Apply MPE
5x + y = 6 Simplify

33. Two-Point Form
𝑦 − 𝑦 1
𝑥 − 𝑥1
=
𝑦2− 𝑦1
𝑥2− 𝑥1
Where () and () are two
points on the line

34. Illustrative Examples:
1. 3x - 2y=4
- 2y = -3x+4 Solve y in terms of x
- ( - 2y = -3x+4)-1/2 Apply MPE
y = x – 2 Simplify
2. y= 5x + 6
-5x + y =6 Sum of Ax and By on the left- hand side of
the equation and equate it to the constant
term C on the right- hand side
- ( -5x + y = 6 ) Apply MPE
5x + y = 6 Simplify

35. Illustrative Examples:
1. 3x - 2y=4
- 2y = -3x+4 Solve y in terms of x
- ( - 2y = -3x+4)-1/2 Apply MPE
y = x – 2 Simplify
2. y= 5x + 6
-5x + y =6 Sum of Ax and By on the left- hand side of
the equation and equate it to the constant
term C on the right- hand side
- ( -5x + y = 6 ) Apply MPE
5x + y = 6 Simplify
Point (4, 5) Point (-7, -17)
𝑦 − 𝑦 1
𝑥 − 𝑥1
=
𝑦2 − 𝑦1
𝑥2 − 𝑥1
𝑦 −5
𝑥 − 4
=
−17 −5
−7 − 4