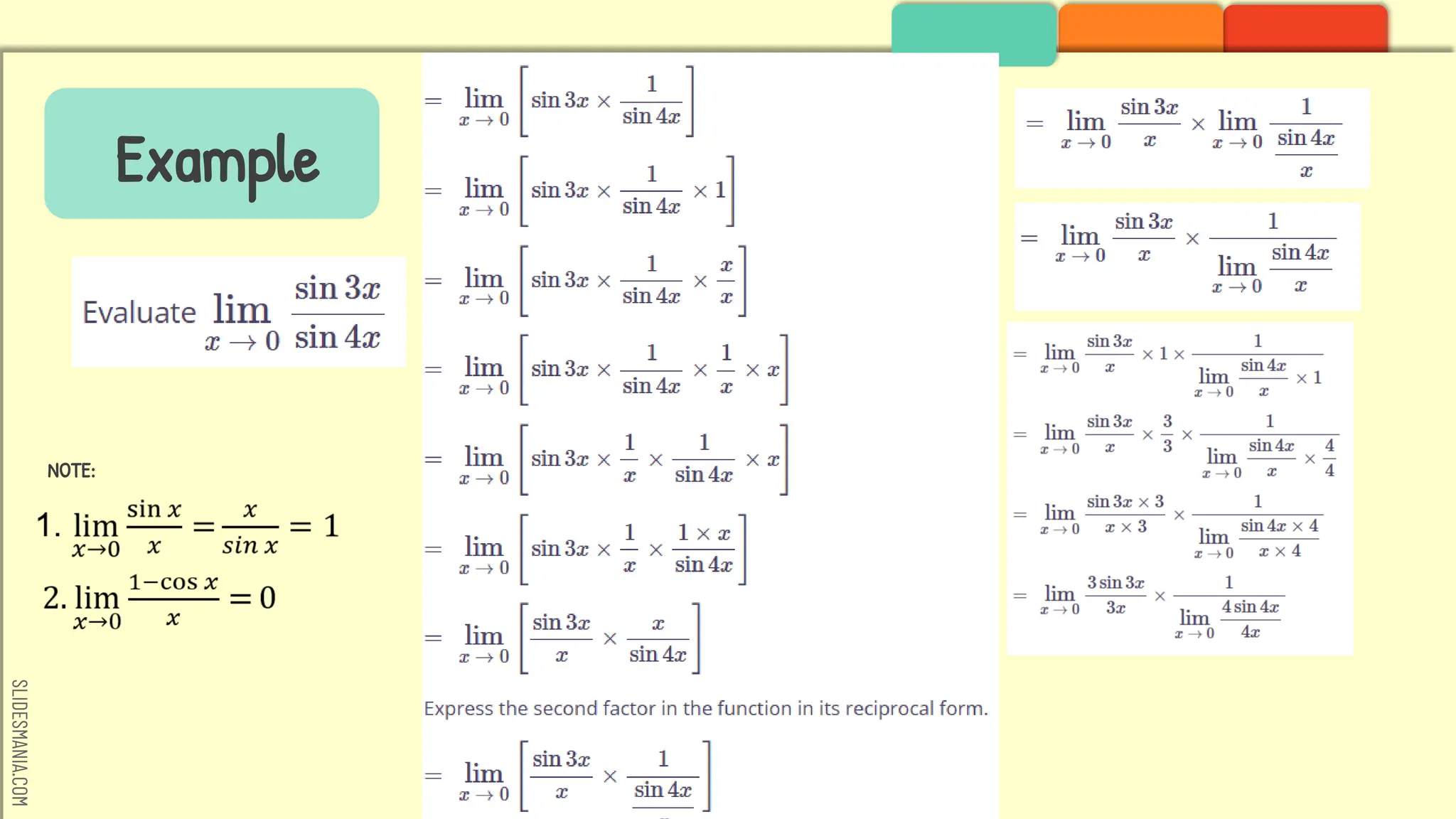
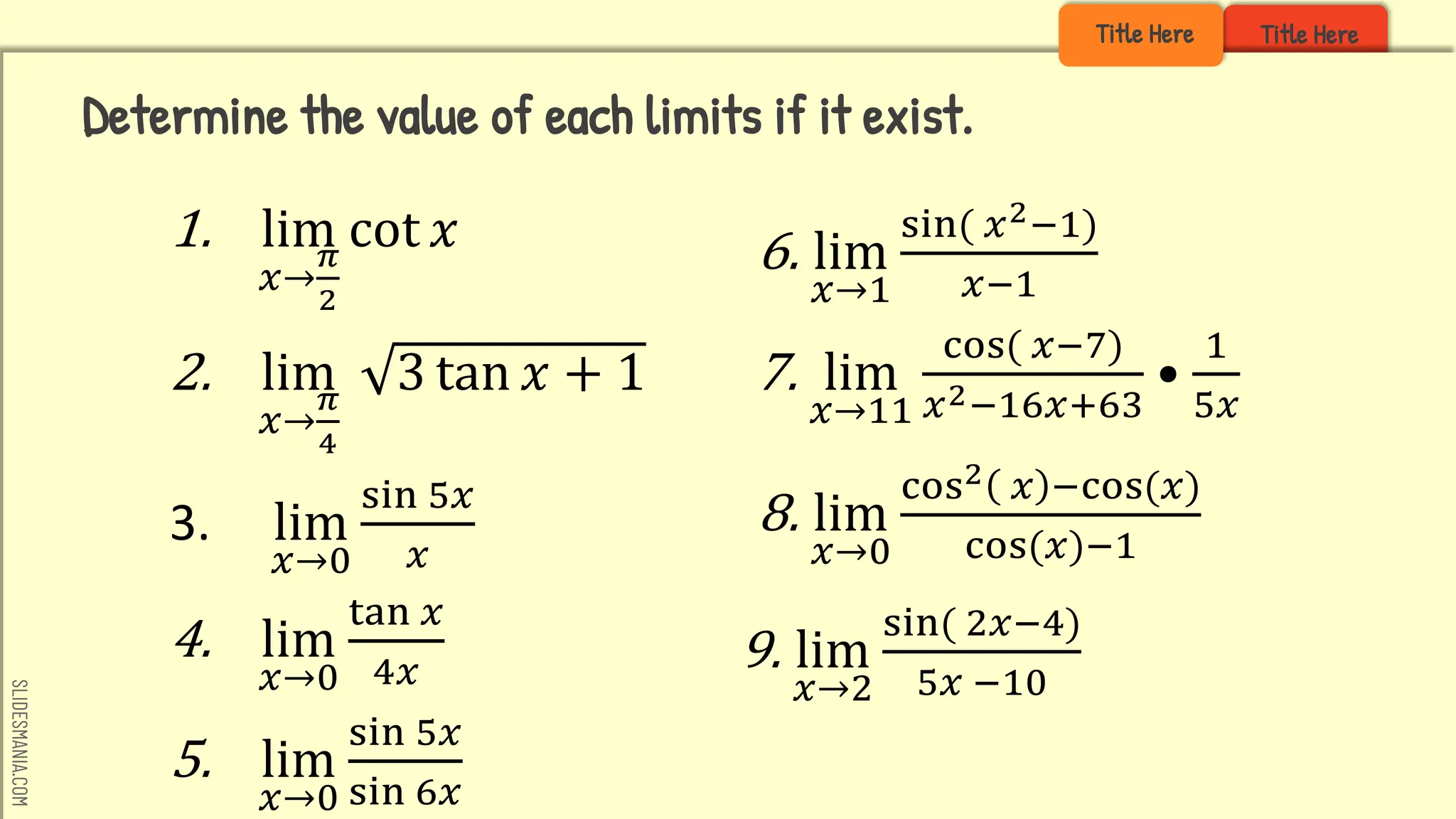The document covers the evaluation of limits involving trigonometric functions, stating key limits and techniques to find them. It provides several examples to demonstrate understanding, including limits as x approaches specific values. Resources and references for further study on trigonometric limits are also included.



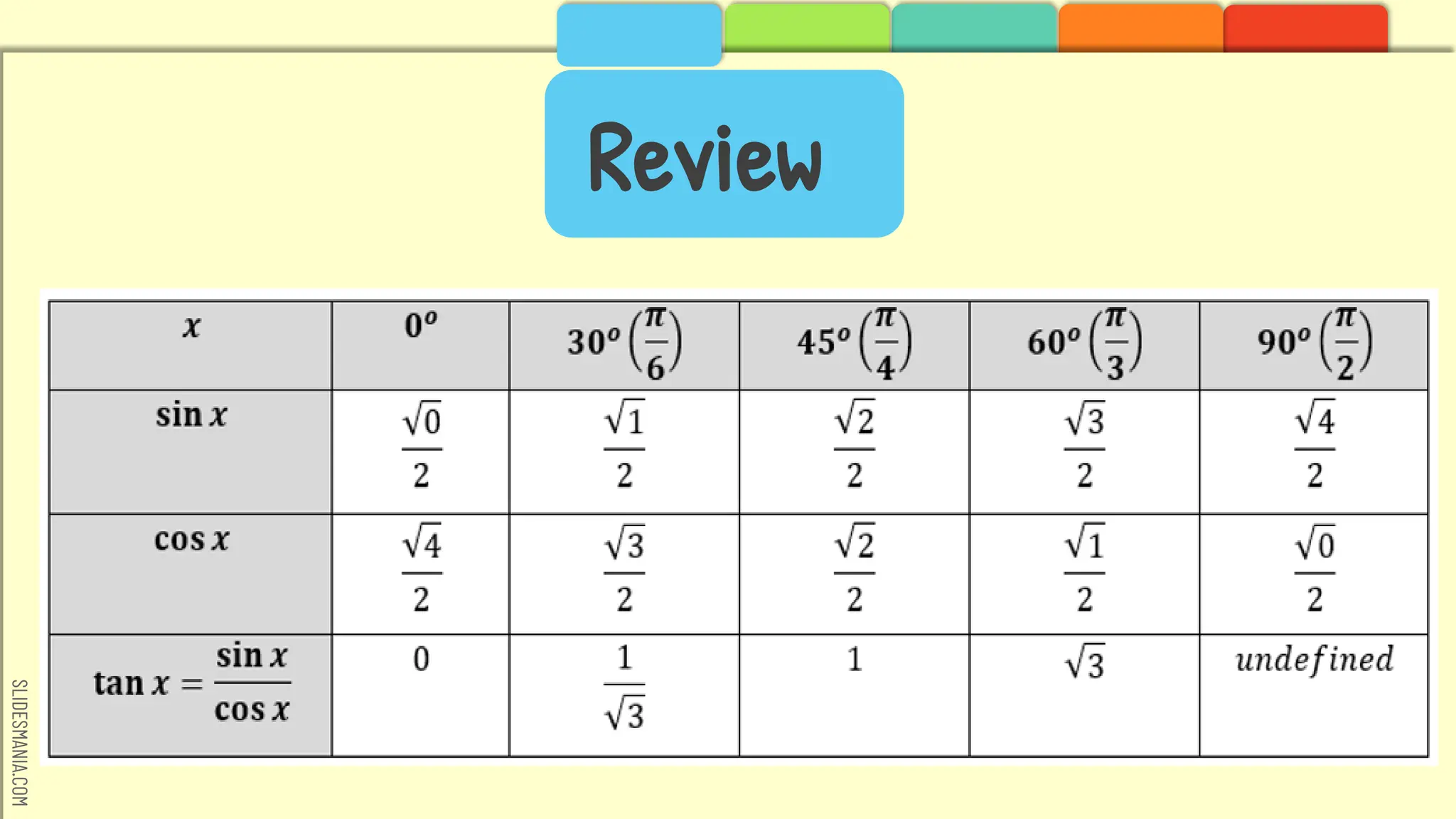


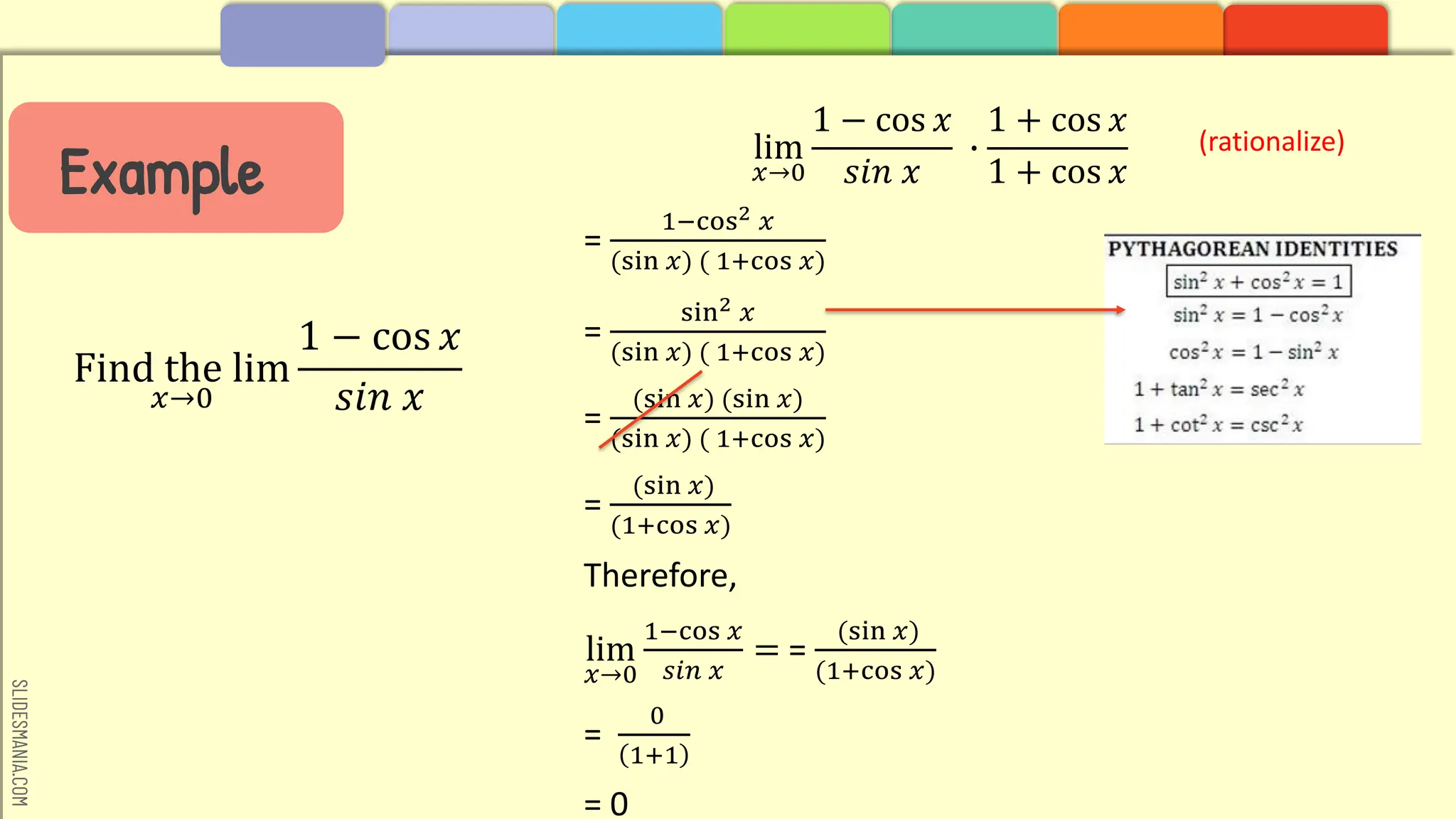



![SLIDESMANIA.COM
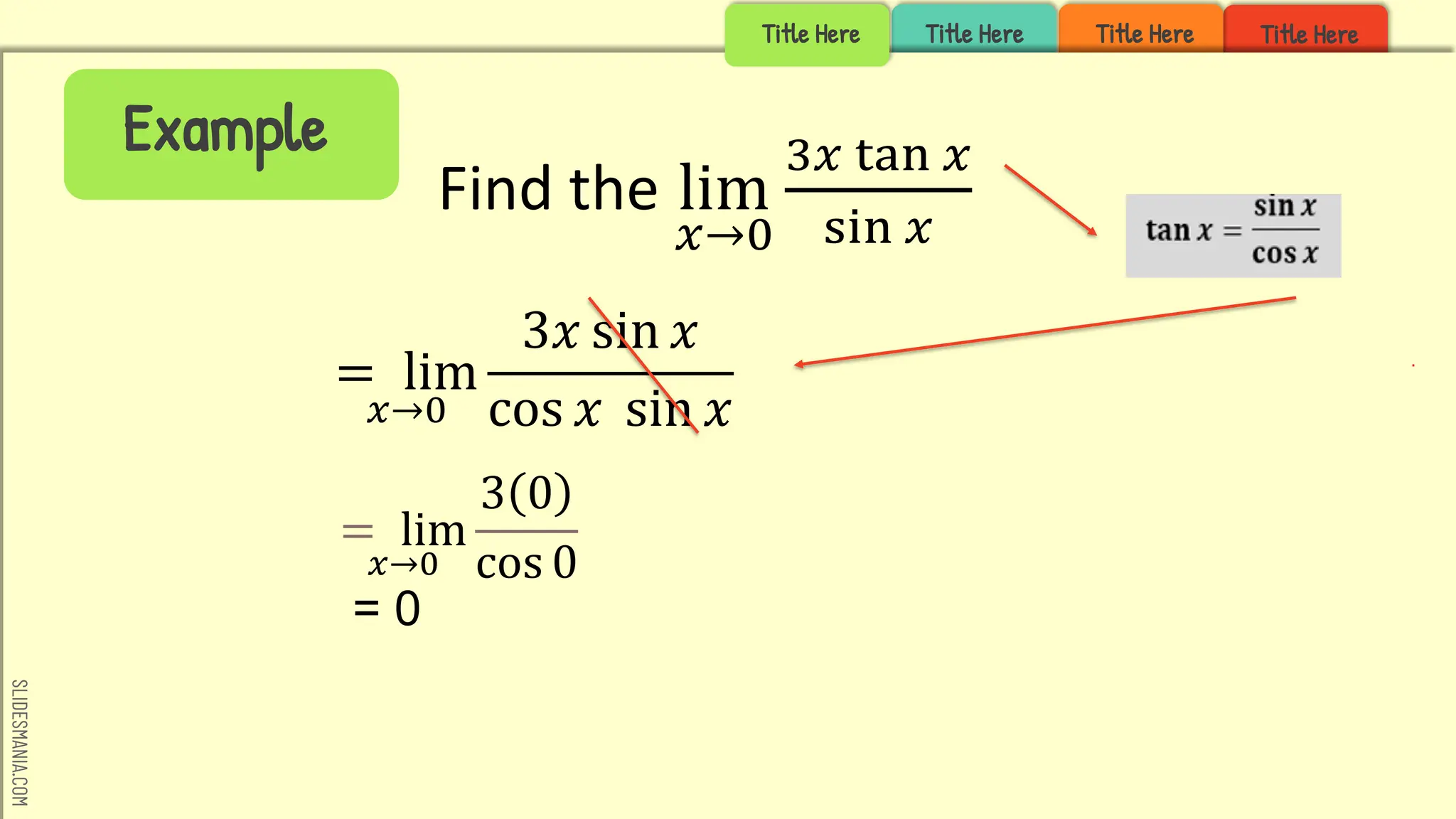
Example
lim
ℎ→
𝜋
4
8𝑥 tan 𝑥 − 2𝜋 tan 𝑥
4𝑥 − 𝜋
= lim
ℎ→
𝜋
4
2 tan 𝑥 [ 4𝑥−𝜋]
4𝑥− 𝜋
lim
ℎ→
𝜋
4
2 tan 𝑥 [ 4𝑥−𝜋]
4𝑥− 𝜋
( 𝑎𝑝𝑝𝑙𝑦𝑖𝑛𝑔𝑓𝑎𝑐𝑡𝑜𝑟𝑖𝑛𝑔 𝑐𝑜𝑚𝑚𝑜𝑛 𝑚𝑜𝑛𝑜𝑚𝑖𝑎𝑙 𝑓𝑎𝑐𝑡𝑜𝑟)
= lim
ℎ→
𝜋
4
2 tan 𝑥
= 2tan
𝜋
4
= 2 (1)](https://image.slidesharecdn.com/limits-involving-trigonometric-functions-241123125902-87a6a031/75/Limits-Involving-Trigonometric-Functions-pdf-12-2048.jpg)