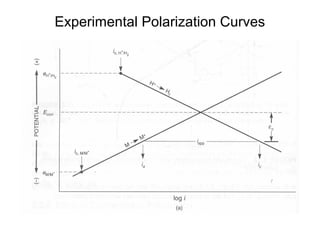
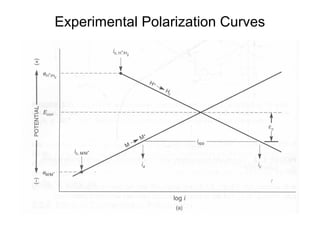
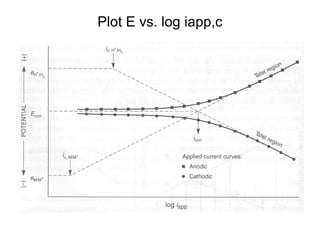
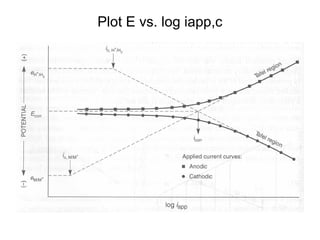
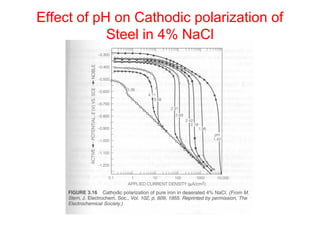
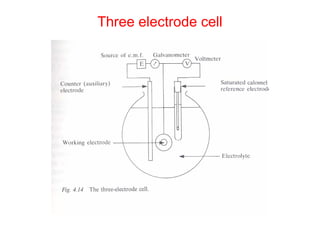
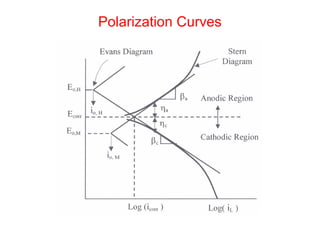
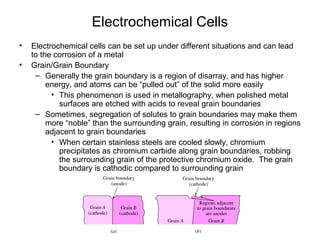
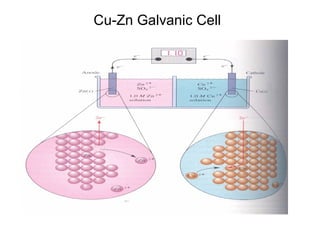
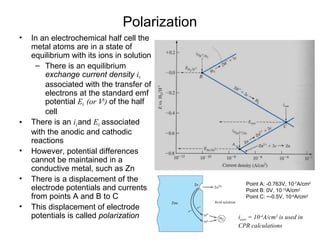
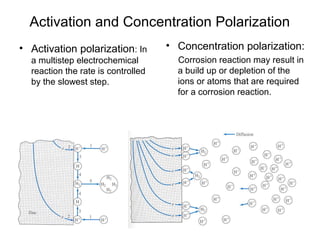
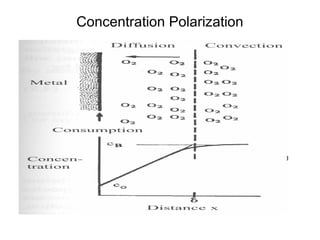
This document summarizes lecture material on corrosion kinetics. It discusses various types of electrochemical cells that can lead to corrosion, including grain boundaries and multiphase materials. It also covers polarization, passivation, galvanic series, corrosion rates, concentration polarization, and experimental polarization curves. Key points include how concentration gradients can limit corrosion current and affect polarization, and how polarization curves are used to determine corrosion kinetics parameters.

1. Lecture:3
Corrosion Kinetics
Asst. Prof. Dr. Ali Sabea Hammood
Materials Engineering Department
Faculty of Engineering-University of Kufa
IRAQ

2. Electrochemical Cells
• Electrochemical cells can be set up under different situations and can lead
to the corrosion of a metal
• Grain/Grain Boundary
– Generally the grain boundary is a region of disarray, and has higher
energy, and atoms can be “pulled out” of the solid more easily
• This phenomenon is used in metallography, when polished metal
surfaces are etched with acids to reveal grain boundaries
– Sometimes, segregation of solutes to grain boundaries may make them
more “noble” than the surrounding grain, resulting in corrosion in regions
adjacent to grain boundaries
• When certain stainless steels are cooled slowly, chromium
precipitates as chromium carbide along grain boundaries, robbing
the surrounding grain of the protective chromium oxide. The grain
boundary is cathodic compared to surrounding grain

3. Electrochemical Cells
• In multiphase materials, one phase may be anodic with respect to
another
– Corrosion rates are higher in multiphase materials.
– For example
• In pearlitic gray cast iron, graphite is more noble than
pearlite, leading to corrosion of pearlitic regions
• Martensite (single phase) is more corrosion resistant than
austenite that has been slow cooled to form pearlite (two
phase)
• Tempered martensite corrodes more easily than martensite
– Low temperature tempering results in finer Fe3C particles and
more corrosion sites
– Higher temperature tempering results in coarser Fe3C particles
and fewer corrosion sites

4. Cu-Zn Galvanic Cell

5. Cu-Zn Galvanic Cell
• C: (Cu+2+2e-↔Cu)
• A:(Zn↔Zn+2+ 2e-)
• Overall reaction is the addition of A and C
• Cu+2+ Zn→Cu + Zn+2
• The reversible cell potential is 1.1 V (net current = 0)•
• The maximum work done by the battery is
• (ΔGcell= -n*F*Ecell)
• ΔGcell= -2*96500*1.1= -212.300 KJ

7. Corrosion Kinetics
• Up to this point, we have dealt
with the thermodynamics of
corrosion, i.e. which combinations
of conditions results in anodic and
cathodic regions under equilibrium
• Corrosion does not occur under
equilibrium conditions
• Of interest is the corrosion
kinetics, i.e. the rate at which a
metal corrodes
• For each atom of a metal that
participates in the oxidation
reaction, n electrons need to get
transported away
• The weight of a metal that is lost
due to corrosion is given by
Faraday’s law
• M  Mn+
+ ne-
w = weight loss during corrosion (or
weight gain during electroplating)
I = current in amps = iA
i = current density
A = area of corroding surface
t = time in seconds
M = atomic mass g/mole
n = number of electrons involved in the
corrosion reaction
F = Faraday’s constant
= 96,500 C/mol
nF
ItM
w =

8. Polarization
• In an electrochemical half cell the
metal atoms are in a state of
equilibrium with its ions in solution
– There is an equilibrium
exchange current density i0
associated with the transfer of
electrons at the standard emf
potential E0 (or V0
) of the half
cell
• There is an i0 and E0 associated
with the anodic and cathodic
reactions
• However, potential differences
cannot be maintained in a
conductive metal, such as Zn
• There is a displacement of the
electrode potentials and currents
from points A and B to C
• This displacement of electrode
potentials is called polarization
Point A: -0.763V, 10-7
A/cm2
Point B: 0V, 10-10
A/cm2
Point C: ~-0.5V, 10-4
A/cm2
icorr = 10-4
A/cm2
is used in
CPR calculations

9. Activation and Concentration Polarization
• Activation polarization: In
a multistep electrochemical
reaction the rate is controlled
by the slowest step.
• Concentration polarization:
Corrosion reaction may result in
a build up or depletion of the
ions or atoms that are required
for a corrosion reaction.

11. Concentration Polarization
• Cations involved in cathodic reactions are depleted near
the cathode at high currents such as a metal ion
reduction reaction:
• M+n+ ne-→M.
• •For example, the figure shows the oxygen concentration
as a function of the distance from the electrode surface
submerged in an aerated solution and the main
reduction is reaction is:
• O2+ 2H2O + 4e-→4OH-
• •The ions concentration near the surface depends on
ions diffusion.

12. Concentration Polarization

13. Concentration Polarization

14. Concentration Polarization
• The concentration of the cations will vary from near the
surface concentration (Cs) to the bulk concentration
• (CB)across the cathode over a distance (δ):
• –Concentration gradient = dC/dx= (CB -Cs)/δ

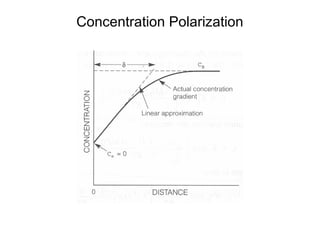
15. Concentration Polarization
• M+n+ ne-→M
• •Before current flow:
• –ei=eo+ 2.3RT/nF log ([CB]/1)
• •After current flow:
• –ef=eo+ 2.3RT/nF log ([Cs]/1)
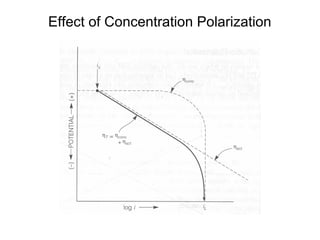
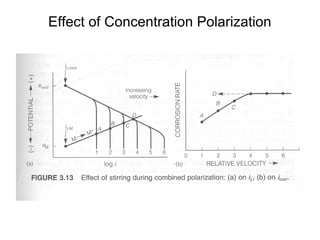
• •Concentration cathodic overpotential = ηc,conc
• •= ef-ei= 2.3RT/nF*log (Cs/CB)
• •Cs= CB-icδ/(nFDions)
• •CB= iLδ/(nFDions)
• •ηc,conc= 2.3RT/nF Log {1-(ic/il) }
• –If ic<<il, then ic/il→0 and ηc,conc= 2.3RT/nF log (1) = 0
• –If ic≈il, then ic/il→1 and ηc,conc= 2.3RT/nF log (0) = -∞

16. Concentration Polarization
• J = D ions dC /dx= D ions (CB -Cs)/δ
• Cathodic current = n F*J=n F D ions(CB-Cs)/δ
• Maximum current when Cs=0 ,
• The maximum cathodic current:
• –ic, max= iL= n F Dions CB/δ
• This is called the limiting current density

17. Concentration Polarization

18. Concentration Polarization
• ηc,conc= 2.3RT/nF Log {1-(ic/i) }
• –If ic<<il, then ic/il→0 and ηc,conc= 2.3RT/nF log (1) = 0
• –If ic≈il, then ic/il→1 and ηc,conc= 2.3RT/nF log (0)
• = -∞

19. Concentration Polarization

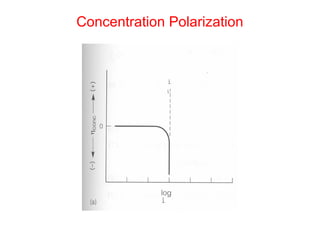
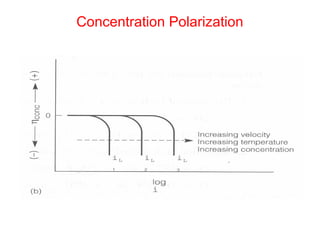
20. Concentration Polarization
• Q: Estimate iL at 298 K for copper
reduction reaction with bulk concentration
of [Cu++] = 0.1 M in unstirred solution
where δ=0.3 mm. DCu++= 7x10-10m2/s
• •iL= nFDionsCB/δ= 2*96500* 7x10-
100.1/0.0003 = 4.58 mA/cm2

21. Concentration Polarization
• iL= nFDionsCB/δ
• –nFDionsCB= constant at a given temperature.
• –δis the diffusion boundary layer thickness.
• –iLcan be increased by decreasing δ
• –δcan be decreased by stirring the solution.

22. Passivation
• Passivation is the loss of chemical reactivity in presence
of a environmental condition.
– The formation of surface layer of reaction products that inhibit
further reaction
• Oxide film theory: A passive film of reaction products
acts as a diffusion barrier.
• Adsorption theory: Passive metals are covered by
chemisorbed films of oxygen.
• Examples: Stainless steel, nickel alloys, titanium and
aluminum alloys passivate in certain environments

23. Polarization Curve for Passivation
• Initially, the potential of the metal increases with current density, i.e. the
metal undergoes active corrosion
• When potential reaches Epp the primary passive potential, current density
decreases, i.e., the corrosion rate also decreases
• In order to make the metal active again, there may need to be an
externally applied potential

24. Galvanic Series
• The Standard emf series gives
the relative oxidation or
reduction behavior under
standard conditions.
• The Galvanic series ranks
materials on the basis of
corrosion behavior in sea
water

25. Corrosion Rates
• P.R. = 0.129 i* AW/ n D
• The term AW/n is called the equivalent weight (EW) and
is useful when dealing with alloys.
• The alloy EW is the weighted average of AW/n for all
major alloying elements in the alloy.
• NEQ= Σ(fi/( Awi / ni )= Σ( fi ni / Awi )= where f is the
mass fraction of the element in the alloy
• EW = 1/ NEQ

26. • The acceptable corrosion rates depends greatly on the
dimensional tolerance of the component. Corrosion
resistance alloys:
• –< 0.1 mm/y is excellent corrosion resistance
• –0.1-1 mm/y intermediate corrosion resistance
• –>1 mm/y low corrosion resistance
• •For example, Saudi Aramcohas criteria for corrosion
rates in pipes:
• •an acceptable corrosion rate is <0.1 mm/y
• •Severe corrosion is > 0.5 mm/y
• •Note that the acceptable corrosion rates depends
greatly on the dimensional tolerance of the corroding
component:
• –0.4 mm/y could be acceptable for large pipes
• –0.01 mm/y not acceptable for rotating machinery
bearings

27. Corrosion Rates
• Calculate the EW for 304 stainless steel (71.75%Fe,
19%Cr, 9.25%Ni)
• NEQ= Σ(fini/AWi)
• = 0.7175*2/55.85+ 0.19*3/52+0.0925*2/58.71= 0.03981
• EW = 1/ NEQ= 1/0.03981= 25.12
• …………………………………………………………………
• Example: what is the penetration rate for stainless steel
if i= 0.001 mA/cm2.
• P.R. = 0.00327 i*EW/D
• P.R. = 0.00327*1*25.12/7.9 = 0.02 mm/y

28. Cathodic Tafel Constants

29. Zn in acid solution

30. Zn in acid solution

31. Zn in acid solution

32. Fe in acid solution

33. Effect of added oxidizer

34. Effect of Concentration Polarization

35. Effect of Concentration Polarization
• Assume the cathode is under
both activation and concentration
polarization
• •icorr= iL

36. Effect of Concentration Polarization

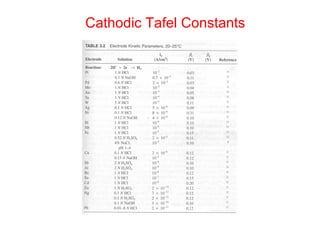
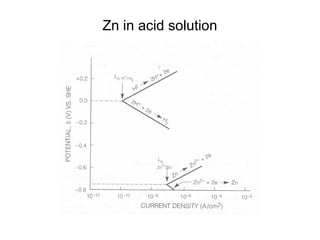
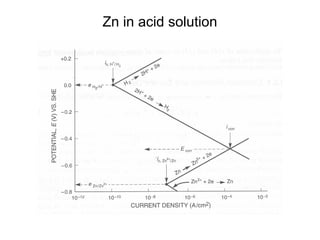
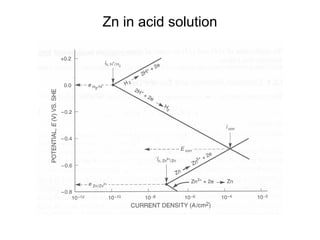
37. Example:
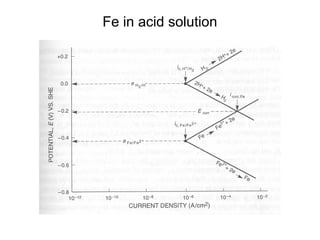
• Q: Estimate the corrosion rate, penetration rate, and
Ecorrfor a Zn tank containing oxygen free solution
(pH=0). Assume both anodic and cathodic reactions are
under activation control. [Zn++] = 1 M at 298 K.
• •io, Zn= 1x10-7A/cm2, βa= 0.09 V/decade
• •io, H= 1x10-10A/cm2 , βc= -0.08 V/decade

38. Results
• icorr= 1.2x10-4A/cm2= 120 μA/cm2
• •r= i*AW/nF= 1.2x10-4(A/cm2)*65.4g/mol/(2*96500
coulomb)
• •r= 4x10-8g/(cm2*s)
• •P.R.=0.00327 i( in μA/cm2)*AW/nD
• •P.R.=0.00327*120 (μA/cm2)*65.4/(2*7.13 g/mol) = 1.8
mm/y
• •Ecorr= ηclog (ic/io,c) = -0.08 log(1.2x10-4/ 1x10-10)=-
0.486V

39. Questions:
• For the same problem, assume that the limiting
current density for hydrogen reduction on Zn is
5x10-5A/cm2.
• What is icorr and Ecorr. •
• Since iL< 1.2x10-4A/cm2•icorrwill be limited by
iL•
• icorr= 5x10-5A/cm2•
• P.R. = 0.75 mm/yr•
• Ecorr= 0.09Log•(5x10-5/1x10-7)-0.76=-0.52V

40. Questions:

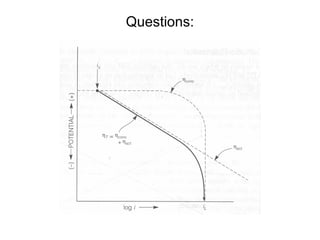
41. Questions:
• Estimate the corrosion rate, penetration rate, and
Ecorrfor steel tank containing aerated acid (pH=2).
Assume both anodic and cathodic reactions are under
activation control. [Fe++] = 0.1 M at 298 K.
• •io, Fe= 1x10-6A/cm2, βa= 0.1 V/decade
• •io, H= 1x10-5A/cm2 , βc= -0.1 V/decade

42. Experimental Polarization Curves
• Mixed potential theory was proposed to explain
experimentally measured polarization curves.
• •We want to measure the polarization curves for a metal
M in acid solution:
• –anode half-cell reaction is M↔M+n+ ne-
• –cathode half-cell reaction is H++ 2e-↔H2
• •From the polarization curves:
• –we can get Tafel constants for the reactions to estimate
corrosion rates.

43. Experimental Polarization Curves
• Potential and current initially at Ecorr and at icorr
• at “free corrosion condition”
• •Forced polarization in the cathodic direction using
external current.
• –iapp,c: electrons are supplied to the electrode
• –εc= (E-Ecorr) cathodic overpotential from
• Ecorr(-ve overpotential)
• –ηc= (E-e) cathodic overpotential from half-cell
reversible potential ηc icorr

44. Experimental Polarization Curves

45. Experimental Polarization Curves
• Both the anodic and cathodic reactions are at a common
potential E
• –The anodic reaction current is decreased from I corr
• to Ia
• –The cathodic reaction current is increased from I corr
• to Ic
• –I app,c = Ic–Ia
• –Plot E vs. log Iapp,

46. Experimental Polarization Curves

47. Plot E vs. log I app,c
At low εc (small difference between E and
Ecorr)
–iapp,c = ic–ia ( ic is slightly greater than ia )
and iapp,c is very small
–Note that the dashed lines are theoretical

48. Plot E vs. log iapp,c

49. Plot E vs. log iapp,c

50. Steel in Acid Solution

51. Effect of pH on Cathodic polarization of
Steel in 4% NaCl

52. Three electrode cell

53. Three electrode cell
• For this purpose, we use a potentiostat.
• •A potentiostat: an equipment that supplies whatever
current needed between working and counter electrodes
to maintain specific potential between working and
reference electrode
• –Independent variable (you can set): the potential
• –Dependent variable: the current
• •NOTE:
• –Almost all current flows between the working and the
counter electrodes
• –The potential is measured between the working and the
reference electrode.

54. Polarization Curves

55. References:
• 1- L. Shreir, Corrosion- Volume 1: Metal Environment
Reactions, Newnes – Butter wroths, 1976.
• 2- U. R. Evans, The Corrosion and Oxidation of Metals:
Scientific Principles and Practical Applications, Edward
Arnold, 1981, pp. 360-392.
• 3- J. C. Scully, The Fundamentals of Corrosion, Third
Edition, Pergamon Press, 1990.
• 4- M. G. Fontana, N. D. Greene, Corrosion Engineering,
Second Edition, McGraw – Hill, 1986.

56. References:
• 5- P. R. Roberge, Corrosion, Engineering, Principle&
Practice McGraw Hill,2008.
• 6- W. H. Ailor, Handbook on Corrosion Testing and
Evaluation, The Electrochemical Society, John Wiley and
sons, 1971.
• 7- K. R. Trethewey, and J. Chamberlain, Corrosion for
Science and Engineering, Longman, 1995.
• 8-Zaki Ahmed, Principles of corrosion engineering and
corrosion control, First Edition, BH, 2006.