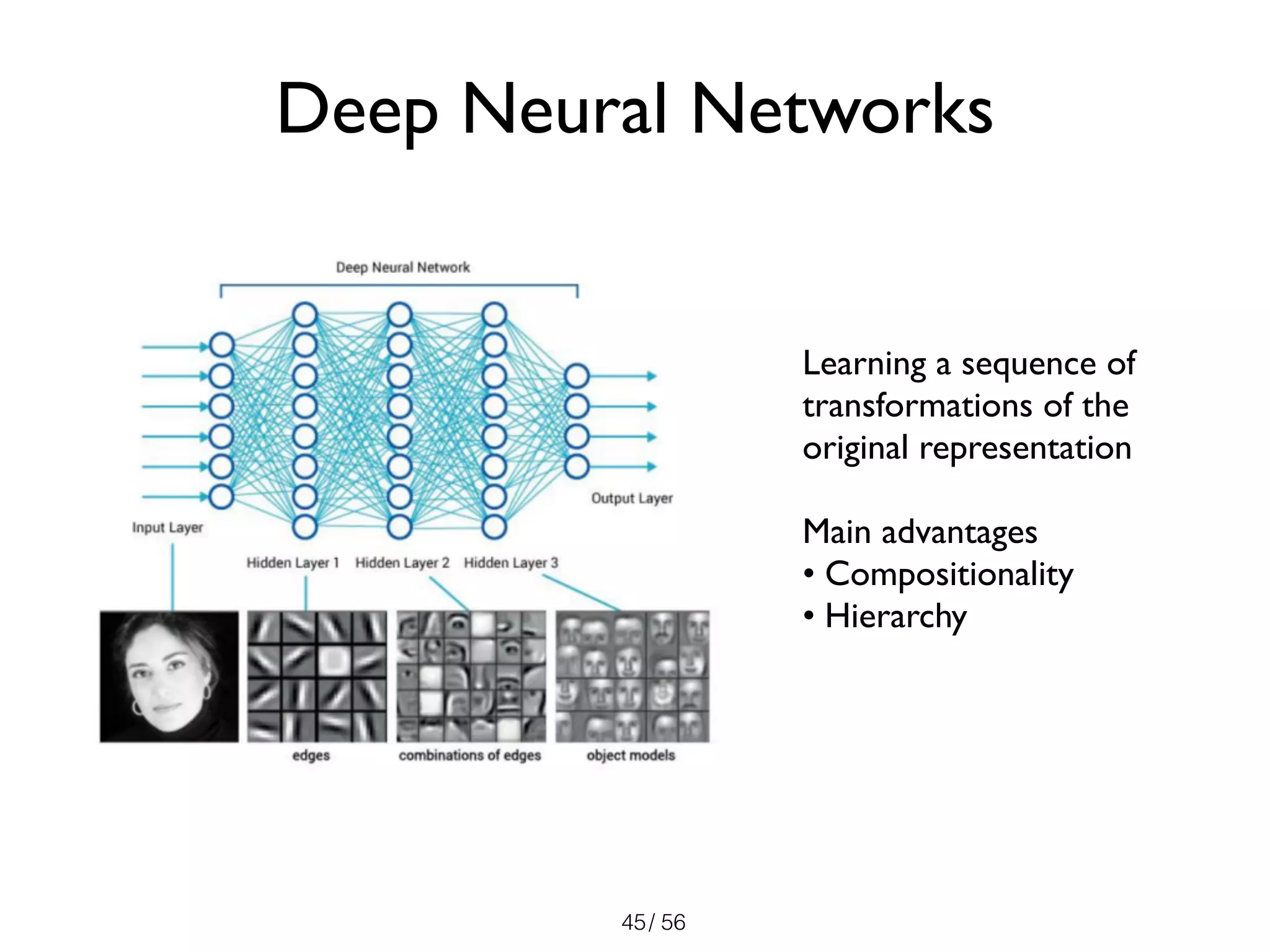
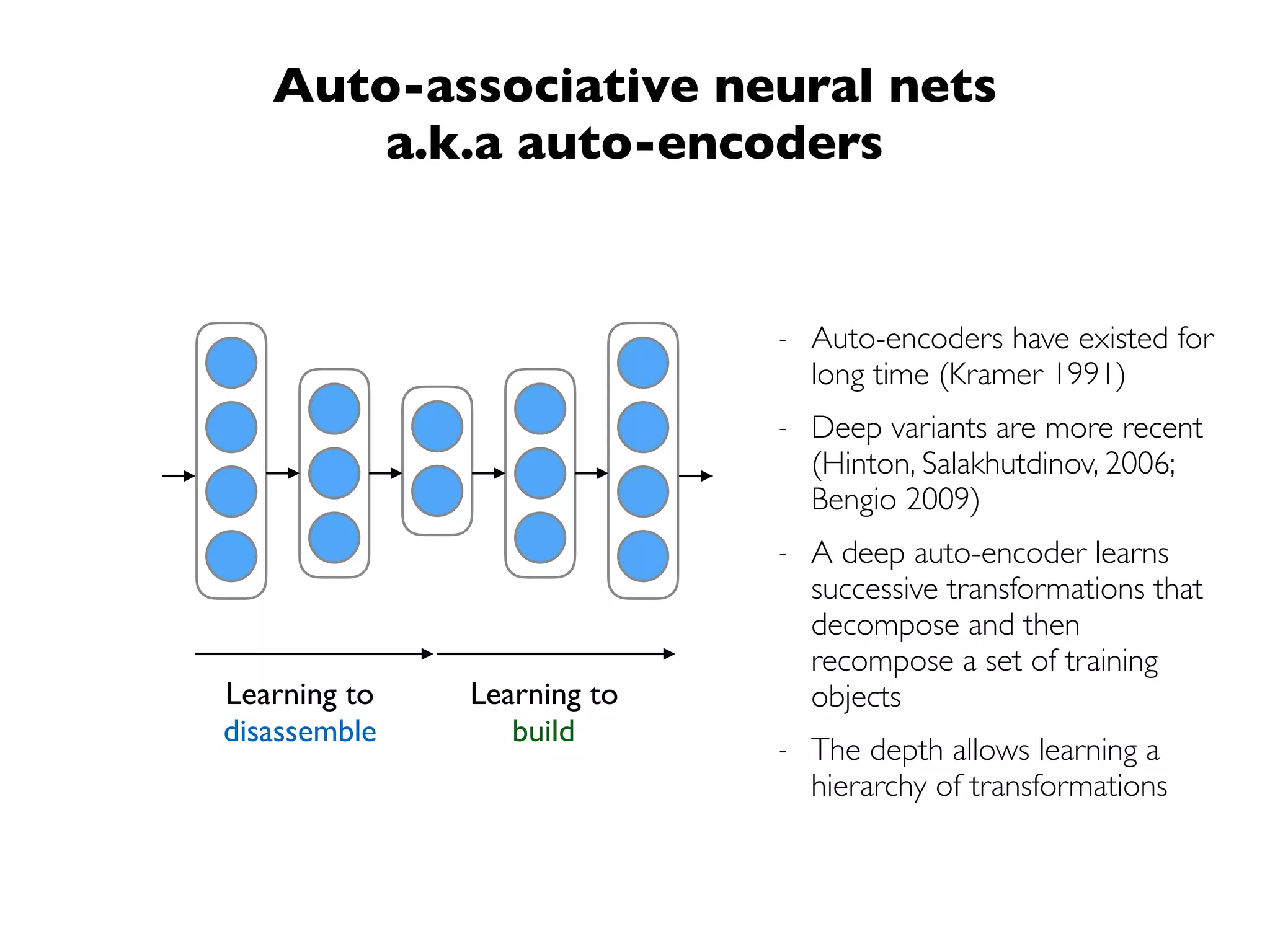
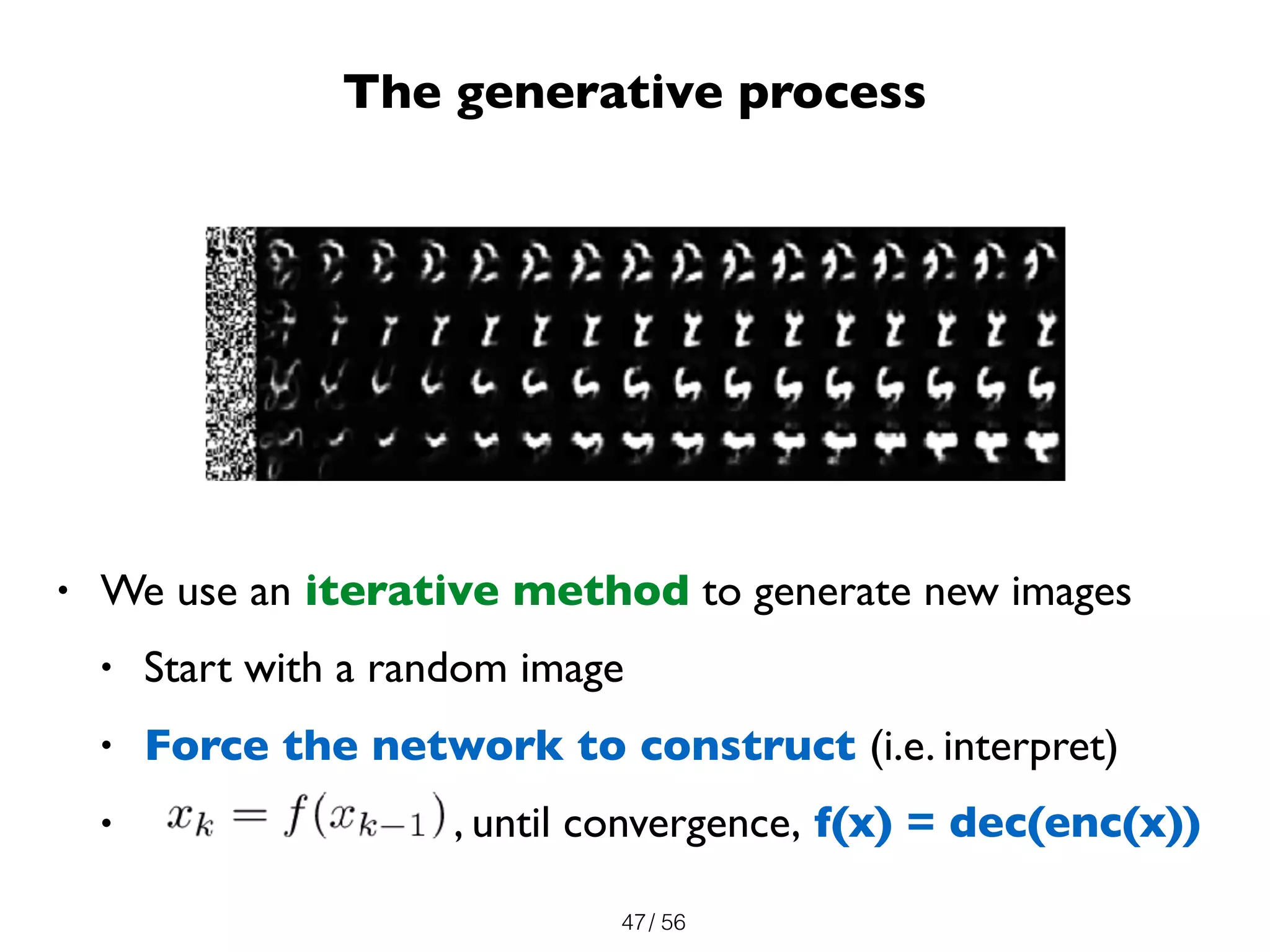
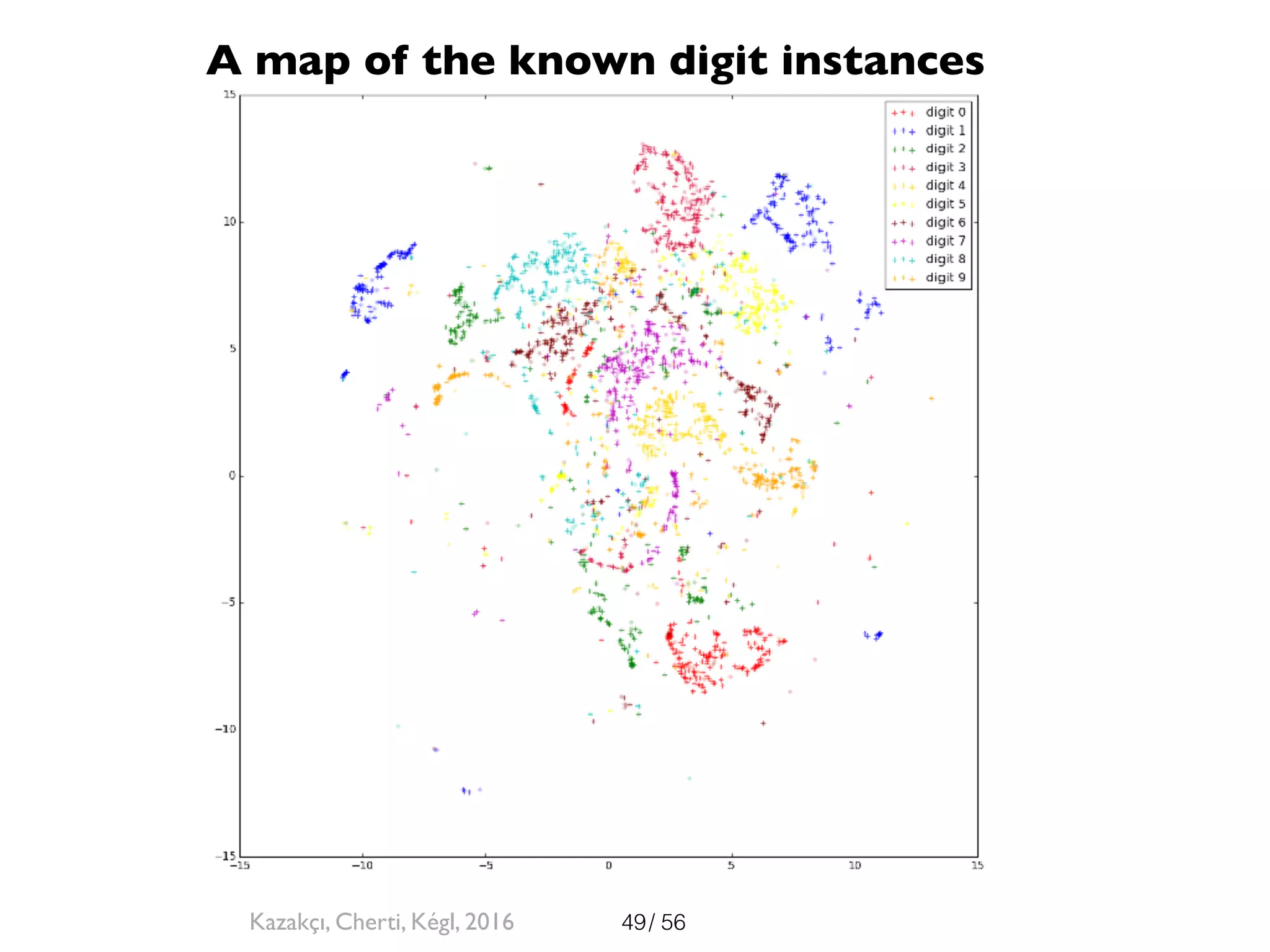
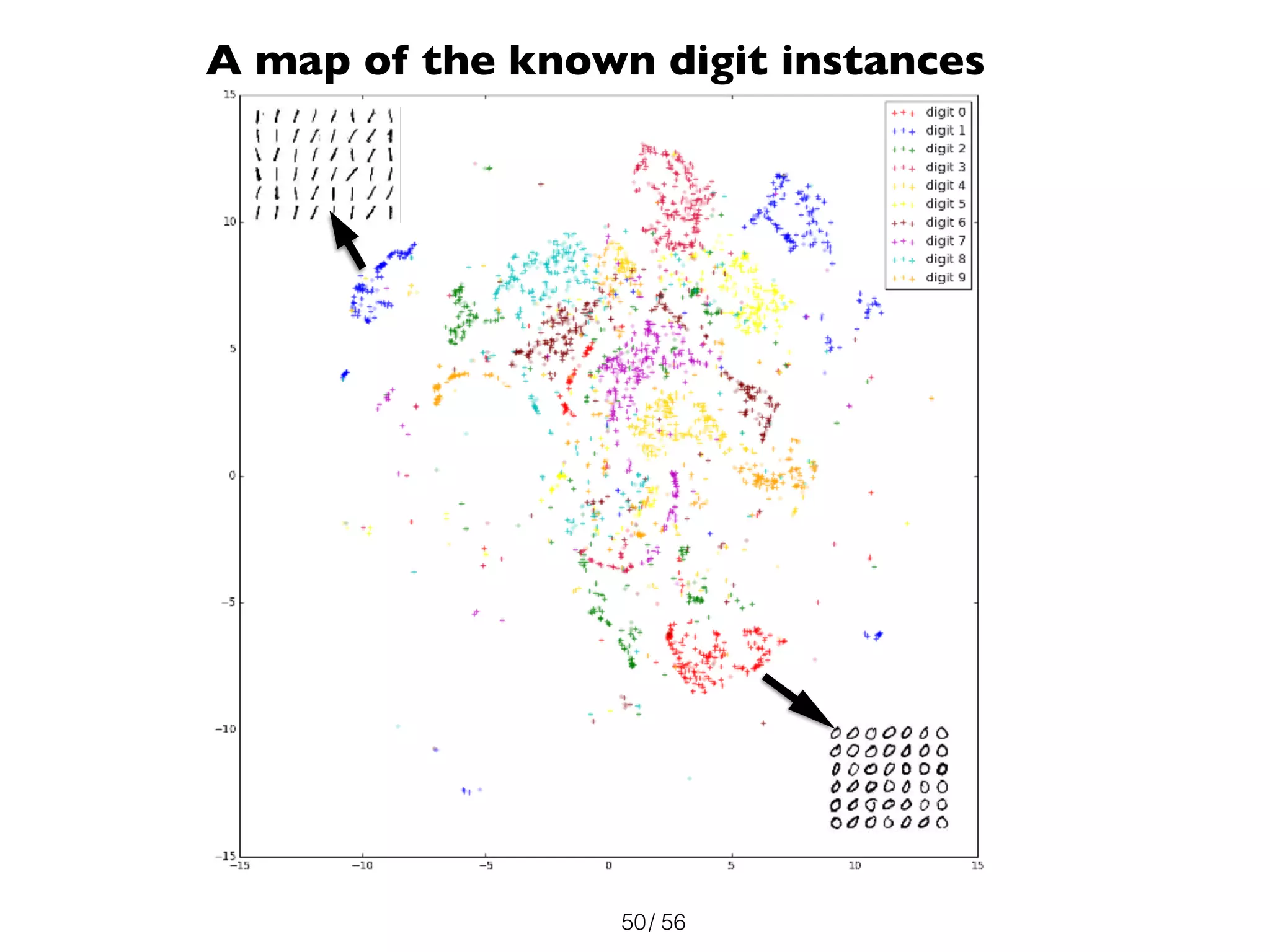
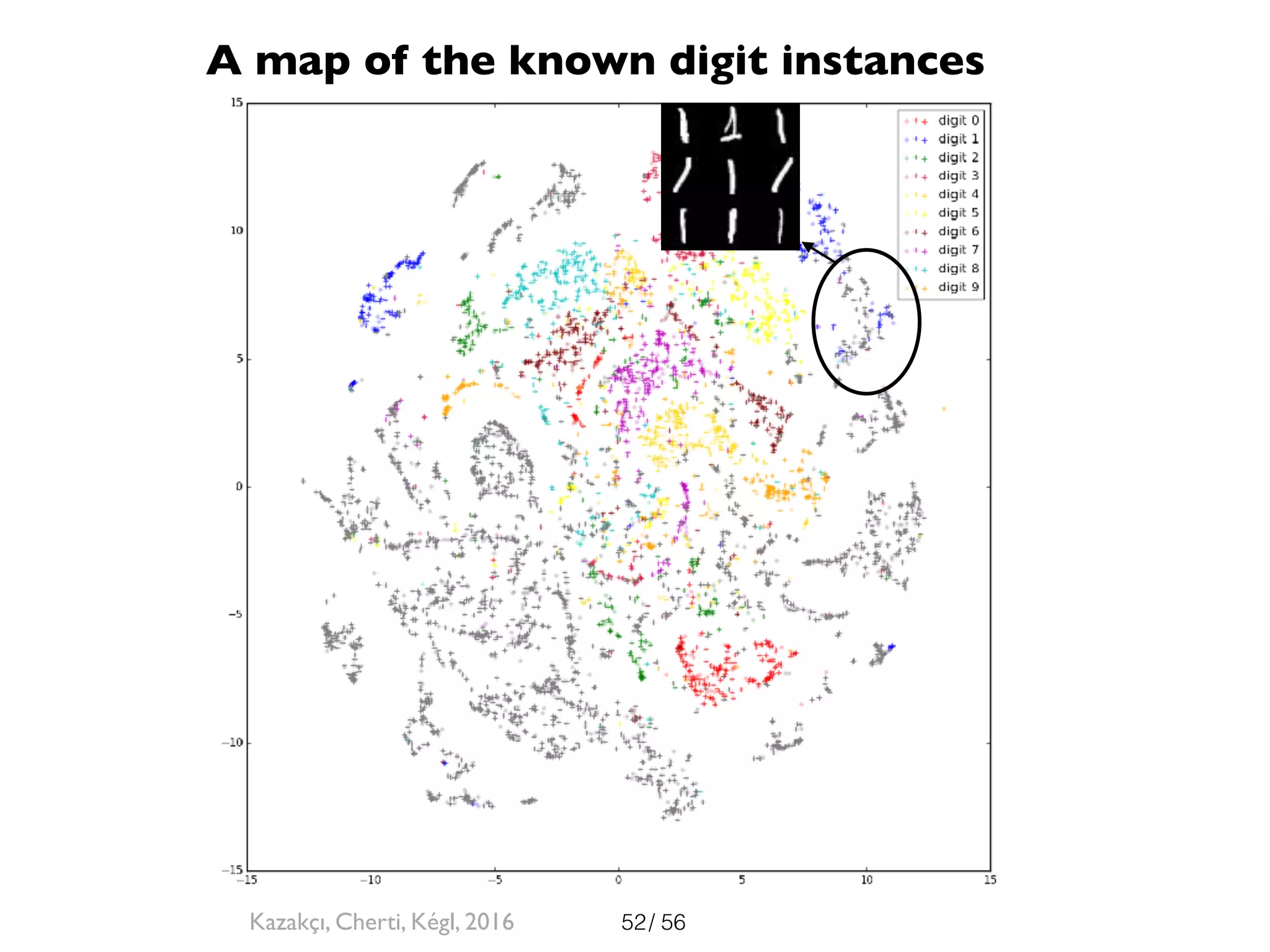
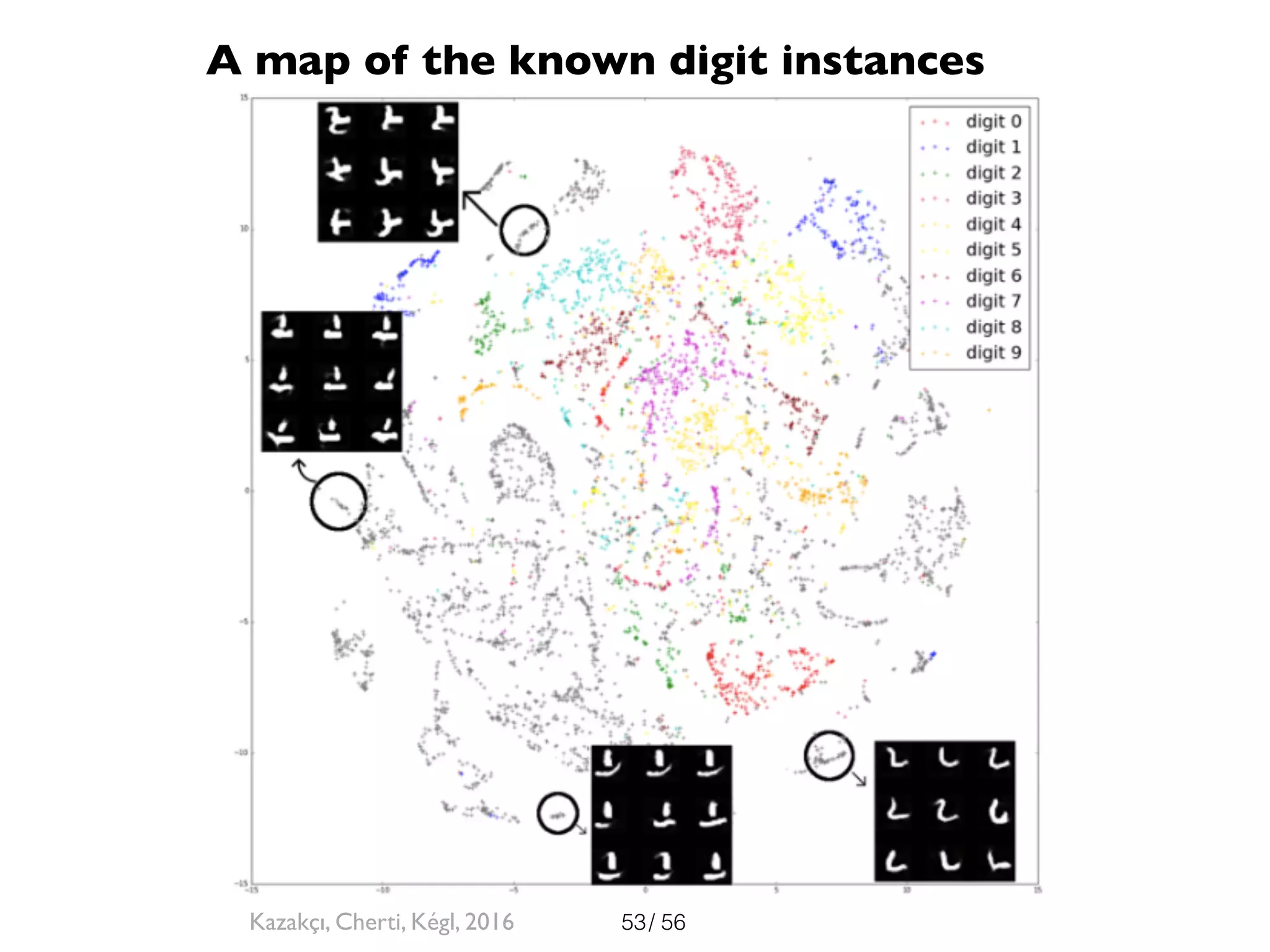
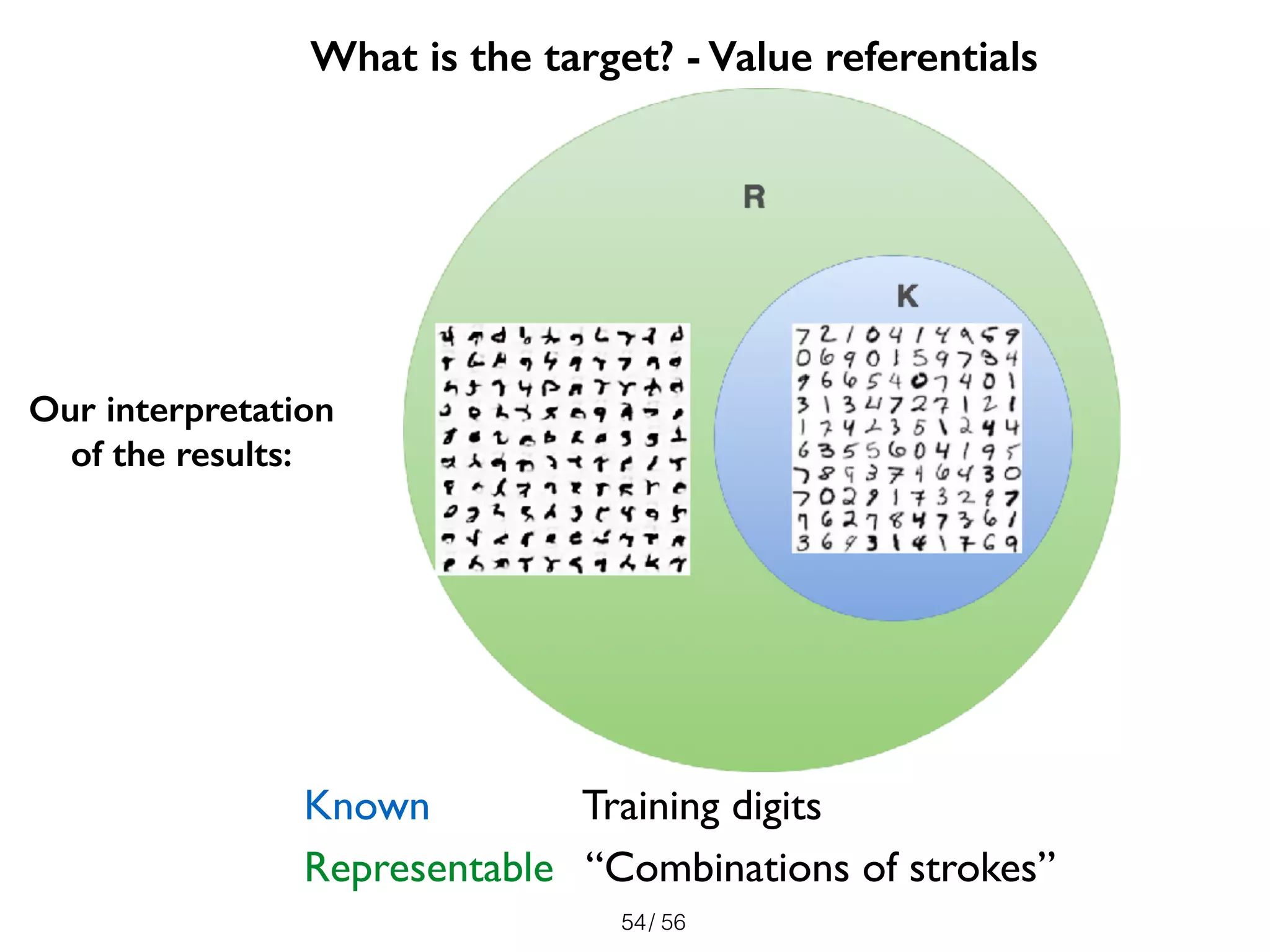
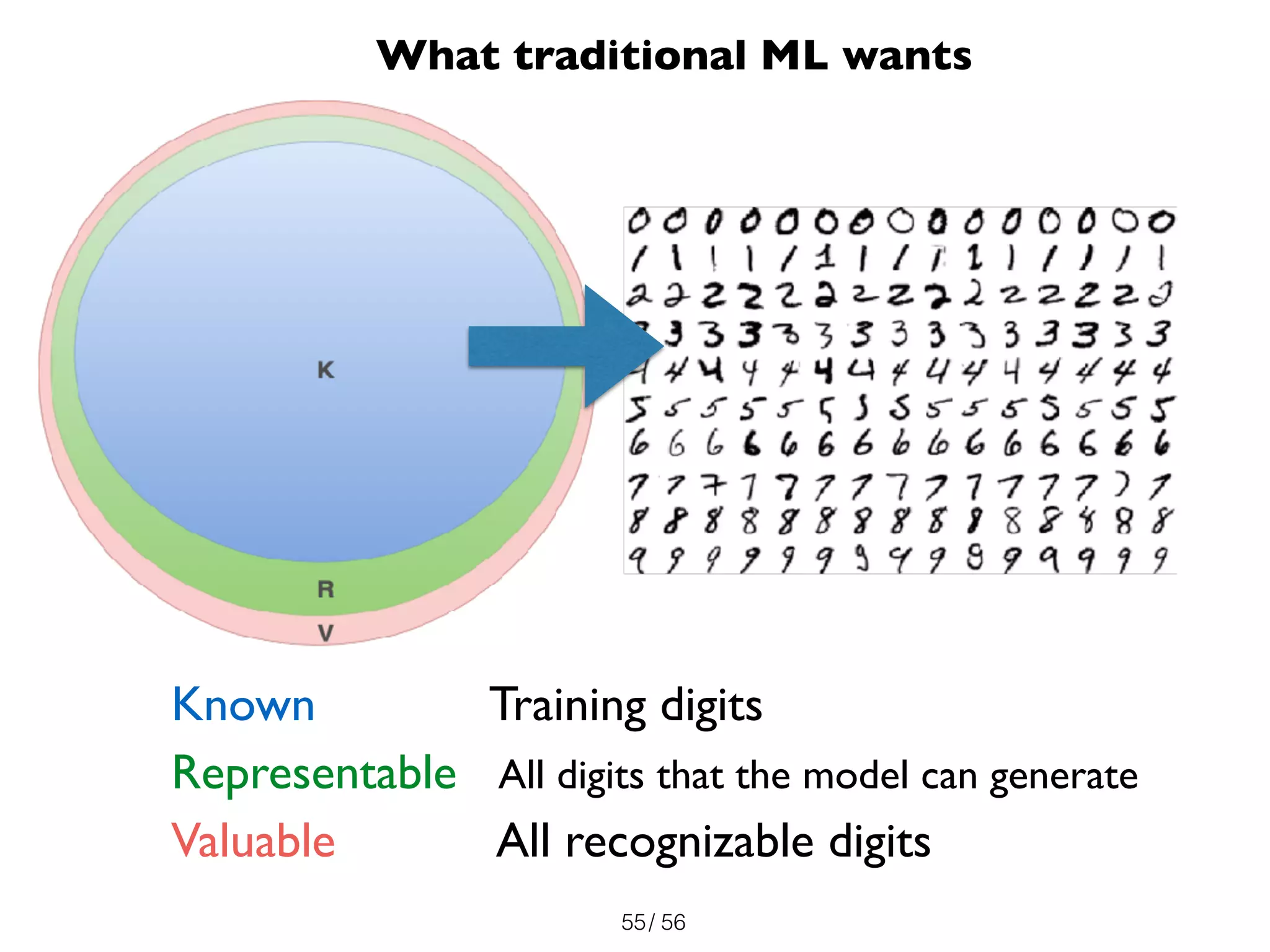
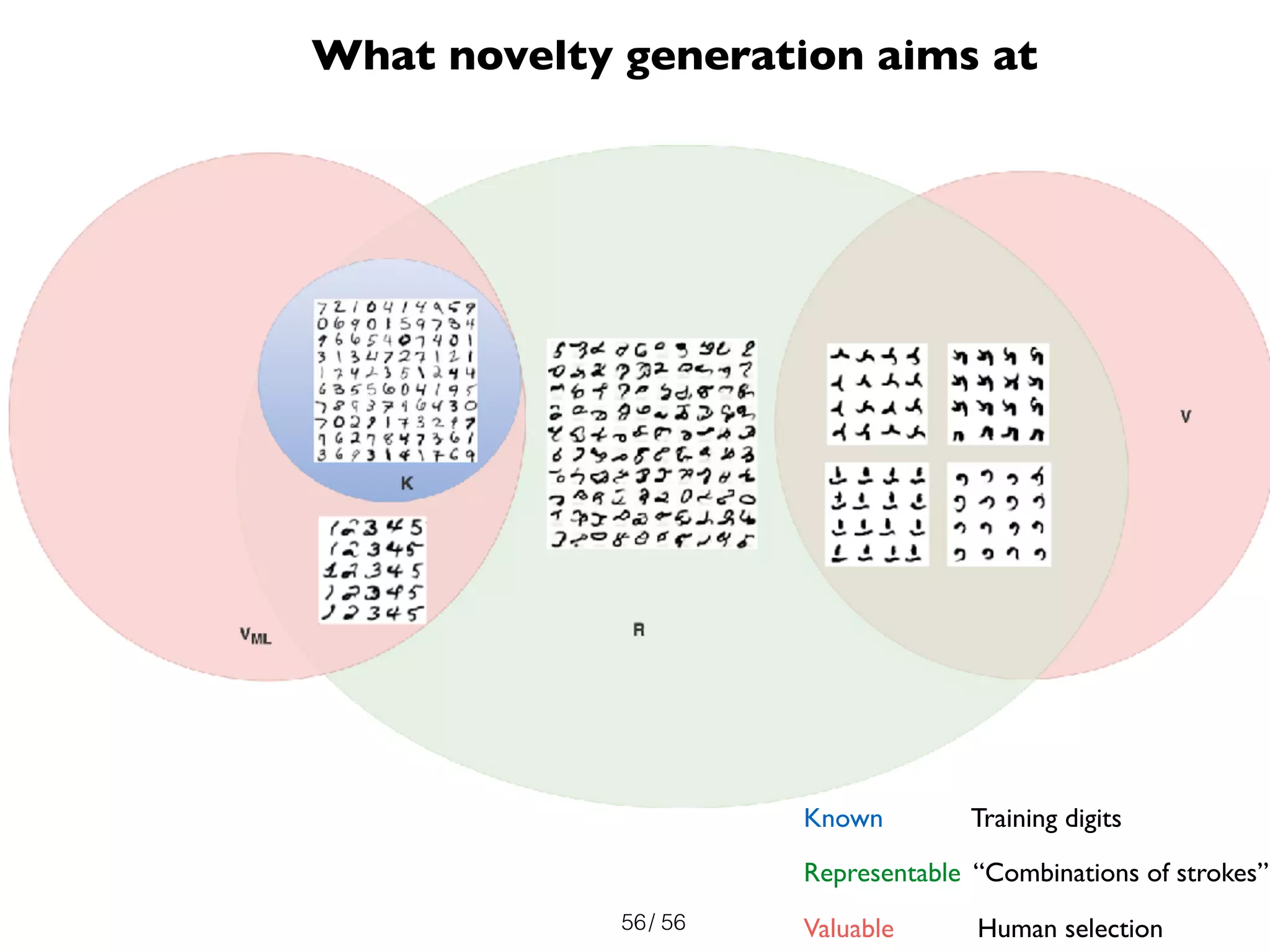
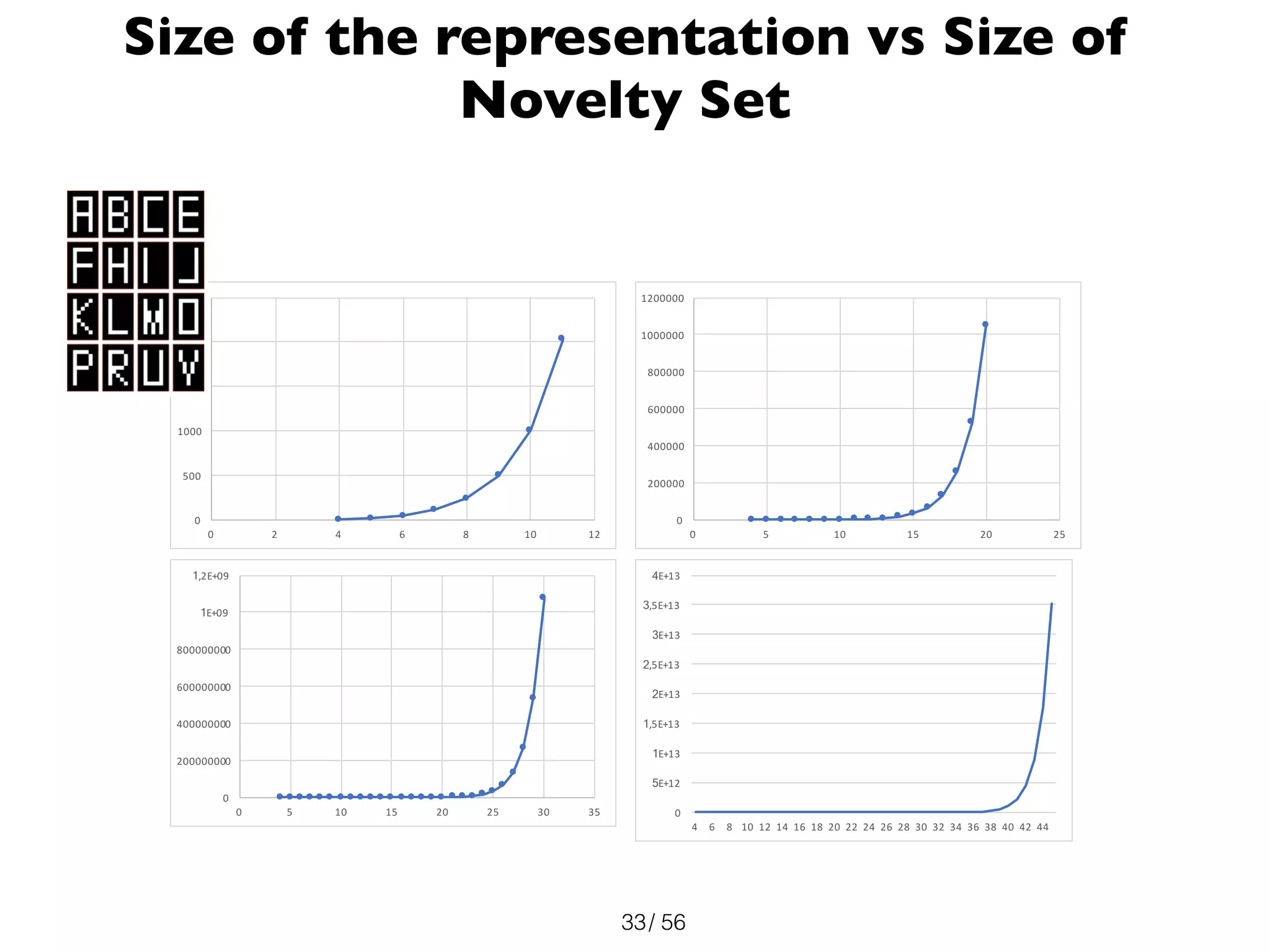
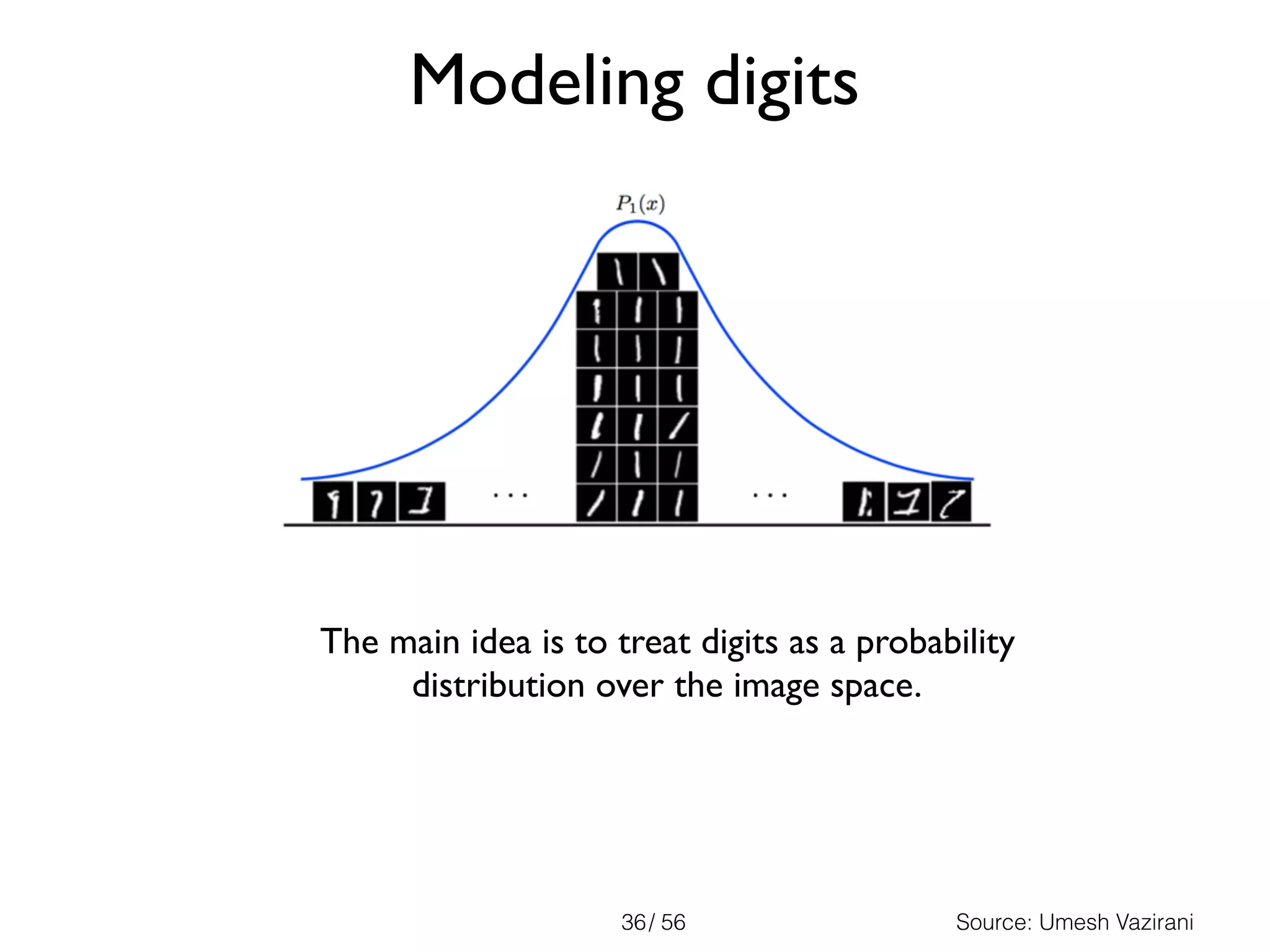
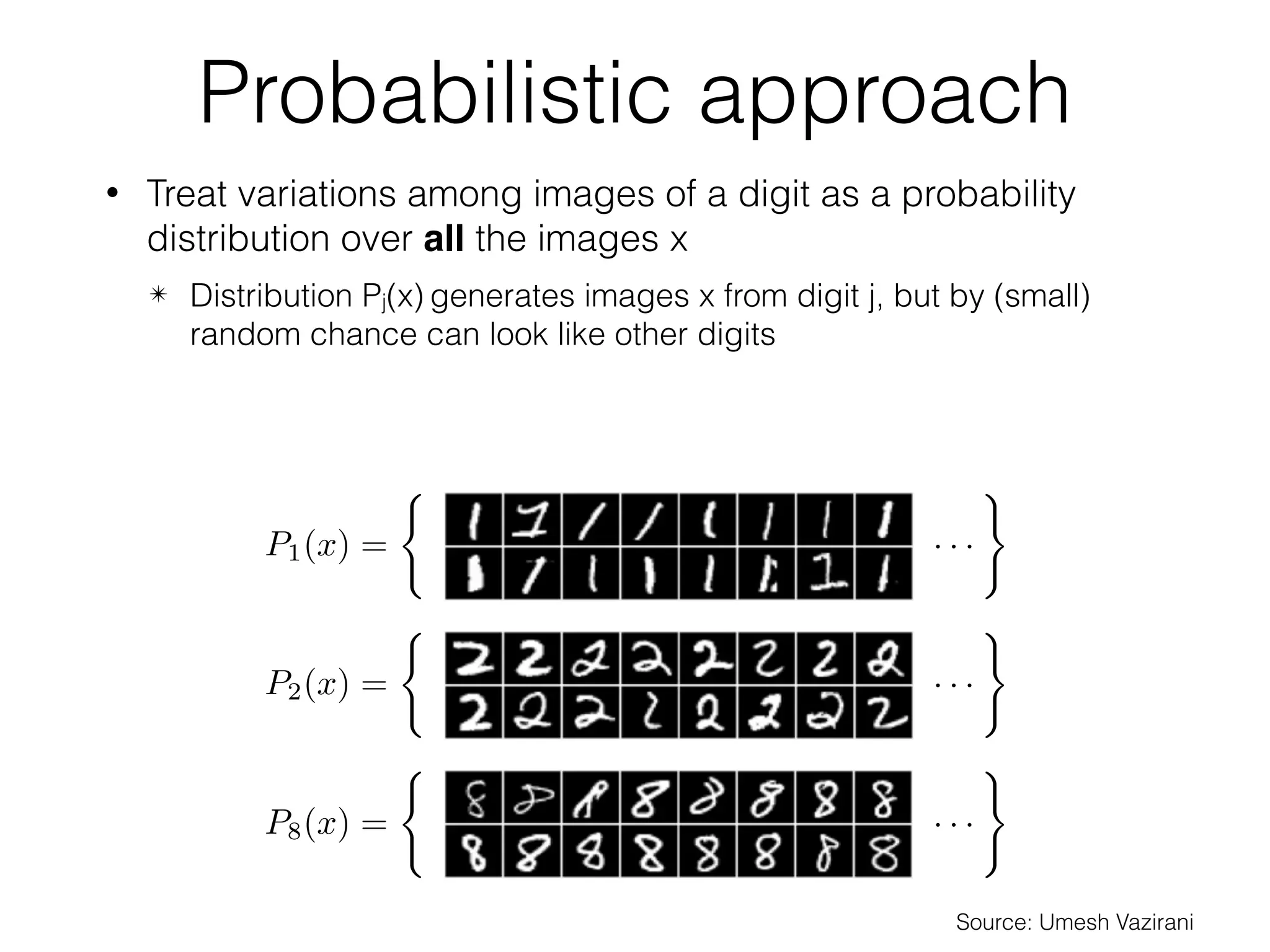
The document discusses the significance of representations in data science, specifically regarding learning and generating novelty through neural networks. It explores how various representations affect the modeling of objects, including handwritten digits, using techniques like Naive Bayes and deep neural networks. The emphasis is on understanding the generative potential of these models and the implications of representation on learning and novelty generation.

1. / 56
Generativity and Data Science
1
Akın Kazakçı (Mines Paristech)
akin.kazakci@mines-paristech.fr

2. 2
Prediction
A quest for artificial general intelligence

3. 3
Prediction Novelty generation
A quest for artificial general intelligence

4. / 56
Plan
• Representation and learning
• Impact of representations on generation
• A naive bayes generator
• Generating novelty with neural networks
4

5. / 56
How do you
represent this
“object”?
5
Representing an object
A

6. / 56
What is a
representation?
6
Representing an object
A

7. / 567
Representing an object
A
Source: https://plato.stanford.edu/entries/
mental-representation/
Have fun!
Very hard question.

8. / 568
Representing an object
A
Even the simplest of (computer) representations
require some choice or arbitrariness.
AObject (?) Pixel representation (8x9)

9. / 569
To process any “object” (e.g. by computers)
you need to “represent” it.

10. / 5610
Representation are not “neutral” and
“independent” of the observer.

11. / 56
What effect a representation have
on learning and (or) generation?

12. / 56
Let us take a toy
example; 16 letters
Each represented
with 9x5 binary
pixels
12
Representation and Learning

13. / 56
What is the size of
the representation
space?
13
Representation and Learning

14. / 56
There are 245 object
(representations) in
that space.
14
Representation and Learning

15. / 56
Each image can be
represented as a vector of
size 45.
15
Representation and Learning
(0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1, 0,0 …………………..…… 0,0,0,0,0)
(0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1, 0,1 …………………..…… 0,0,0,0,0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.

16. / 56
What can be learned
from this data?
16
Representation and Learning
(0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1, 0,0 …………………..…… 0,0,0,0,0)
(0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1, 0,1 …………………..…… 0,0,0,0,0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.

17. / 56
The first and the simplest thing
we can ‘consider’ learning is the
data itself (e.g. identity function).
17
Representation and Learning
(0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1, 0,0 …………………..…… 0,0,0,0,0)
(0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1, 0,1 …………………..…… 0,0,0,0,0)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
The identity function can be
conceived as a mapping from the
image to its vectorised
representation.
What would be the inconvenient of
such a function?

18. / 5618
Representation and Learning
A
The new ‘A’ will be
unrecognisable by Id(x)

19. / 5619
Learning assumes a notion of
‘generalisation’

20. / 5620
Representation and Learning
What generalisations can we
learn from these letters ?
Here is an example:

21. / 5621
Representation and Learning
Learning means finding
regularities or structures in
representations.
Where structure is the
dependence of pixels (e.g.
co-occurence)

22. / 5622
Re-representing objects
We can use the following
structures to re-represent letters.
For example,

23. / 56
Objects can be represented in
multiple ways
In design literature, it has been acknowledged that
objects can be represented in multiple ways
Images from Reich, A ciritcal review of general design theory, RED, 1995

24. / 5624
Re-representing objects

25. / 56
Strokes gives us a shorter
representation (or code) for the
letter domain.
25

26. / 56
This new representation is
lossless compression (no
information lost)
26

27. / 56
Each representation is a model
And the set of models of a given
agent is its knowledge.
27

28. / 56
Models can be imperfect
(e.g. lossy).
28

29. / 56
One example of imperfect
models are probabilistic models.
29

30. / 56
Plan
• Representation and learning
• Impact of representations on (probabilistic)
generation
• A naive bayes generator
• Generating novelty with neural networks
30

31. / 56
We generate pixels
randomly uniformly.
Everything seems new.
But it is hard to find any
structure in this data.
31
The impact of representations on novelty
generation

32. / 5632
Pixel space Stroke space
Representations change what you can
generate

33. / 56
Size of the representation vs Size of
Novelty Set
33
0
500
1000
1500
2000
2500
0 2 4 6 8 10 12
0
5E+12
1E+13
1,5E+13
2E+13
2,5E+13
3E+13
3,5E+13
4E+13
4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44
0
200000000
400000000
600000000
800000000
1E+09
1,2E+09
0 5 10 15 20 25 30 35
0
200000
400000
600000
800000
1000000
1200000
0 5 10 15 20 25

34. / 56
Plan
• Representation and learning
• Impact of representations on (probabilistic) generation
• A naive bayes generator
• Generating novelty with neural networks
34

35. / 5635
Assume we have 60K handwritten digits.
How to model them?

36. / 56
Modeling digits
36
The main idea is to treat digits as a probability
distribution over the image space.
Source: Umesh Vazirani

37. / 5637
Probabilistic approach
• Treat variations among images of a digit as a probability
distribution over all the images x
✴ Distribution Pj(x) generates images x from digit j, but by (small)
random chance can look like other digits
✴ Imperfect model, represents our uncertainty/ambiguity, but Bayes’
rule to the rescue!
P1(x) =
(
P2(x) =
(
P8(x) =
(
· · ·
)
· · ·
)
· · ·
)
Source: Umesh Vazirani

38. / 5638
Estimating the distributions
• Use training data to estimate the prior and the
class-conditional distributions
✴ MNIST dataset: 60K training data, 10K test data
• Estimating the is easy:
• From MNIST:
• But estimating the is difficult!
⇡j = Pr[y = j]
Pj(x) = P(x | y = j)
⇡j
Pj(x)
ˆ⇡j =
nj
n
=
# of examples of class j
total # of examples
j 0 1 2 3 4 5 6 7 8 9
ˆ⇡j (%) 9.87 11.24 9.93 10.22 9.74 9.03 9.86 10.44 9.75 9.92
Source: Umesh Vazirani
Naive Bayes
• Convert grayscale images to binary
• A general distribution over has parameters
threshold binary data
x 2 {0, 1}784
{0, 1}784
2784
1
• Assume that within each class, the individual pixel values
are independent:
• Each is a coin flip: easy to estimate!
• Now only have 784 parameters to learn
Pj(x) = Pj1(x1) · Pj2(x2) · · · Pj,784(x784)
Pji
Source: Umesh Vazirani

39. / 5639
Naive Bayes on MNIST
• Error rate: 15.4% (on 10K test data) —> pretty good!
• Mean vectors for each class (the ’s):pji
• Samples from the trained model:
Source: Umesh Vazirani

40. / 56
Plan
• Representation and learning
• Impact of representations on generation
• A naive bayes generator
• Generating novelty with neural networks
40

41. / 5641
Machine learning proposes powerful
generative models

42. / 5642
but these powerful models are used
to regenerate objects that we can
relate easily to known objects…

43. / 56
• Although trained for
generating what we know,
some models can generate
unrecognizable objects
• However, these models and
samples are considered as
spurious (Bengio et al. 2013),
or as a failure(Salimans et al.
2016)
43

44. / 56
So, first task is to demonstrate that
there is a lot more generative potential
in DNNs than what was intended
44

45. / 56
Deep Neural Networks
45
Learning a sequence of
transformations of the
original representation
Main advantages
• Compositionality
• Hierarchy

46. Auto-associative neural nets
a.k.a auto-encoders
Learning to
disassemble
Learning to
build
- Auto-encoders have existed for
long time (Kramer 1991)
- Deep variants are more recent
(Hinton, Salakhutdinov, 2006;
Bengio 2009)
- A deep auto-encoder learns
successive transformations that
decompose and then
recompose a set of training
objects
- The depth allows learning a
hierarchy of transformations

47. / 56
• We use an iterative method to generate new images
• Start with a random image
• Force the network to construct (i.e. interpret)
• , until convergence, f(x) = dec(enc(x))
47
The generative process

48. / 56
Generation to get back to knowledge
48

49. / 5649
A map of the known digit instances
Kazakçı, Cherti, Kégl, 2016

50. / 5650
A map of the known digit instances

51. / 5651
A map of the known digit instances
Kazakçı, Cherti, Kégl, 2016

52. / 5652
A map of the known digit instances
Kazakçı, Cherti, Kégl, 2016

53. / 5653Kazakçı, Cherti, Kégl, 2016
A map of the known digit instances

54. / 5654
Known Training digits
Representable “Combinations of strokes”
54
What is the target? - Value referentials
Our interpretation
of the results:

55. / 5655
Known Training digits
Representable All digits that the model can generate
Valuable All recognizable digits
What traditional ML wants

56. / 5656
Known Training digits
Representable “Combinations of strokes”
Valuable Human selection
What novelty generation aims at

57. Discussion