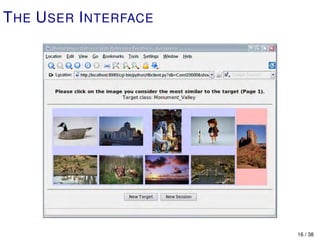
This document describes a statistical framework for interactive image category search based on mental matching. The framework allows a user to search an unstructured image database for a target category that exists only as a "mental picture" by providing feedback on displayed image sets. At each iteration, the system selects images to maximize the information gained from the user's response. The goal is to minimize the number of iterations needed to display an image from the target category. Experiments showed the approach was effective on databases containing tens of thousands of images across several semantic categories.

1. I NTERACTIVE S EARCH FOR
I MAGE C ATEGORIES BY
M ENTAL M ATCHING
Donald Geman
Johns Hopkins University
Frontiers in Computer Vision
M.I.T., August 2011

2. R EFERENCE
IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 31, NO. 6, JUNE 2009 1087
A Statistical Framework for
Image Category Search from a Mental Picture
Marin Ferecatu and Donald Geman, Senior Member, IEEE
Abstract—Starting from a member of an image database designated the “query image,” traditional image retrieval techniques, for
example, search by visual similarity, allow one to locate additional instances of a target category residing in the database. However, in
many cases, the query image or, more generally, the target category, resides only in the mind of the user as a set of subjective visual
patterns, psychological impressions, or “mental pictures.” Consequently, since image databases available today are often unstructured
and lack reliable semantic annotations, it is often not obvious how to initiate a search session; this is the “page zero problem.” We
propose a new statistical framework based on relevance feedback to locate an instance of a semantic category in an unstructured
image database with no semantic annotation. A search session is initiated from a random sample of images. At each retrieval round,
the user is asked to select one image from among a set of displayed images—the one that is closest in his opinion to the target class.
The matching is then “mental.” Performance is measured by the number of iterations necessary to display an image which satisfies the
user, at which point standard techniques can be employed to display other instances. Our core contribution is a Bayesian formulation
which scales to large databases. The two key components are a response model which accounts for the user’s subjective perception of
similarity and a display algorithm which seeks to maximize the flow of information. Experiments with real users and two databases of 2 / 38

3. S CENARIO
3 / 38

4. O UTLINE
Standard Image Retrieval
Mental Matching
Experiments
Statistical Framework (maybe)
Modeling Human Behavior (maybe)
4 / 38

5. C ONVENTIONAL Q UERY- BY-E XAMPLE (QBE)
Start from a query image in a database. Find other images
which are “close” or “closest”
in overall color, texture or shape, or
in a semantic sense, or . . .
Matching is performed by the system.
Good results in limited domains, e.g., comparing paintings,
plants and landscapes.
5 / 38

6. E XAMPLE : IKONA S EARCH E NGINE (INRIA)
6 / 38

7. E XAMPLE ( CONT )
7 / 38

8. “PAGE Z ERO ” P ROBLEM
QBE requires a starting point - a query image.
Dilemma: Without a starting point, random sampling a large
database is too slow in practice.
8 / 38

9. E XTERNAL I MAGES
Mental Picture: The user has a picture “in mind”, e.g., a
face or painting or house.
Viewed Image: The user is looking at a picture, e.g., in a
magazine or on the web.
Physical Object: The user is holding an object.
9 / 38

10. W HO IS THAT P ERSON ?
10 / 38

11. M ENTAL C ATEGORY S EARCH
Assume this “external query” is represented in our
database, either by
a version of the same image (e.g., same person), or
variations on a theme, i.e., a category of images (e.g.,
similar houses).
Objective: Find an efficient way to display this version or
representatives of this category.
Applications: Image retrieval (“page zero”); web browsing;
security; art management; plant science; e-commerces;
blah blah blah.
11 / 38

12. I NTERACTIVE S EARCH
The object of the search is a class S (variations on an
image or theme).
Single target search is the special |S| = 1.
Assume the user always recognizes an instance of his
target.
At each iteration, some images are displayed, typically two
to sixteen.
The user responds by either
signaling a target if present; or
choosing the one deemed “closest”.
12 / 38

13. I NTERACTIVE S EARCH ( CONT )
Based on this feedback, the system chooses another set of
images to display.
Goal: Minimize the number of iterations until an exemplar of
the target is displayed.
Then display other examples (“page zero”) for specialization
and refinement.
13 / 38

14. B ACK TO K ERMIT
14 / 38

15. C OMPLICATIONS
Mental matching involves human memory, perception and
opinions.
People are semantically oriented. However, images are
indexed by low-level features (“semantic gap”).
Interest in large databases, order 10,000 to 1,000,000.
15 / 38

16. T HE U SER I NTERFACE
16 / 38

17. M EASURES OF P ERFORMANCE
T : number of iterations until S is displayed.
P(T < t): The probability distribution over some population
of users.
E(T ): The mean of this population.
For a random search,
E(T ) ∼ N/(L(|S| + 1)),
=
where N is the size of the database and L is the number
displayed per iteration.
Coherence: The probability that the user selects the i’th
closest image to S.
17 / 38

18. E XPERIMENTAL DATABASES
Corel: N=60,000 images
Alinari: N=20,000 images
Ground truth: 10 semantic classes of ≈ 100 hand-chosen
images
18 / 38

19. A LINARI DATABASE
19 / 38

20. P ERFORMANCE : A LINARI
Search time distribution
20 / 38

21. C ONCLUSIONS
Rich possibilities for mathematical modeling in building
efficient man-machine interfaces.
Mixes geometry, probability, optimization and information
theory.
Solving the “vision problem” is probably not around the
corner.
Hence extending to databases of order 1,000,000 remains
a challenge.
21 / 38

22. DATABASE AND I MAGE M ETRIC
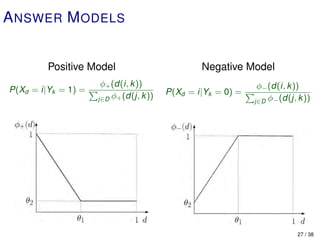
I . . . an image
Ω = {1, 2, ..., N} . . . a database of images
We do not assume Ω is “structured” (partitioned into
categories)
{f (I1 ), f (I2 ), . . . , f (IN )} . . . “features” in R M .
df : R M × R M → [0, 1] . . . a metric on features.
S ⊂ Ω . . . the category (semantic class) in the mind of the
user, a random set.
For each k = 1, ..., N, define a binary random variable
Yk = 1 if k ∈ S
Yk = 0 if k ∈ S
22 / 38

23. D ISPLAY
D ⊂ {1, 2, . . . , N} . . . a set of L distinct images.
Dt . . . the images displayed at time t = 1, 2, . . .
XD . . . the response of the user to D.
For D ∩ S = ∅, XD = i means i is “closest” to S,
in the opinion of the user
23 / 38

24. S EARCH H ISTORY
History (“evidence”) after t steps:
Bt = {D1 = d1 , XD1 = i1 , . . . , Dt = dt , XDt = it }
= {D1 = d1 , XD1 = i1 , XD2 = i2 , . . . , Dt = dt , XDt = it }
because D1 is chosen at random and Ds+1 will depend only
on D1 and the previous answers (actually on the posterior).
Given S and Dt , the answer XDt is independent of the
search history:
P(XDt = i|S, Bt ) = P(Xd = i|S, Dt = d)
24 / 38

25. D ISPLAY C RITERION
Dt+1 = arg max I(XD ; S|Bt )
D
25 / 38

26. S EPARATE B AYESIAN S YSTEMS FOR E ACH
k ∈Ω
Prior model:
p0 (k) = P(Yk = 1) = P(k ∈ S)
Answer model: For k ∈ D, i ∈ D,
q+ (i|k, D) = P(XD = i|Yk = 1)
q− (i|k, D) = P(XD = i|Yk = 0)
Posterior distribution at step t:
pt (k) = P(Yk = 1|Bt )
26 / 38

27. A NSWER M ODELS
Positive Model Negative Model
φ+ (d(i, k )) φ− (d(i, k ))
P(Xd = i|Yk = 1) = P(Xd = i|Yk = 0) =
j∈D φ+ (d(j, k )) j∈D φ− (d(j, k ))
27 / 38

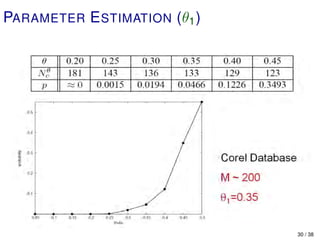
28. PARAMETER E STIMATION (θ1 )
The positive model
Θ1 : “no preference” threshold
Repeat M times:
1. Fix θ and k ∈ S.
2. Choose two images i, j such that:
(a) d(i, k ) ≈ θ
(b) d(j, k ) is chosen uniformly in [θ, 1]
3. Display i, j and record the user’s
choice.
28 / 38

29. PARAMETER E STIMATION (θ1 )
Consider two hypotheses:
H0: “no preference”
H1: “preference for i (closest)”
Let N θ be the number of times the user chooses i. Under H0,
1
N θ ∼ Bin(M, )
2
Let p(θ) = P(Bin(M, 1 ) > N θ ).
2
Choose the largest value of θ such that H0 is rejected at
p = 0.05.
29 / 38

30. PARAMETER E STIMATION (θ1 )
30 / 38

31. PARAMETER E STIMATION (θ2 )
The positive model
Θ2 : degree of coherence with system metric
Repeat M times:
1. Fix θ and k ∈ S.
2. Choose a display D such that:
(a) One image i in D is very close to some k ∈ S;
(b) All the other images in D are more than θ1 units away from k.
3. Display D and record the user’s choice.
31 / 38

32. PARAMETER E STIMATION (θ2 )
1
P(XD = xi |Yk = 1) ∼
=
1 + (n − 1)θ2
1 P(XD = xi |Yk = 1)
θ2 ∼
+
=
n − 1 P(XD = xi |Yk = 1)
Corel database (M=600):
θ2 = 0.065
32 / 38

33. U PDATE M ODEL
The new posterior distribution is
pt+1 (k) = P(Yk = 1|Bt+1 )
which reduces to
P(XDt+1 = i|Yk = 1, Dt+1 )pt (k)
P(XDt+1 = i|Yk = 1, Dt+1 )pt (k) + P(XDt+1 = i|Yk = 0, Dt+1 )(1 − pt (k )
which is finally
q+ (i|k, Dt+1 )pt (k )
.
q+ (i|k, Dt+1 )pt (k) + q− (i|k, Dt+1 )(1 − pt (k))
33 / 38

34. TAKING S TOCK
So mental category search reduces to two difficult tasks:
An optimization problem: Discover approximations to the
optimal display.
A modeling problem: Discover answer models which match
human behavior.
34 / 38

35. I DEAL U SER
Suppose d(i, S) < d(j, S) for each j ∈ D, i ∈ D. Ideal user:
P(XD = i|S) = 1
Since S determines XD :
.
Dt+1 = arg max I(XD ; S|Bt )
D
= arg max(H(XD |Bt ) − H(XD |S, Bt ))
D
= arg max H(XD |Bt ),
D
which motivates the following choice of display:
35 / 38

36. O PTIMAL D ISPLAY: T HE VORONOI C ELLS
H AVE E QUAL M ASS
36 / 38