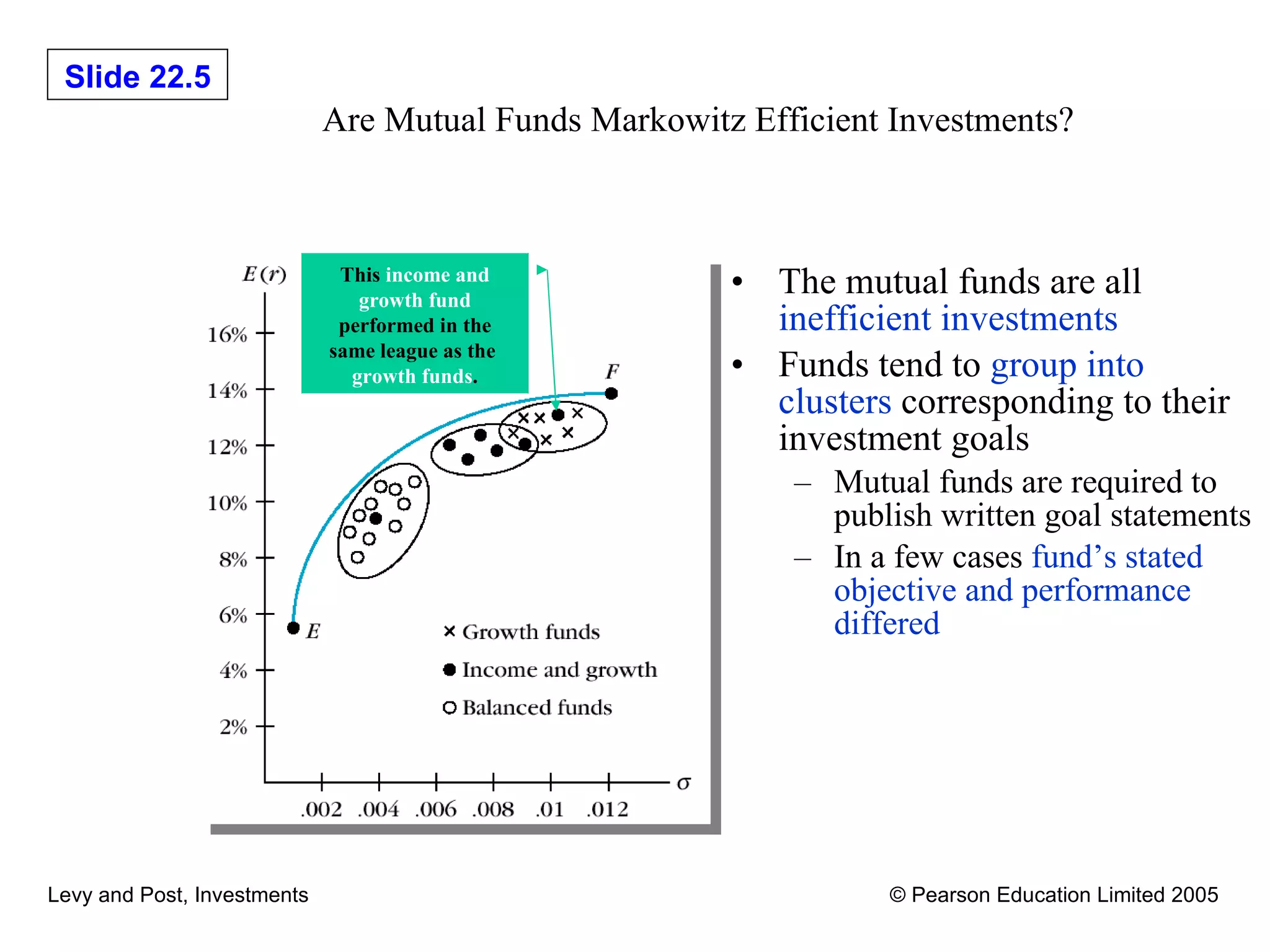
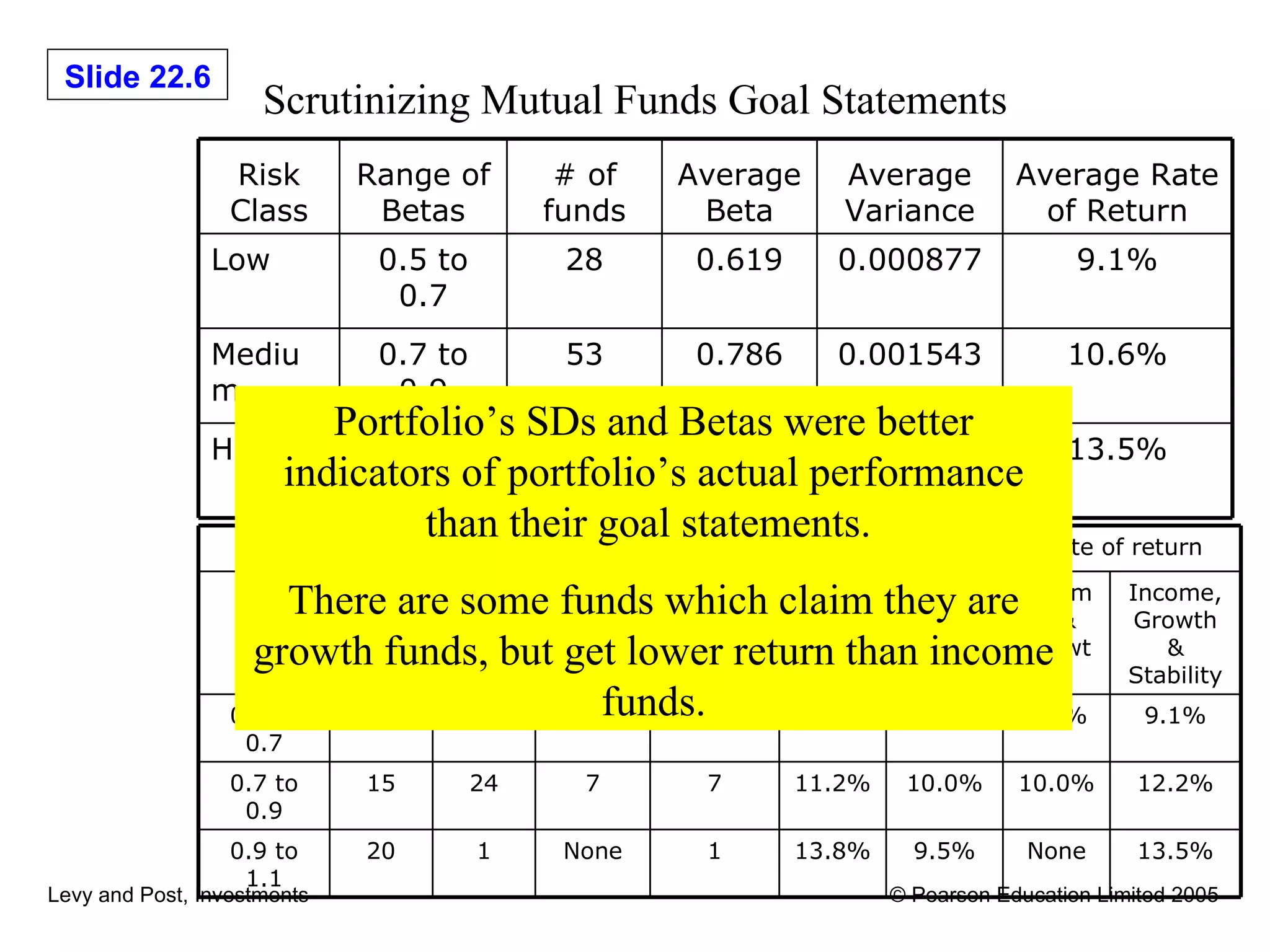
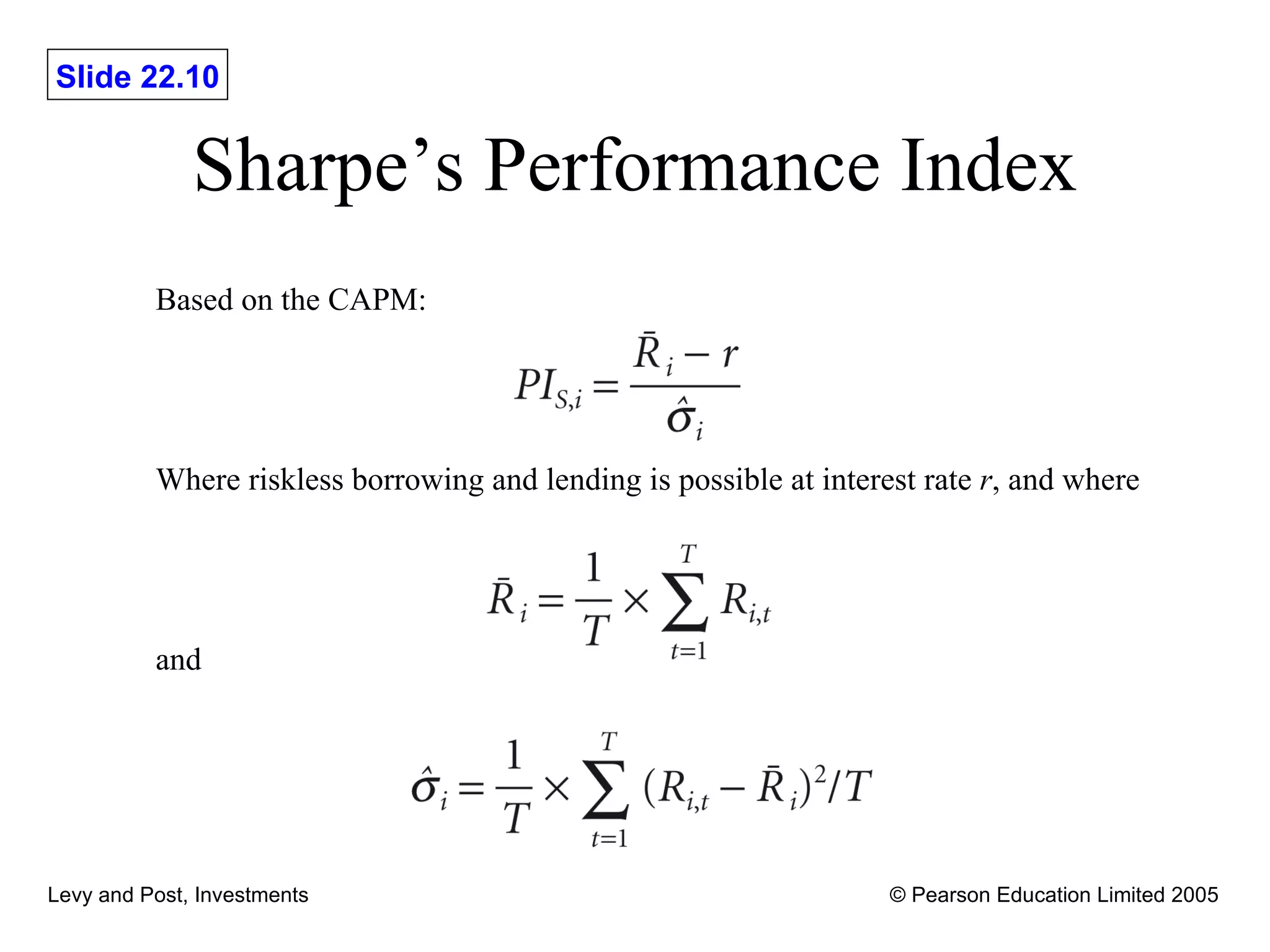
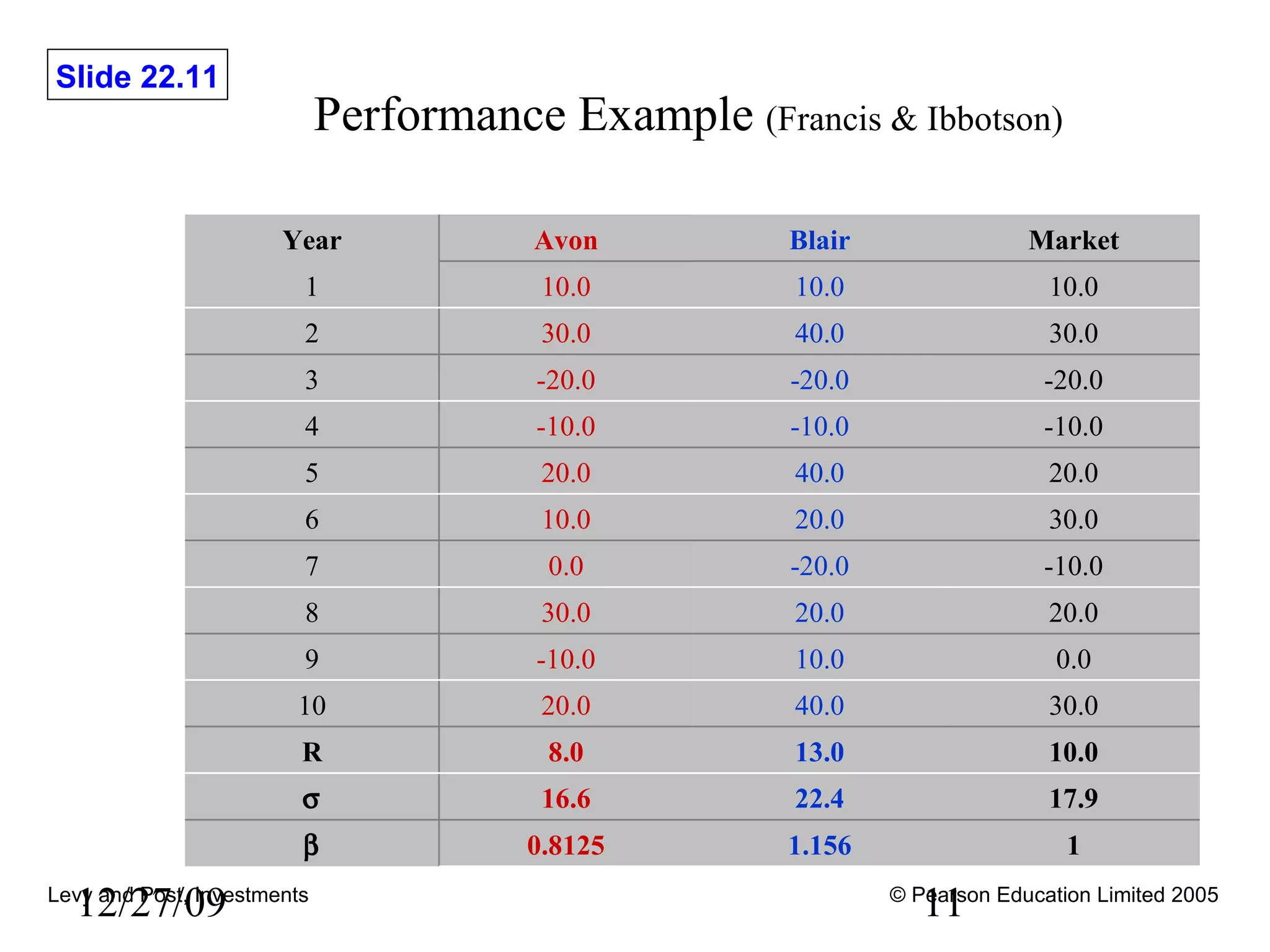
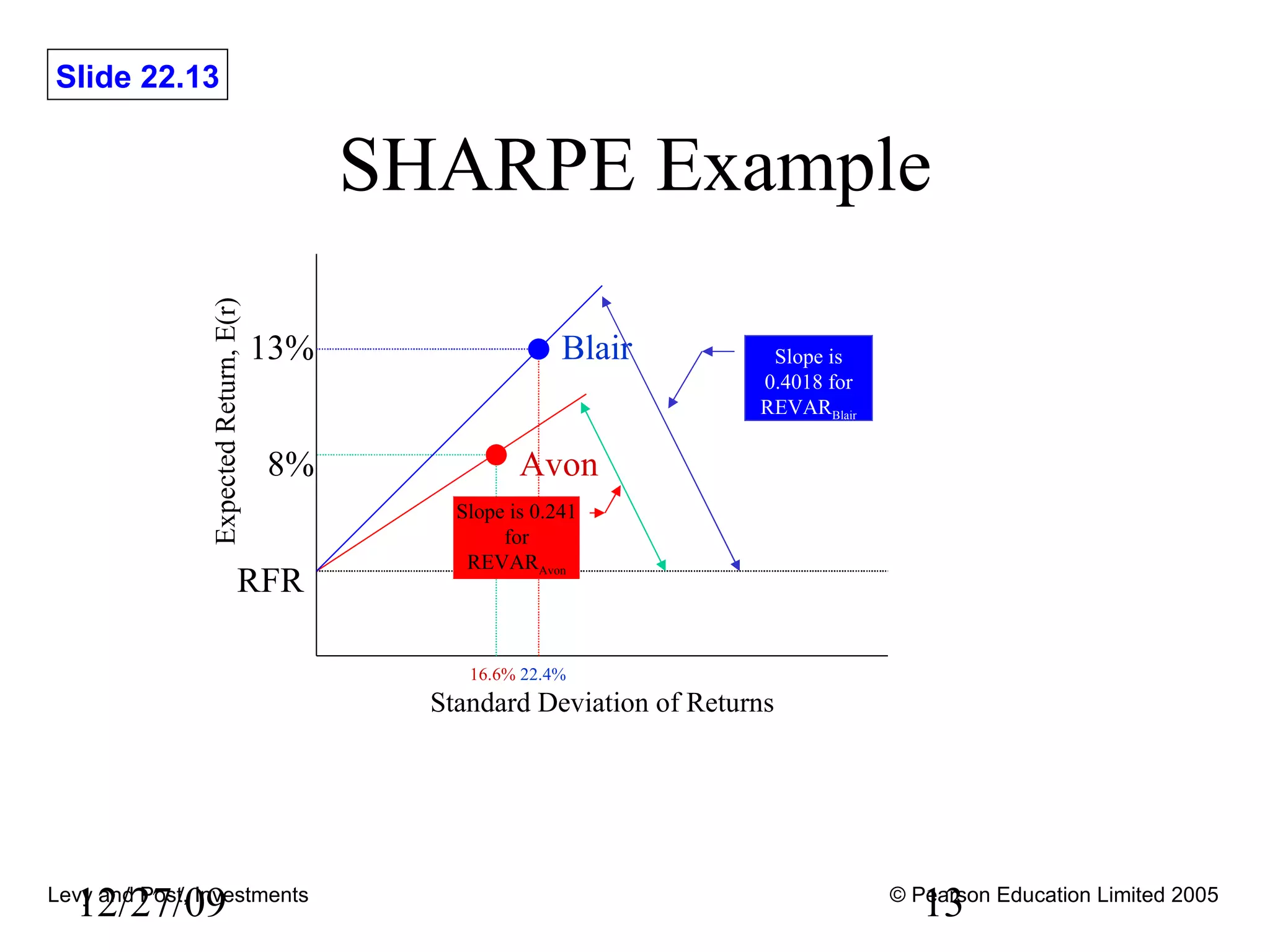
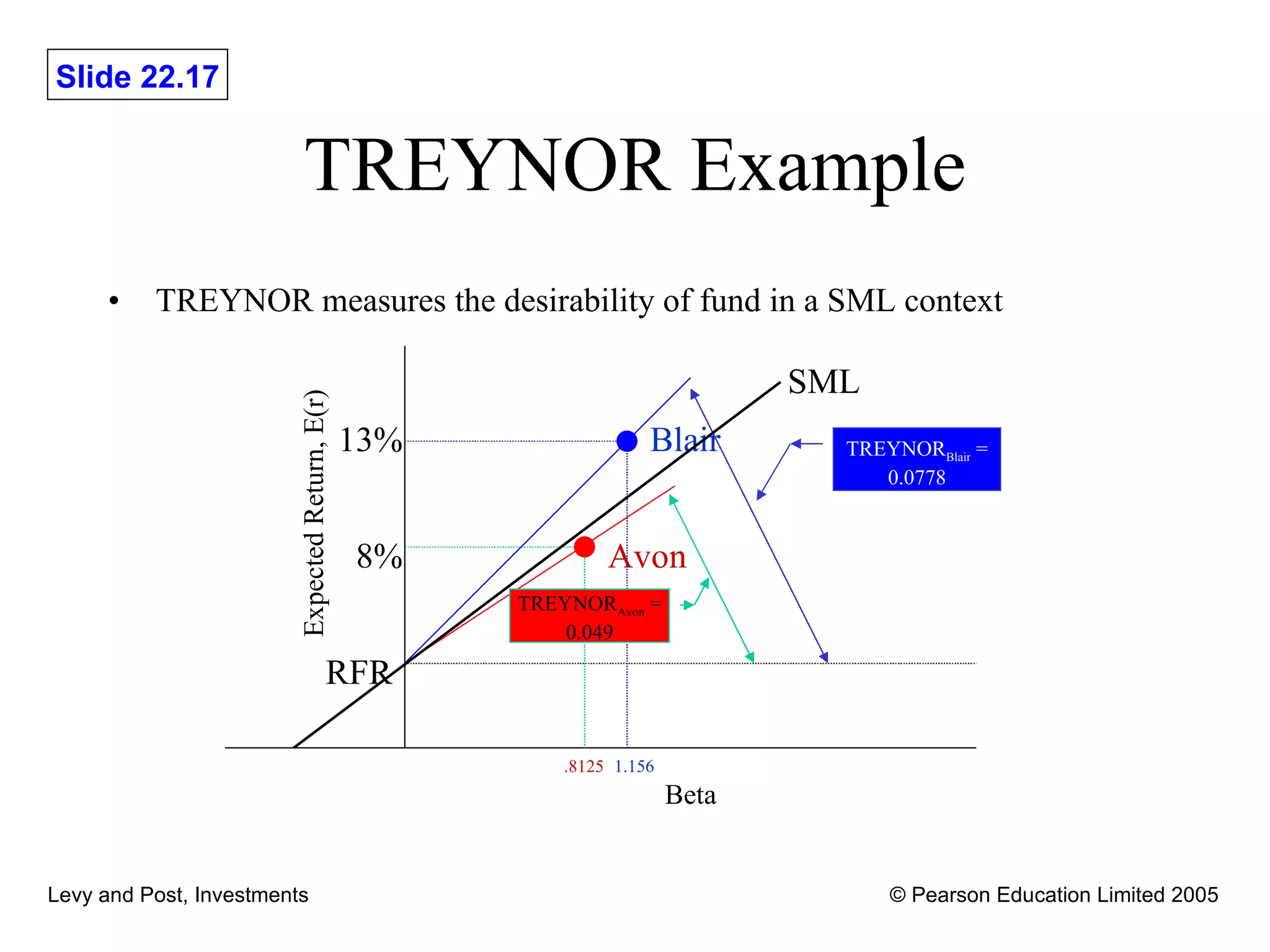
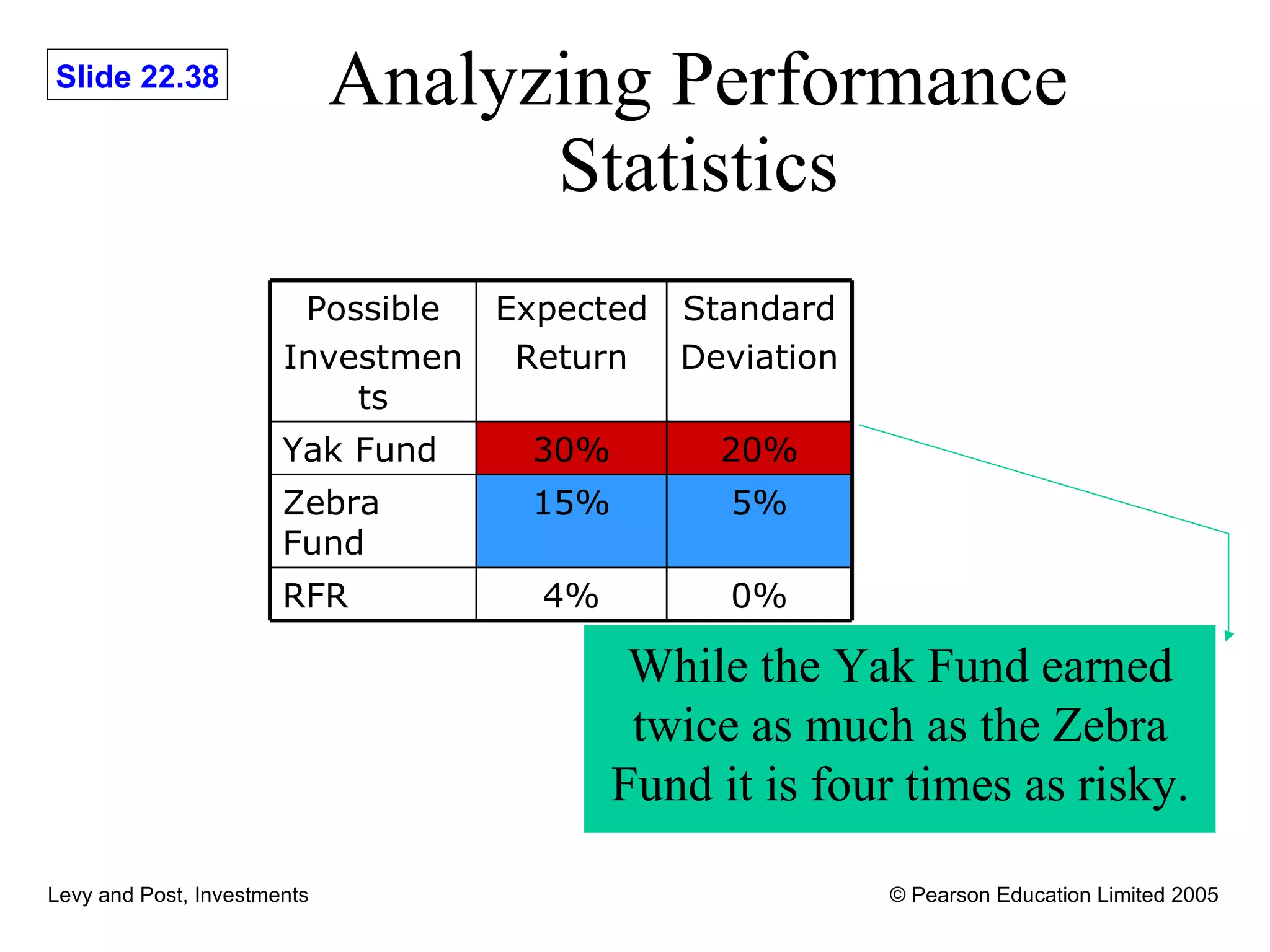
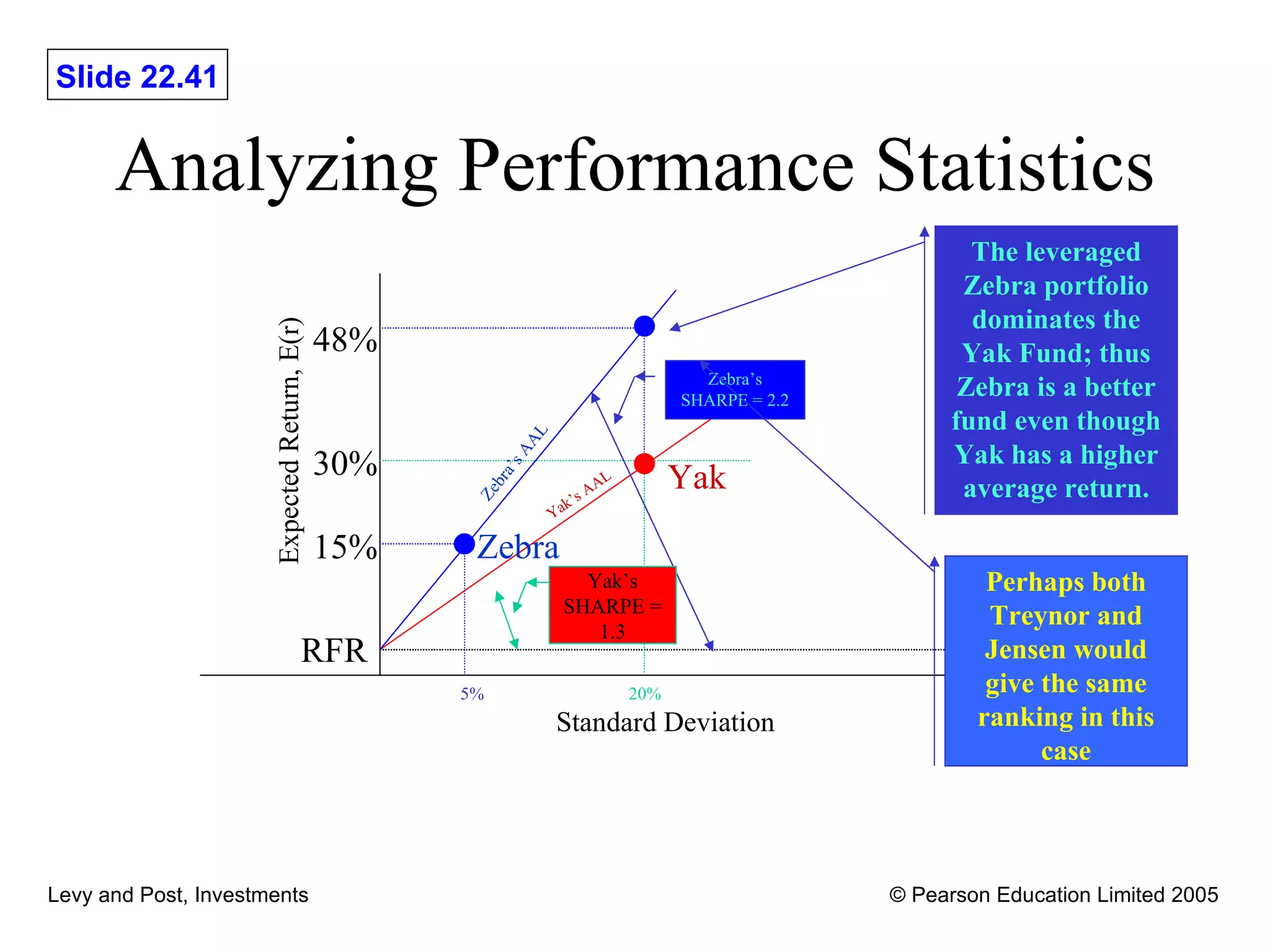
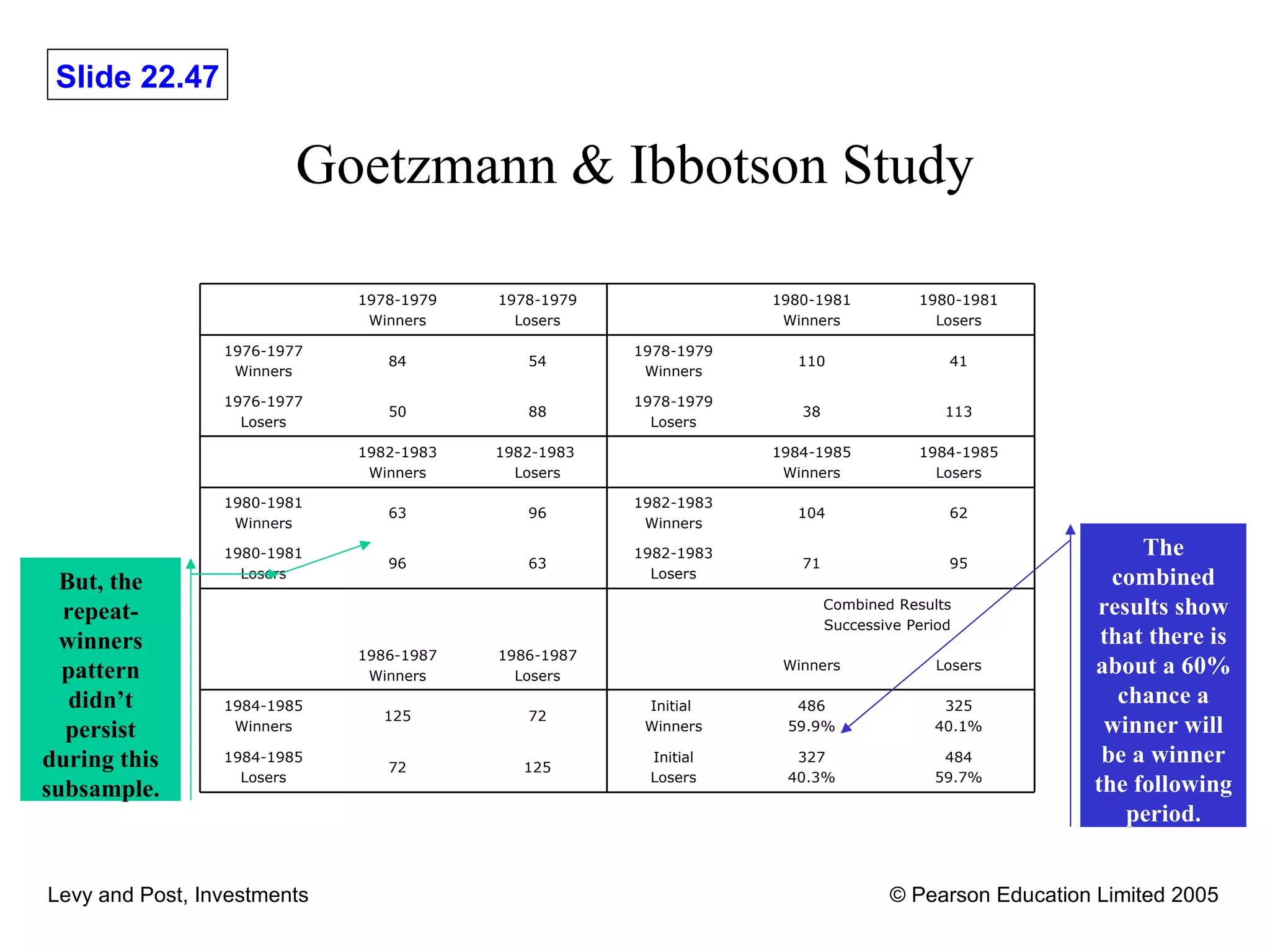
This document discusses various methods for evaluating investment performance, including risk-adjusted performance indexes. It describes tools like Sharpe's performance index, Treynor's performance index, and Jensen's performance index that measure performance based on risk and return. It also cautions that performance evaluation is historical and notes difficulties in accurately measuring risk and performance.

1. Investments Chapter 22: Performance Evaluation

2. General Tools for Performance Evaluation Compare performance with risk-adjusted performance indexes. Compare performance against benchmark portfolios. Use of performance attribution methods. Use of comparison universe methods.

3. How Should Investors Measure Risk? Standard Deviation (absolute risk) Investors with limited holdings Beta (relative risk) Investors with a wide array of holding 12/27/09

4. Words of Caution when using Performance Evaluation Performance evaluation is an historical exercise while most investors are interested in the future performance of portfolios. Correcting the performance for risk is very difficult. It is very difficult to obtain reliable estimates of the risk and return characteristics of individual securities. The portfolio compositions change over time.

5. Are Mutual Funds Markowitz Efficient Investments? The mutual funds are all inefficient investments Funds tend to group into clusters corresponding to their investment goals Mutual funds are required to publish written goal statements In a few cases fund’s stated objective and performance differed This income and growth fund performed in the same league as the growth funds .

6. Scrutinizing Mutual Funds Goal Statements Portfolio’s SDs and Betas were better indicators of portfolio’s actual performance than their goal statements. There are some funds which claim they are growth funds, but get lower return than income funds. # of funds claiming each goal Category’s average rate of return Beta Growth Growth & income Income & Growth Income, Growth & Stability Growth Growth & income Income & Growth Income, Growth & Stability 0.5 to 0.7 3 5 4 16 6.9% 10.1% 9.7% 9.1% 0.7 to 0.9 15 24 7 7 11.2% 10.0% 10.0% 12.2% 0.9 to 1.1 20 1 None 1 13.8% 9.5% None 13.5% Risk Class Range of Betas # of funds Average Beta Average Variance Average Rate of Return Low 0.5 to 0.7 28 0.619 0.000877 9.1% Medium 0.7 to 0.9 53 0.786 0.001543 10.6% High 0.9 to 1.1 22 0.992 0.002304 13.5%

7. Mutual Fund Performance The empirical evidence finds consistently that mutual fund managers on average lag behind the market if one corrects for risk and costs. Also, there seems to be little consistency in the performance of mutual funds over time.

8. Risk-adjusted Performance Measures Sharpe’s Performance Index. Treynor’s Performance Index. Jensen’s Performance Index. APT-based performance measures.

9. Sharpe’s Performance Index Based on the Slope of the CML Uses Standard Deviation to Measure Risk (i.e. the interest is to minimize total risk) The Higher the Index, the better the performance Investors Hold Only the Mutual Fund May wish to rank portfolios’ performances Need a measure that includes both risk and return Sharpe measured the reward to variability index

10. Sharpe’s Performance Index Based on the CAPM: Where riskless borrowing and lending is possible at interest rate r , and where and

11. Performance Example (Francis & Ibbotson) 12/27/09 Year Avon Blair Market 1 10.0 10.0 10.0 2 30.0 40.0 30.0 3 -20.0 -20.0 -20.0 4 -10.0 -10.0 -10.0 5 20.0 40.0 20.0 6 10.0 20.0 30.0 7 0.0 -20.0 -10.0 8 30.0 20.0 20.0 9 -10.0 10.0 0.0 10 20.0 40.0 30.0 R 8.0 13.0 10.0  16.6 22.4 17.9  0.8125 1.156 1

12. SHARPE Example The Avon Fund earned an average return of 8% annually with a standard deviation of 16.6%, while the Blair Fund earned 13.00% annually with a standard deviation of 22.4%. During the same time period the average risk-free rate was 4%. Which fund was the better performer? Since SHARPE Blair > SHARPE Avon , Blair was the better performer on a risk-adjusted basis.

13. SHARPE Example 12/27/09 Avon RFR 13% 8% 22.4% 16.6% Standard Deviation of Returns Expected Return, E(r) Blair Slope is 0.4018 for REVAR Blair Slope is 0.241 for REVAR Avon

14. Treynor’s Performance Index Based on SML Uses Beta to measure Risk (i.e. the interest is to minimize the market risk) The Higher the Index, the better the performance Investors Hold Many Assets For Investors Only Interested in Whether They Beat the Market Treynor devised measure to evaluate performance that uses systematic risk (beta) rather than total risk (standard deviation)

15. Treynor’s Performance Index Based on the APT: Where riskless borrowing and lending is possible at interest rate r , and where and

16. TREYNOR Example The Avon Fund earned an average return of 8% annually (Characteristic Line AVON : Intercept : -0.00125; Beta : 0.8125), while the Blair Fund earned 13.00% annually (Characteristic Line BLAIR : Intercept : 0.014; Beta : 1.156). During the same time period the average risk-free rate was 4%. Which fund was the better performer? Since TREYNOR Blair > TREYNOR Avon , Blair was the better performer on a risk-adjusted basis.

17. TREYNOR Example TREYNOR measures the desirability of fund in a SML context Avon RFR 13% 8% 1.156 .8125 Beta Expected Return, E(r) Blair TREYNOR Blair = 0.0778 TREYNOR Avon = 0.049 SML

18. TREYNOR Example Notice that the SML gives slightly different return for both funds! None of them is on the SML! The Avon Fund earned an average return of 8% annually because the Characteristic Line AVON : -0.00125 + 0.8125*(10% ) +  , where 10% = R m . According to the SML, the return to Avon Fund is: 4% + 0.8125*(10% - 4%) = 8.875% Similar differences are for the Blair Fund

19. Jensen’s Alpha Performance Index Based on CAPM Uses Beta to Measure Risk (equal to the vertical distance to SML) Determines How Much One Fund Outperforms or Underperforms Another Fund (neither Sharpe nor Treynor indicate by how much a fund has outperformed or underperformed the index) Determines the Significance of Results Investors Hold Many Assets

20. An Investment’s Alpha Jensen modified the characteristic line equation Rather than using periodic rates of return , he uses periodic risk-premiums With expected values (1) gets:

21. Explanation of an Investment’s Alpha Jensen’s alpha represents excess returns from asset Can be +, 0 or – If asset is correctly priced, Jensen’s alpha = 0 If alpha > 0 , asset has earned return greater than appropriate for its level of undiversifiable risk (beta) Asset is underpriced If alpha < 0 , asset’s returns are lower than appropriate for its level of risk Asset is overpriced

22. Jensen’s Alpha Example Using data ( risk premiums, not returns ) from Table 16-3 (previous slide) for the Avon and Blair Funds: Characteristic Line Avon Jensen’s alpha: -0.00875 Beta: 0.8125 Characteristic Line Blair Jensen’s alpha: +0.02062 Beta: 1.1562 Blair earned positive excess returns.

23. Jensen’s Alpha Example Econometric estimates of (1) Assume actual observations on all funds, market portfolio and risk free returns give the following alpha and beta values: In that case u = 0.03. This is the unik = specific risk of Avon fund

24. Caveats About Alphas Jensen’s alpha cannot be used to rank performance of different assets unless it’s adjusted for the assets’ risks ( same alphas does not imply same performance, because the vertical distance to the SML might be the same, but one fund might have much higher risk ) The appraisal ratio divides Jensen’s alpha by the standard error of the estimate (SE (u) ) which then allows for rankings Notice that the alpha = intercept of the original characteristic line (used to estimate our beta) is not the same as Jensen’s alpha and should not be used for investment performance evaluation

25. Caveats About Ranking Sharpe, Jensen & Treynor rank funds performances differently! If there are two funds (A, B) and the market index (M), and Treynor ranks for instance, A > M > B, so does Jensen. If there are many funds and the market index (M), Treynor may rank A > B first, while Jensen may rank K > L first.

26. Performance Indexes With APT One or More Factors Determine Risk Jensen’s Performance Measure Examine the Difference Between Actual and expected average rate of return Determines the Significance of Results For Investors Who Want to Compare Their Performance With Other Fund Managers

27. Empirical Evidence For MFs MFs performance Fall Behind the Market MFs can not Outperform the simple strategy: Buy-the-market and-hold policy International MFs Tend to do Better and: Outperform the S&P 500 Choice of market portfolio critical Bond Funds Underperform the Indexes Relationship underperformance and the expense ratio

28. Caution About Performance Indexes Problems Historical performance is used to infer future performance Difficult to measure the risk of activity traded accounts Beta is not stable Depends on the choice of market index Overall performance indexes cannot identify What activities of the portfolio manager resulted in the performance

29. Style Analysis: I An umbrella term for a set of tools for determining the investment style of portfolios and for measuring the performance of portfolios given their investment style. Money managers are evaluated, in part, based on how well they have offered what they promised or were told to do.

30. Style Analysis: II Holdings-based Style Analysis Determines the investment style of a portfolio by examining the characteristics of the individual securities in the portfolio. Returns-based Style Analysis Determines the investment style of a portfolio by analyzing its co-movements with indexes that proxy for different styles.

31. Selection of Money Manager These institutions/individuals must select a money manager This part presents tools for measuring and ranking money managers’ performances Aids in the selection process Money managers also use these tools to appraise and improve their skills

32. Analyzing a Portfolio Manager’s Style In 1992 Sharpe introduced a model to analyze a portfolio manager’s style ( i.e ., growth vs value investing, etc .) Uses modest amount of public information about funds Uses price indexes for 12 asset classes as explanatory variables for a mutual fund’s return Sample explanatory factors such as Soloman Brothers 90-day Treasury bill index Lehman Brothers Intermediate-Term Government Bond Index Sharpe/BARRA Value Stock Index

33. Analyzing a Portfolio Manager’s Style Uses factor analysis The factor loadings are estimates of the weights that a fund invests in the twelve asset categories R 2 of 0.70 are common Sharpe also suggests that same type of analysis could be done using a ‘rolling’ regression Repeating regression when new data is released—dropping oldest data and adding newest data 12/27/09

34. Performance Attribution The assessment of the performance of portfolio management decisions. Exhibit 22.7 Flow chart of the top-down money-management process Source: From Introduction to Investments, 2nd edn, by Levy. © 1999. Reprinted with permission of South-Western, a division of Thomson Learning: www.thomsonrights.com. Fax 800 730-2215.

35. Rolling Style Analysis Ibbotson Associates uses a rolling regression period of 60 months Deleting oldest month and adding new month as data becomes available Some fixed-income securities entered this growth stock fund in mid 1990s—this is interesting because Magellan’s published investment objective is a growth stock fund.

36. Benefits From Using Quantitative Management Style Analysis Quantitative style analysis is important due to: Investment holdings are usually not reported publicly until months after they are made—too late for investors to react in a timely manner Mutual funds can report misleading investment goals Can also provide better forecasts of mutual fund’s risk/return than subjective comments in newspapers, etc .

37. Analyzing Performance Statistics Mutual funds with the highest average rate of return might not have the highest rank because A highly aggressive fund may earn higher returns than a less aggressive fund but the higher returns may not be sufficient to compensate for the extra risk taken

38. Analyzing Performance Statistics While the Yak Fund earned twice as much as the Zebra Fund it is four times as risky. Possible Investments Expected Return Standard Deviation Yak Fund 30% 20% Zebra Fund 15% 5% RFR 4% 0%

39. Analyzing Performance Statistics By multiplying Zebra’s low SD by 4, we could create a new portfolio on Zebra’s Asset Allocation Line (AAL) with the same high SD as Yak Fund Borrow 4 times as much as the initial equity, invest in Zebra, and achieve the following E(R Zebra ): (4*0.15 - 4*0.04)= 0.48

40. Analyzing Performance Statistics Check that the SD is the same as for Yak Fund (see notes in SML, the risk free interest rate has zero variance)

41. Analyzing Performance Statistics The leveraged Zebra portfolio dominates the Yak Fund; thus Zebra is a better fund even though Yak has a higher average return. Perhaps both Treynor and Jensen would give the same ranking in this case Yak RFR 48% 30% 20% 5% Standard Deviation Expected Return, E(r) Zebra Zebra’s SHARPE = 2.2 Yak’s SHARPE = 1.3 15% Yak’s AAL Zebra’s AAL

42. General Discussion of Performance Measurement Tools When investors analyze merits of alternative investments, usually concerned with Asset selection Portfolio manager’s ability to select good investments and to not select poor investments Sharpe, Treynor & Jensen’s Alpha are good tools to evaluate this issue Market timing Portfolio manager’s ability to buy low/sell high and manager’s ability to react to changes in market’s direction Sharpe, Treynor & Jensen’s Alpha are not good tools for evaluating market timing unless theoretical framework is extended

43. Evaluating Timing Decisions Treynor & Mazuy included a second-order term in the characteristic line to evaluate market-timing

44. Evaluating Timing Decisions A successful market timer will Shift into high beta securities when bull market begins Shift into low beta securities when bear market begins If portfolio manager does this, beta 2,investment > 0 If portfolio manager cannot outguess market turns, beta 2,investment = 0 (statistically) If portfolio manager incorrectly predicts market turns, beta 2,investment < 0 12/27/09

45. Do Winners Repeat? Are the best portfolio managers able to repeat their high performance? If security markets are perfectly efficient, there should be no consistency in high performance When evaluating whether winners repeat, must be careful to not flaw study in terms of survivorship bias Market indexes only contain securities that have ‘survived’—not experienced bankruptcy, merger, etc . Goetzmann & Ibbotson studied mutual funds Mitigated survivorship bias by comparing funds within-sample performances through time

46. Goetzmann & Ibbotson Study Database Monthly total returns of several hundred mutual funds over a 13-year period Management fees deducted, but load, exit fees and taxes were not considered All cash flows reinvested monthly Returns measured over 2-year within-sample period, beginning in 1976 to predict out-of-sample performance for subsequent 2-year period Only funds in existence for entire 2-year interval included Every mutual fund categorized as ‘winner’ or ‘loser’ based on whether it ranked above or below that 2-year sample’s median return

47. Goetzmann & Ibbotson Study The combined results show that there is about a 60% chance a winner will be a winner the following period. But, the repeat-winners pattern didn’t persist during this subsample. 1978-1979 Winners 1978-1979 Losers 1980-1981 Winners 1980-1981 Losers 1976-1977 Winners 84 54 1978-1979 Winners 110 41 1976-1977 Losers 50 88 1978-1979 Losers 38 113 1982-1983 Winners 1982-1983 Losers 1984-1985 Winners 1984-1985 Losers 1980-1981 Winners 63 96 1982-1983 Winners 104 62 1980-1981 Losers 96 63 1982-1983 Losers 71 95 Combined Results Successive Period 1986-1987 Winners 1986-1987 Losers Winners Losers 1984-1985 Winners 125 72 Initial Winners 486 59.9% 325 40.1% 1984-1985 Losers 72 125 Initial Losers 327 40.3% 484 59.7%

48. Goetzmann & Ibbotson Study However, these high-return mutual funds could continue to have high-ranking returns due to high risk, not because they were winners G&I replicate study using risk-adjusted returns Computed Jensen’s Alpha for each fund Classified fund as a winner or loser if fund’s alpha > or < period’s median alpha Results show that winners tend to repeat in all 5 subsamples Also , divided sample into growth funds and found similar results Also, used 1-year subsamples rather than 2-year Similar, but weaker, support for the repeat winners hypothesis

49. Other Studies Malkiel argues that while repeat winners phenomenon existed in 1970s, it was not present during 1980s Carhart finds that winning funds tend to have a winning performance the following year, but not afterwards Losers have a strong tendency to persist with the worst performers persisting for years

50. The Bottom Line About Portfolio Performance Measures To adequately evaluate a portfolio, must analyze both risk and return SHARPE measures risk-premium per unit of total risk TREYNOR measures risk-premium per unit of systematic risk Jensen’s alpha measures risk-adjusted returns for both portfolios and individual assets All three measures tend to rank mutual funds similarly, but not always exactly Additional tools are available for measuring a manager’s market timing skills

51. The Bottom Line About mutual fund investments Average American buying round lots can afford only about 7 different stocks Not enough to minimize diversifiable risk Mutual funds are usually able to reduce their diversifiable risk Investors can maintain their desired risk-class by mutual fund investing Most investors should focus on a mutual fund’s fees and favor funds charging smallest fees