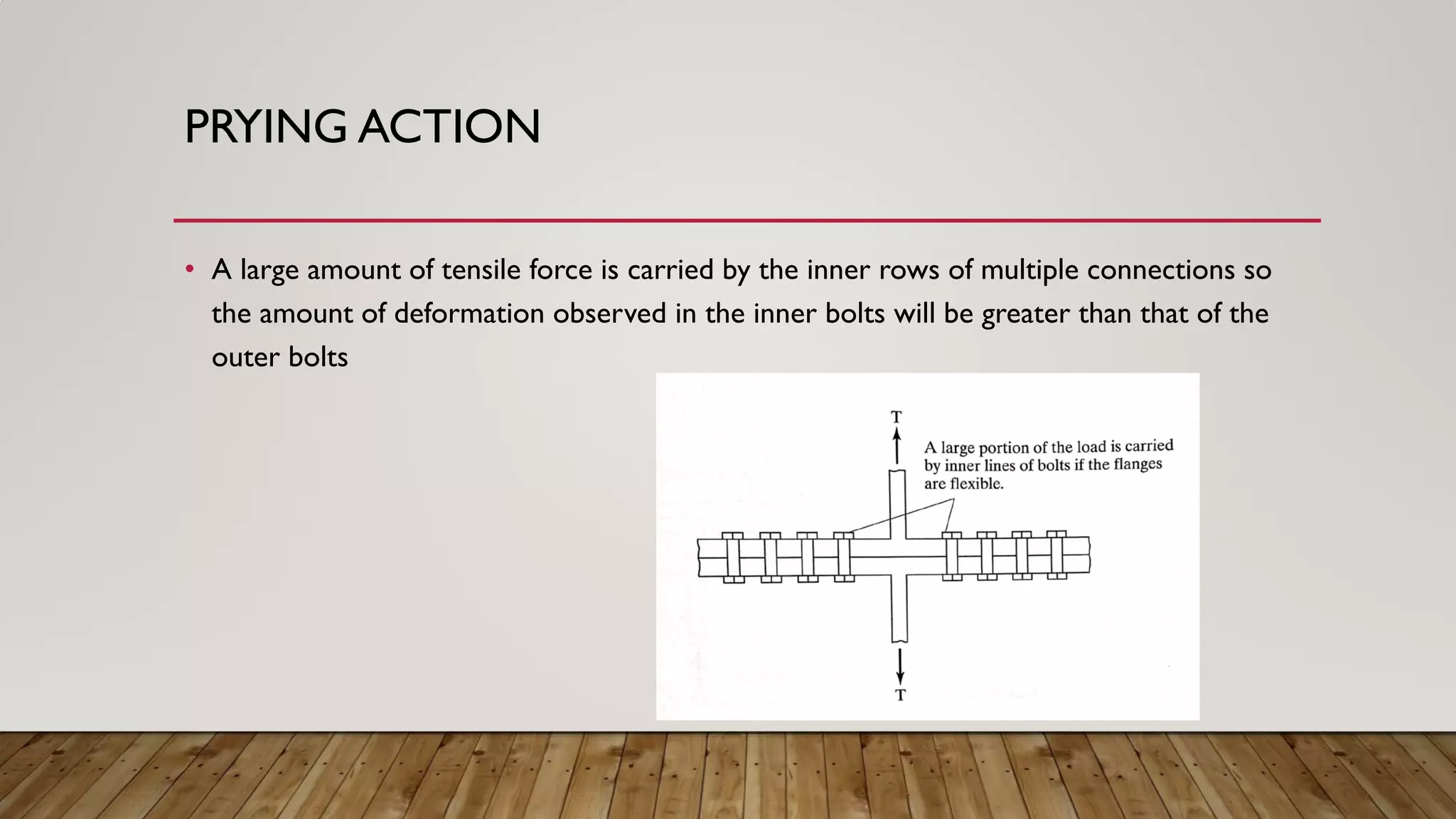
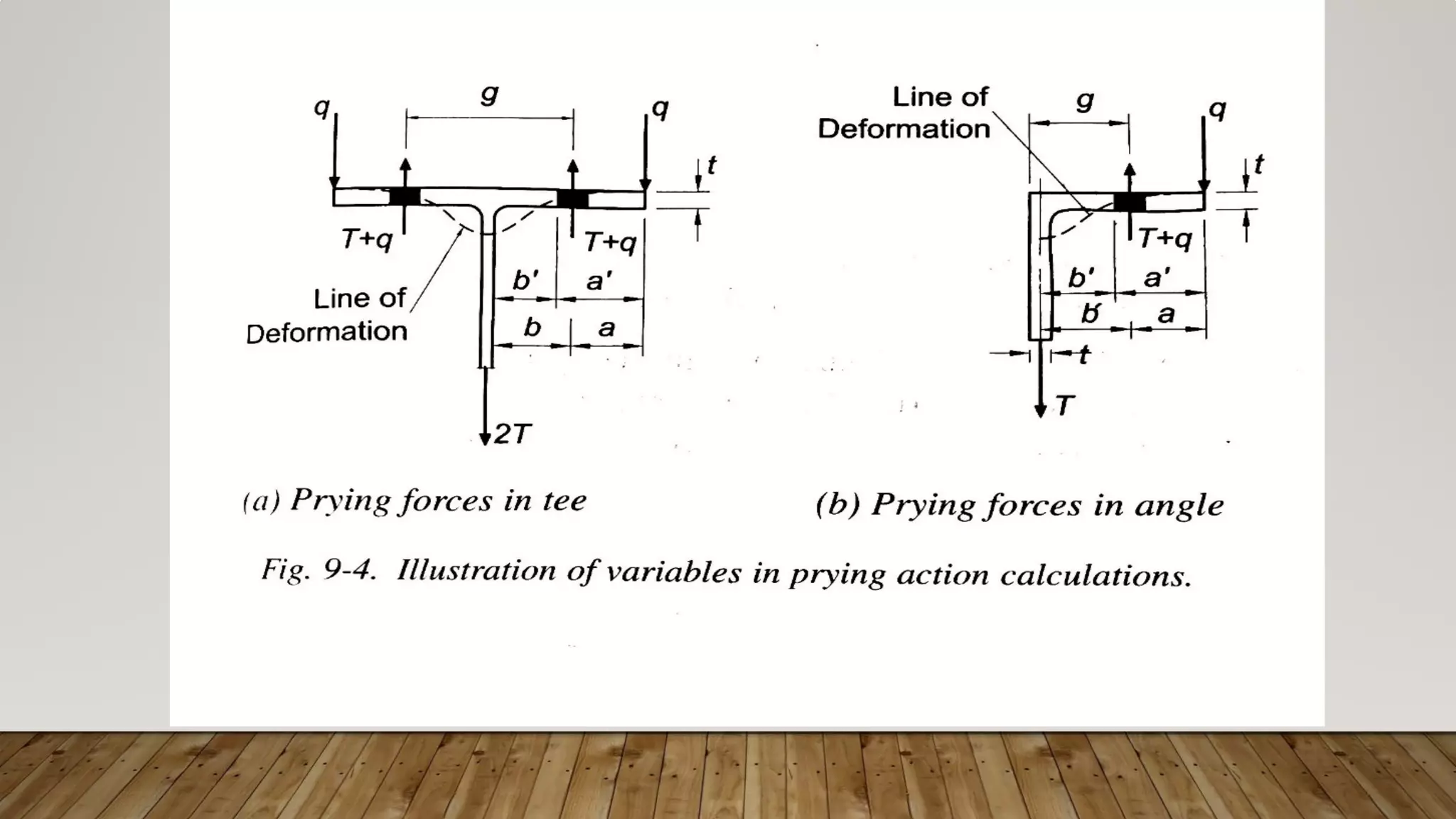
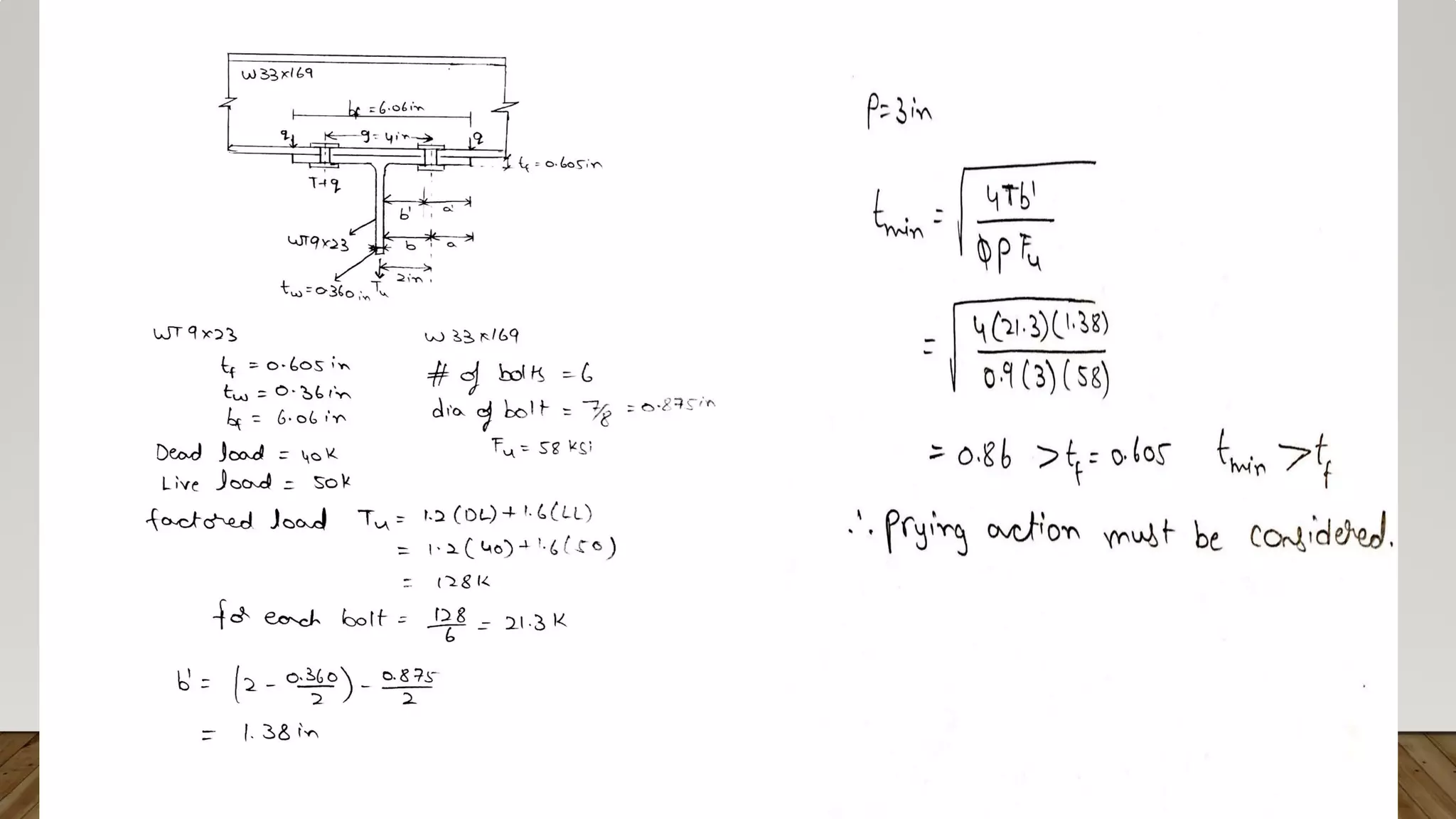
This document discusses prying action in bolted steel connections. Prying action occurs when the deformation of connected elements under tension increases the tensile force in bolts. It is affected by the strength and stiffness of the connection. The document outlines how to design for prying action by ensuring sufficient bolt diameter, fitting thickness, and distance between bolts. It provides examples calculating the required thickness to prevent prying action. It concludes that prying forces should be considered in design and sufficient rigidity of connected elements is most important.

1. PRYING ACTION
ARCH 6343
REPORT #2
ABISHEK KOPPOLU

2. OUTLINE
Prying action definition
Prying forces in Tee and Angle sections
Design for Prying action
Example 1
Example 2
conclusions

3. PRYING ACTION
• Prying action is a phenomenon (in bolted construction only) whereby the deformation
of a fitting under a tensile force increases the tensile force in the bolt.
• It is primarily a function of the strength and stiffness of the connection elements.
• It is caused by the prying forces which results in distortion of cap plates beam flanges
and bolts.

4. PRYING ACTION
• A large amount of tensile force is carried by the inner rows of multiple connections so
the amount of deformation observed in the inner bolts will be greater than that of the
outer bolts

6. DESIGN FOR PRYING ACTION
• Design for prying action include the section of bolt diameter and fitting thickness such
that there is sufficient strength in the connecting element and bolt.
• The minimum thickness required to eliminate prying action is determined by AISC steel
code book given on page 9-10.

7. • Fu= specified minimum tensile strength of connecting element, ksi
• T= required strength, rut or rat per bolt, kips
• b’ = (b-db/2)
• b =for tee type connecting element, the distance from bolt centerline to the face of the tee stem, in; for angle type
the distance from bolt centerline to centerline of leg, in
• db= bolt diameter, in
• p= tributary length per pair of bolts (perpendicular to the plane of paper) preferably not > g; maximum= 2b

8. EXAMPLE 1
• A 10 inch longWT9x 23 is connected to aW33x169 as shown in the figure with six 7/8
in A325 high strength bolts spaced 3 in o.c. If A36 steel is used, Fu= 58ksi, is the flange
sufficiently thick if prying action is considered? Given loads Pd = 40k and Pl =50k

10. DESIGN FOR PRYING ACTION
• The thickness required to ensure an acceptable combination of fitting strength and stiffness and bolt strength ,tmin
can be determined as
• ∂ = 1-(d’/p)= ratio of the net length at bolt line to gross length at the face of the stem or leg of angle.
• α‘ = 1.0 if β >= 1.0 ; the lesser of 1 and [1/ ∂ (β /1- β )] if β <1.0
• β = 1/ Þ (B/T -1) ; Þ = (b’/a’)
• B = available tension per bolt (from table 7-2)

11. DESIGN FOR PRYING ACTION
• Þ = (b’/a’)
• a= distance from bolt center line to edge of fitting, in
• d’= width of hole along the length of the fitting, in

12. Example 2
• Check weather the connected hanger section has sufficient flange thickness to ensure an
acceptable combination of fitting strength and stiffness and bolt strength to withstand
prying forces for the given loading conditions

15. DESIGN FOR PRYING ACTION
• If tmin<=t the preliminary fitting thickness is satisfactory. Otherwise fitting with a thicker
flange or change in geometry (ie.., b and p is required)
• The prying force per bolt ‘q’ can be determined as
tc = flange or angle thickness required to develop the available strength of bolt, B with no prying action

16. DESIGN FOR PRYING ACTION
• The actual determination of prying forces is quite complex and research on this subject
is still being conducted.
• The most important thing in design is the use of rigid flanges.
• Rigidity is more important than bending resistance.To achieve this the distance ‘b’ must
be as small as possible .

17. DESIGN FOR PRYING ACTION
• The minimum value of ‘b’ should be equal to the
space required to use a wrench for tightening the bolts.
• Wrench clearance dimensions are presented in
tables 7-16 of AISC manual under
“Entraining and tightening clearance.”

18. CONCLUSIONS
• Prying forces should be considered in designing of bolted connection of steel structures
to prevent distortion of bolts and flanges
• Prying force need to be taken into account for the increase in tension of bolts.
• Prying action could be a concern where deflections are major serviceable criteria.
• Sufficient distance ‘b’ should be maintained to make the flange rigid than more bending
resistant.

19. REFERENCES
• Structural steel design fifth edition, Jack C. McCormac and Stephen F. Csernak.
• AISC Steel manual 14th edition
• http://ceprofs.tamu.edu/llowery/CVEN446/ClassNotes13a/446Class38.PDF
• Steel structures design and behavior by Salmon, Jhonson