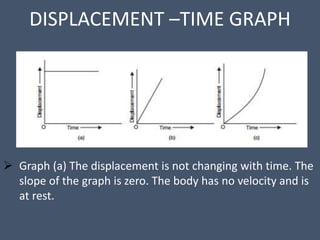
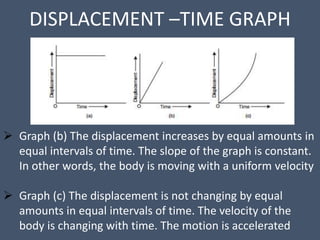
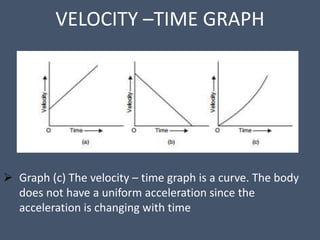
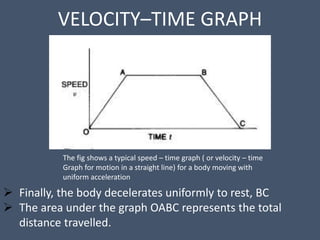
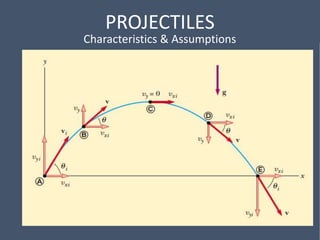
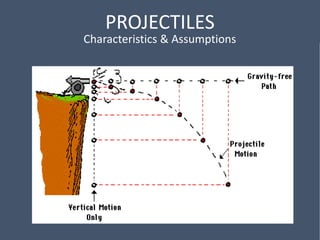
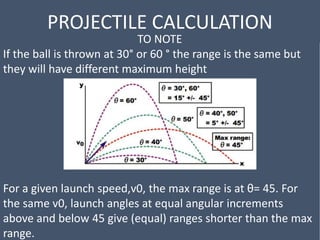
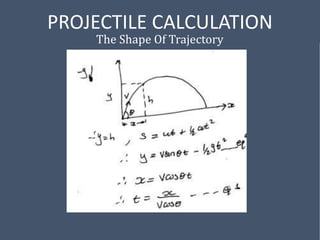
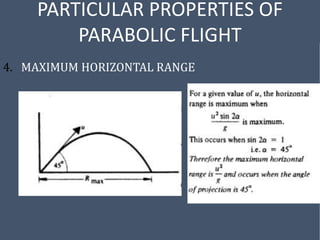
This document provides an overview of mechanical science concepts related to linear motion. It defines key terms like displacement, velocity, acceleration, and discusses displacement-time and velocity-time graphs. Uniform acceleration equations of motion are derived. Gravity is described as causing uniform acceleration. Projectile motion is analyzed by resolving velocities into horizontal and vertical components. Examples demonstrate calculating projectile range and maximum height.

1. MECHANICAL SCIENCE
(MEC-MES 121)
LINEAR MOTION

2. CONTENTS
 INTRODUCTION
 BASIC TERMS
 DISPLACEMENT –TIME GRAPH
 VELOCITY –TIME GRAPH
 EQUATIONS OF MOTION UNDER UNIFORM ACCELERATION
(Bodies moving with uniform acceleration)
 MOTION UNDER THE EFFECTS OF GRAVITY
 COMBINATION AND RESOLUTION OF VELOCITIES
 PROJECTILES

3. INTRODUCTION
 A body is said to be in motion if it changes its position
with respect to its surroundings
 The nature of the path of displacement of various
particles of a body determines the type of motion.
The motion may be of the following types:
A. Rectilinear translation (straight line motion)
B. Curvilinear translation (the particles of a body move
along circular arcs or curved paths)
C. Rotary or circular motion (a body move along
concentric circles and the displacement is measured in
terms of angle in radians or revolutions)

4. BASIC TERMS
1. DISPLACEMENT -is the distance in a straight line between
the start and end points of some motion.
2. DISTANCE is the length along the path of an object,
whatever the form of the path.
3. SPEED is the rate at which distance is covered.
4. AVERAGE SPEED is the distance covered in a time interval
divided by the time taken
5. VELOCITY is the rate at which displacement along a
straight line changes with time.

5. BASIC TERMS
6. AVERAGE VELOCITY is the displacement along a straight
line occurring in a time interval divided by that time
7. ACCELERATION is the rate of change of velocity with time
8. AVERAGE ACCELERATION is the change of velocity
occurring over a time interval divided by the time
9. A CONSTANT OR UNIFORM ACCELERATION occurs when
the velocity changes by equal amounts in equal intervals
of time

6. DISPLACEMENT –TIME GRAPH
 Graph (a) The displacement is not changing with time. The
slope of the graph is zero. The body has no velocity and is
at rest.

7. DISPLACEMENT –TIME GRAPH
 Graph (b) The displacement increases by equal amounts in
equal intervals of time. The slope of the graph is constant.
In other words, the body is moving with a uniform velocity
 Graph (c) The displacement is not changing by equal
amounts in equal intervals of time. The velocity of the
body is changing with time. The motion is accelerated

8. VELOCITY –TIME GRAPH
 Graph (a) The velocity of the body increases linearly with
time. In other words, the acceleration of the body is
constant
 Graph (b) The body has a finite initial velocity. As the time
passes, the velocity decreases linearly with time until its
final velocity is zero i.e it comes to rest. Thus, the body has
a constant deceleration (or retardation) as the slope is -ve

9. VELOCITY –TIME GRAPH
 Graph (c) The velocity – time graph is a curve. The body
does not have a uniform acceleration since the
acceleration is changing with time

10. VELOCITY–TIME GRAPH
 Uniform acceleration from rest to maximum speed is
shown by OA;
 The speed is maintained constant at the maximum value,
shown by AB;
The fig shows a typical speed – time graph ( or velocity – time
Graph for motion in a straight line) for a body moving with
uniform acceleration

11. VELOCITY–TIME GRAPH
 Finally, the body decelerates uniformly to rest, BC
 The area under the graph OABC represents the total
distance travelled.
The fig shows a typical speed – time graph ( or velocity – time
Graph for motion in a straight line) for a body moving with
uniform acceleration

12. EQUATIONS OF MOTION UNDER
UNIFORM ACCELERATION
Then;
the change in velocity in the time interval t is (v - u). Hence
the acceleration a is (v - u)/t. Rearranging this gives:

13. EQUATIONS OF MOTION UNDER
UNIFORM ACCELERATION
The distance S which the body travels in time t is determined
as follows:
Since the acceleration is uniform i.e the velocity changes by
an equal amount in equal intervals of time, therefore;

14. EQUATIONS OF MOTION UNDER
UNIFORM ACCELERATION

15. EQUATIONS OF MOTION UNDER
UNIFORM ACCELERATION
OR

16. SUMMARY OF FORMULAE FOR
UNIFORM ACCELERATION
Where;
=

17. EXAMPLES
EXAMPLE 1
ANSWER 7.125KM
EXAMPLE 2
𝑎 = 1.4 𝑚/𝑠2
t = 4.9 s v = 23.7 m/s

18. VECTORS
 Velocity and acceleration are vector quantities
 A vector quantity is one for which both its magnitude and
direction have to be stated for its effects to be
determined; they have to be added by methods which
take account of their directions, e.g. the parallelogram
method.

19. Example
 A projectile is thrown vertically upwards with a velocity of
10 m/s. If there is a horizontal wind blowing at 5 m/s, what
will be the velocity with which the projectile starts out?
SOLUTION
 Figure above shows the vectors representing the two
velocities and their resultant, i.e. sum, determined from
the parallelogram of vectors.

20. EXAMPLE cont..
 We can use a scale drawing to obtain the resultant or,
because the angle between the two velocities is 90° we
can use the Pythagoras theorem
Hence v = 11.2 m/s.
 This velocity will be at an angle θ to the horizontal, where
tan θ = 10/5 and so θ = 63.4°.

21. RESOLUTION INTO COMPONENTS
 A single vector can be resolved into two components at
right angles to each other by using the parallelogram
method
 For example, a velocity v at an angle θ to the horizontal
can be resolved into a;
horizontal component of v cos θ
and
vertical component of v sin θ

22. EXAMPLE
 A projectile is fired from a gun with a velocity of 200 m/s
at 30° to the horizontal. What is (a) the horizontal velocity
component, (b) the vertical velocity component?
(a) Horizontal component = v cos θ = 200 cos 30°= 173 m/s.
(b) Vertical component = v sin θ = 200 sin 30° = 100 m/s.

23. MOTION UNDER THE EFFECTS OF
GRAVITY
 Before the time of Galileo it was thought that if two
objects of different masses were dropped, the heavier
object would fall fast than the light one
 In a famous series of experiments Galileo showed that this
was not true.
 If air resistance is ignored, all freely falling objects in a
vacuum, fall with the same uniform acceleration directed
towards the surface of the earth as a result of a
gravitational force acting between the object and the
earth.

24. MOTION UNDER THE EFFECTS OF
GRAVITY
 This acceleration is termed the acceleration due to
gravity g.
 For most practical purposes, the acceleration due to
gravity at the surface of the earth is taken as being 9.81
m/s2.

25. MOTION UNDER THE EFFECTS OF
GRAVITY
 The equations for motion of a falling object are those for
motion in a straight line with the acceleration as g.

26. EXAMPLE
HEIGHT = 3.27m t = 0.82 S

27. EXAMPLE

28. PROJECTILES
 A projectile is a particle which is given an initial velocity
and then moves under the action of its weight only.
 For example, a ball which is thrown is a projectile and we
are concerned with its flight from the moment it leaves
the thrower’s hand until its flight is interrupted
 If the initial velocity of a projectile is vertical it will move in
a straight line
 If the initial velocity is not vertical the particle will move in
a curve and its flight can be analyzed by considering the
vertical and horizontal components of its acceleration,
velocity and displacement

29. PROJECTILES
Characteristics & Assumptions
 Planar motion
 Air resistance: negligible
 Gravity: downward
 No horizontal acceleration
 Constant vertical acceleration
 Parabolic trajectory
 Independent horizontal and vertical motions

30. PROJECTILES
Characteristics & Assumptions
 Since velocity is a vector, velocity may therefore be
resolved into vector components.
 Projectiles will have velocities both in the vertical and
horizontal directions.
 Hence at each instant the velocity of a projectile may be
resolved into two components - vertical and horizontal
 With these assumptions, an object in projectile motion will
follow a parabolic path,This path is called the trajectory

31. PROJECTILES
Characteristics & Assumptions

32. PROJECTILES
Characteristics & Assumptions

33. PROJECTILE CALCULATION
 Example 1 of a ball which has been projected at an angle θ
from the ground. Calculate the distance travelled/Range
and the maximum point above the ground attained by the
ball
SOLUTION
 If given v, θ, g, then d and h can be easily calculated.

34. PROJECTILE CALCULATION
SOLUTION cont…
 The trick is to look at the initial conditions of velocity and
direction (θ).
 Therefore, we can start by resolving the velocity into its
components

35. PROJECTILE CALCULATION
SOLUTION cont…
 Note; The components act independently, therefore, you
can calculate what happens in the vertical or horizontal
entirely independent then you can bring them together to
get your solution.
 For this example, let us assume that;
v = 20 m/s
θ =30°
g = 9.81 𝑚 𝑠2

36. PROJECTILE CALCULATION
SOLUTION cont…
∴ 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 = 𝑣𝑠𝑖𝑛𝜃 = 20𝑠𝑖𝑛30 = 10 𝑚/𝑠
𝑡ℎ𝑒𝑛 ℎ𝑜𝑟𝑖𝑧𝑜𝑛𝑡𝑎𝑙 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 = 𝑣𝑐𝑜𝑠𝜃 = 20𝑐𝑜𝑠30
= 17.32 𝑚/𝑠
TREATING THE VERTICAL COMPONENT ALONE
 The vertical component will make an object to go up and
back again

37. PROJECTILE CALCULATION
SOLUTION cont…
TREATING THE VERTICAL COMPONENT ALONE
 𝑣 = 0
 The question is, how long does it take to go up and back
again
∴ 𝑤𝑒 𝑐𝑎𝑛 𝑢𝑠𝑒 𝑣 = 𝑢 + 𝑎𝑡 𝑤ℎ𝑒𝑟𝑒,
𝑣 = 𝑓𝑖𝑛𝑎𝑙 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 𝑤ℎ𝑖𝑐ℎ 𝑖𝑠 = 0
𝑢 = 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 = 10 m/s
𝑎 = −𝑔

38. PROJECTILE CALCULATION
SOLUTION cont…
TREATING THE VERTICAL COMPONENT ALONE
∴ 0 = 10 − 𝑔𝑡 = 10 − 9.81𝑡
∴ 𝑡 = 1 𝑠𝑒𝑐𝑜𝑛𝑑
 It means that it takes 1 second for the ball to reach the
top, similarly, it takes 1 second from the top to the ground
∴ 𝑡ℎ𝑒 𝑡𝑜𝑡𝑎𝑙 𝑡𝑖𝑚𝑒 𝑓𝑜𝑟 𝑡ℎ𝑒 𝑏𝑎𝑙𝑙 𝑡𝑜 𝑔𝑜 𝑢𝑝 𝑎𝑛𝑑 𝑑𝑜𝑤𝑛 𝑖𝑠
2 𝑠𝑒𝑐𝑜𝑛𝑑𝑠

39. PROJECTILE CALCULATION
SOLUTION cont…
TREATING THE HORIZONTAL COMPONENT ALONE
Now, in those 2 seconds the ball is travelling with a
horizontal component which is v cos θ
And the distance it will travel will be
 ∴ 𝑑 = 𝑣 cos 𝜃 t
 Note; Gravity doesn’t affect horizontal component, ∴ 𝑔 = 0

40. PROJECTILE CALCULATION
SOLUTION cont…
TREATING THE HORIZONTAL COMPONENT ALONE
s𝑖𝑛𝑐𝑒 𝑑 = 𝑣 cos 𝜃 t
∴ 𝑑 = 17.32 × 2 = 34.64 𝑚
Therefore, the ball will go a distance of 34.64 m as its range.

41. PROJECTILE CALCULATION
SOLUTION cont…
NOW WE WANT TO KNOW HOW HIGH THE BALL
WENT AT ITS MAXIMUM HEIGHT
∴ 𝑓𝑜𝑟 𝑡ℎ𝑎𝑡 𝑤𝑒 𝑛𝑒𝑒𝑑 𝑡ℎ𝑒 𝑓𝑜𝑟𝑚𝑢𝑙𝑎; 𝑣2 = 𝑢2 + 2aS
𝑣 = 0 (𝑇ℎ𝑒 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 𝑎𝑡 𝑡ℎ𝑒 𝑡𝑜𝑝)
𝑢 = 10 𝑚 𝑠 (initial velocity)
∴ 0 = 102 − 2 9.81 𝑆
∴ 𝑆 = 5𝑚

42. PROJECTILE CALCULATION
TO NOTE
If the ball is thrown at 30° or 60 ° the range is the same but
they will have different maximum height
For a given launch speed,v0, the max range is at θ= 45. For
the same v0, launch angles at equal angular increments
above and below 45 give (equal) ranges shorter than the max
range.

43. PROJECTILE CALCULATION
 Example 2, Sometimes we may want to know conditions
at any point P of the trajectory e.g. height of point P, the
distance covered by point P and the new velocity
 But they will be another point when the height will also
be h and that is point therefore, you will have two
solutions to choose from
d

44. PROJECTILE CALCULATION
Example 2 solution
 Resolving the initial conditions first,
d

45. PROJECTILE CALCULATION
Example 2 solution cont
Considering vertical motion;
∴ 𝑤𝑒 𝑐𝑎𝑛 𝑢𝑠𝑒 𝑆 = 𝑢𝑡 +
1
2
𝑎𝑡2……equation 1
𝑤ℎ𝑒𝑟𝑒 𝑆 = ℎ (ℎ𝑒𝑖𝑔ℎ𝑡 𝑜𝑓 𝑝𝑜𝑖𝑛𝑡 𝑝)
𝑢 = 𝑖𝑛𝑖𝑡𝑖𝑎𝑙 𝑣𝑒𝑙𝑜𝑐𝑖𝑡𝑦 𝑖𝑛
𝑡ℎ𝑒 𝑣𝑒𝑟𝑡𝑖𝑐𝑎𝑙 𝑑𝑖𝑟𝑒𝑐𝑡𝑖𝑜𝑛
Substituting the vertical component into equation 1 gives
∴ ℎ = 𝑣𝑠𝑖𝑛𝜃𝑡 −
1
2
𝑔𝑡2
…eguation 2
The 𝑡2 will give two solutions for h of and h of
Therefore, the period of time will determine the required
position of P.

46. PROJECTILE CALCULATION
Example 2 solution cont
Now considering Horizontal motion;
If variables t and v are known then the position
of and therefore, we will say;
∴ 𝑑 = 𝑣𝑡
𝑑 = 𝑣𝑐𝑜𝑠𝜃𝑡 ……equation 3
If one of the variables is not given it subject of the formula
from equation 3 and substitute in equation 2 e.g t
∴ 𝑡 =
𝑑
𝑣𝑐𝑜𝑠𝜃
Then ℎ =
𝑣𝑑𝑠𝑖𝑛𝜃
𝑣𝑐𝑜𝑠𝜃
−
1
2
𝑔(
𝑑
𝑣𝑐𝑜𝑠𝜃
)2

47. PROJECTILE CALCULATION
Example 2 solution cont
Then ℎ =
𝑣𝑑𝑠𝑖𝑛𝜃
𝑣𝑐𝑜𝑠𝜃
−
1
2
𝑔(
𝑑
𝑣𝑐𝑜𝑠𝜃
)2
Therefore, ℎ = dtanθ −
1
2
𝑔𝑑2𝑠𝑒𝑐2𝜃
𝑣2
Given values of h,θ, v, g therefore the solution will have two
solutions of d for point and but we want the
position of point therefore, we will take the shorter
distance.

48. PROJECTILE CALCULATION
Example 2 solution cont
Finding new velocity 𝑣∗ at point P;
 Horizontal component does not change as it is not
affected by gravity
 ∴ Horizontal component = vcosθ
 Now vertical component v p = 𝑢 + 𝑎𝑡
v p = 𝑣𝑠𝑖𝑛𝜃 − 𝑔𝑡

49. PROJECTILE CALCULATION
Example 2 solution cont
Finding new velocity 𝑣∗ at point P;
∴ = 𝑣𝑠𝑖𝑛𝜃 − 𝑔𝑡 is the new vertical component at point p
Now combining the two
∴ 𝑣∗2 = (𝑣𝑐𝑜𝑠𝜃)2 + (𝑣𝑠𝑖𝑛𝜃 − 𝑔𝑡)2
Then finding the new angle
𝑡𝑎𝑛𝜃∗=
𝑣𝑠𝑖𝑛𝜃−𝑔𝑡
𝑣𝑐𝑜𝑠𝜃

50. PROJECTILE CALCULATION
The Shape Of Trajectory

51. PROJECTILE CALCULATION
The Shape Of Trajectory
𝑦 = x tanθ −
1
2
𝑔𝑥2𝑠𝑒𝑐2𝜃
𝑣2
This is the equation of a trajectory/path/parabola

52. PROJECTILE CALCULATION
Example 3
What is the velocity or angle of the ball that is necessary to
get over the wall of 4m high at B?
𝑑 = 𝑣𝑡
∴ 20 = 𝑣𝑐𝑜𝑠𝜃𝑡
Then vertical motion
𝑆 = 𝑢𝑡 +
1
2
𝑎𝑡2
∴ 4 = 𝑣𝑠𝑖𝑛𝜃𝑡 −
1
2
𝑔𝑡2

53. PROJECTILE CALCULATION
Example 3 cont..
∴ 4 = 𝑣𝑠𝑖𝑛𝜃𝑡 −
1
2
𝑔𝑡2
Now because of 𝑡2
you will find two solutions for A and B
but you want a solution at B therefore you will choose from
the two solutions found.
𝑡=
20
𝑣𝑐𝑜𝑠𝜃
Then by substitution,
∴ ℎ =
𝑣𝑑𝑠𝑖𝑛𝜃
𝑣𝑐𝑜𝑠𝜃
−
1
2
𝑔(
𝑑
𝑣𝑐𝑜𝑠𝜃
)2
4 = 20tanθ −
1
2
𝑔202𝑠𝑒𝑐2𝜃
𝑣2 , if given θ then the required
velocities can be calculated or if given velocity then θ will

54. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
 Certain information about projectiles is required
frequently
 Consider a particle which is projected from a point O on
a level ground with a velocity u at an angle 𝛼 to the
horizontal, reaching ground level again at a point A

55. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
1. TIME OF FLIGHT
This is the time taken for the particle to travel along
its path from O to A.
Where y is the
vertical distance

56. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
2. GREATEST HEIGHT; this is h in the diagram
Where is the final
velocity

57. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
3. HORIZONTAL RANGE; this is the distance from the
initial position to the final position on a horizontal
plane through the point of projection i.e OA.
Where tp is the time
at the top
O
A
Where Sx is the distance in
the x or horizontal direction
R = Horizontal Range
tf = time of flight

58. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
3. HORIZONTAL RANGE
To find time of flight
By substitution
Since 2cosθsinθ = sin2θ
θ

59. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
4. MAXIMUM HORIZONTAL RANGE

60. PARTICULAR PROPERTIES OF
PARABOLIC FLIGHT
5. ANGLE OF PROJECTION REQUIRED TO ACHIEVE A
GIVEN HORIZONTAL RANGE Ro (Ro<Rmax)

61. Worked problems
EXAMPLE 1
EXAMPLE 2
EXAMPLE 3
A train traveling along a straight line with constant acceleration is observed to travel
consecutive displacements of 1.2 km in times of 30 𝑠 and 60 𝑠 respectively. Find the
initial velocity of the train.

62. SOLUTION 1

63. SOLUTION 1 CONT..

64. SOLUTION 2

65. SOLUTION 2 CONT..