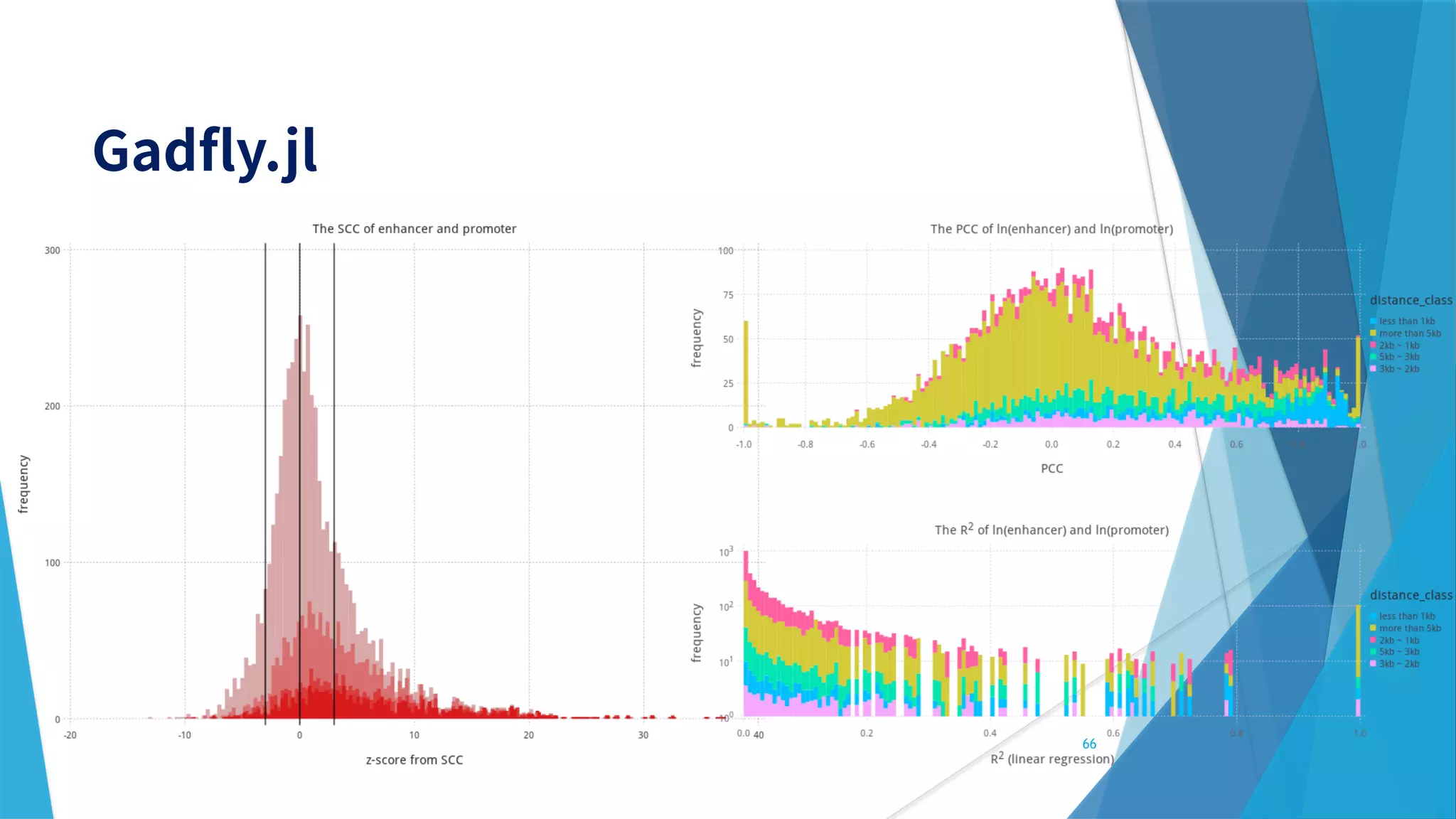
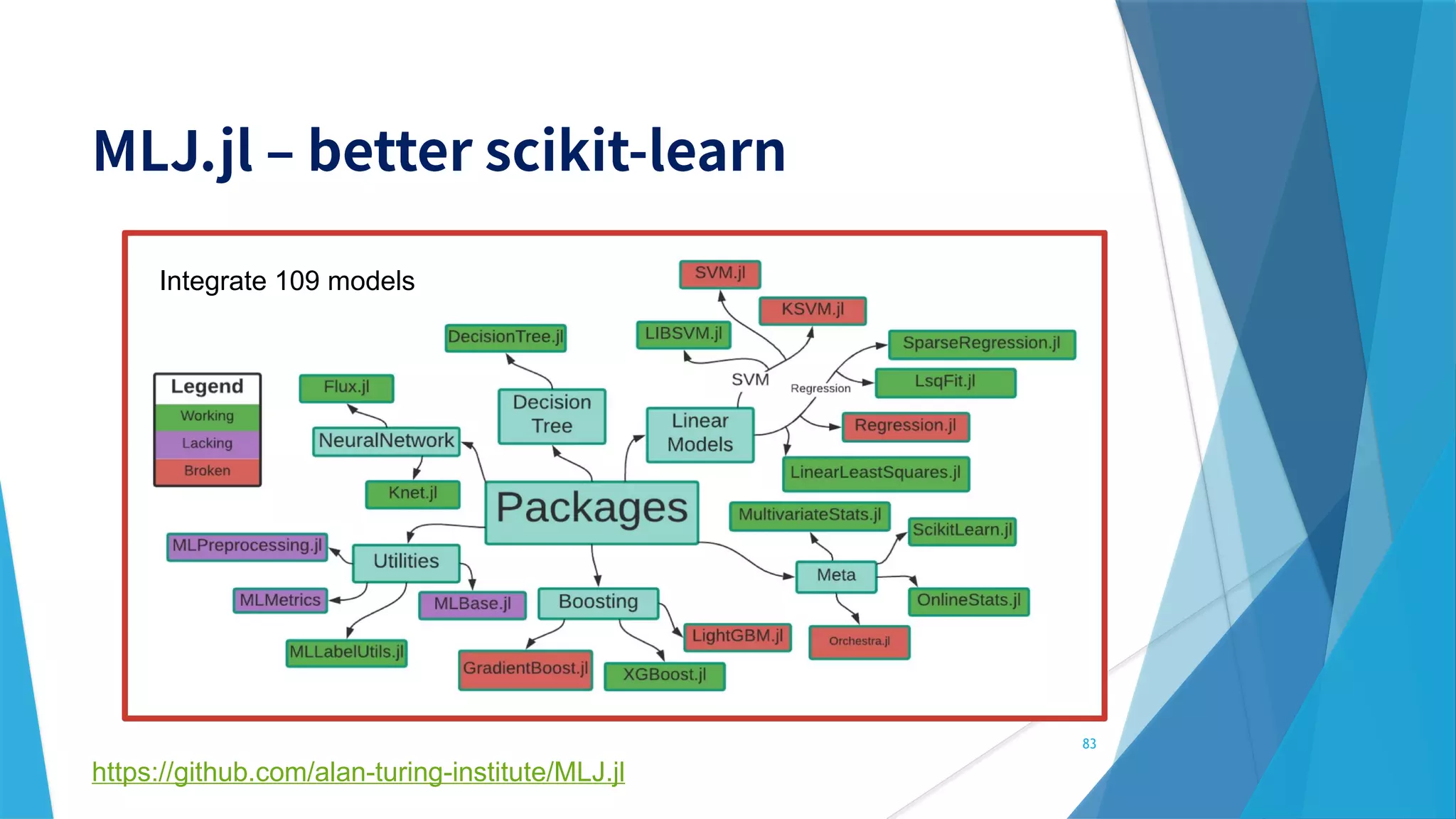
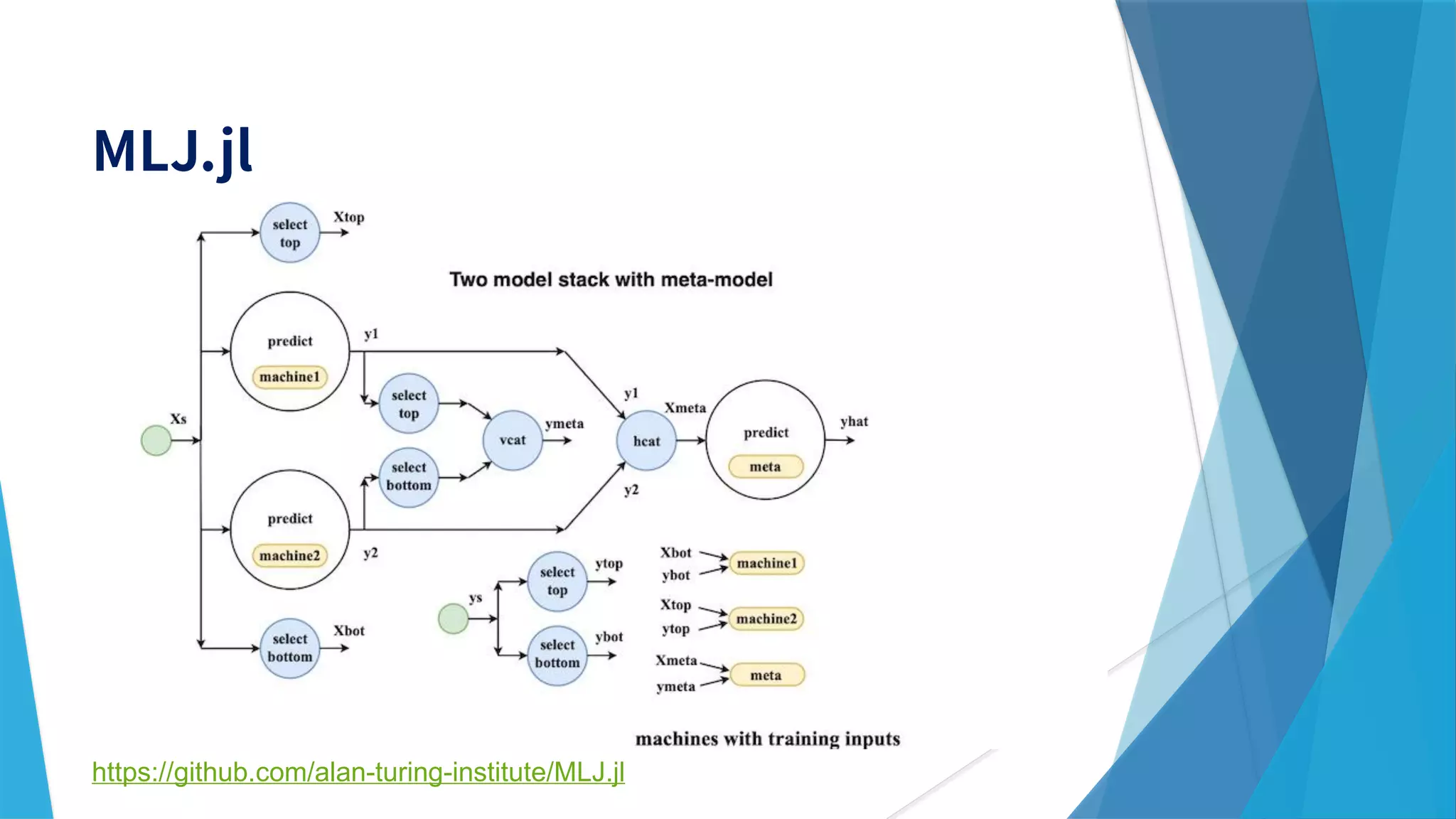
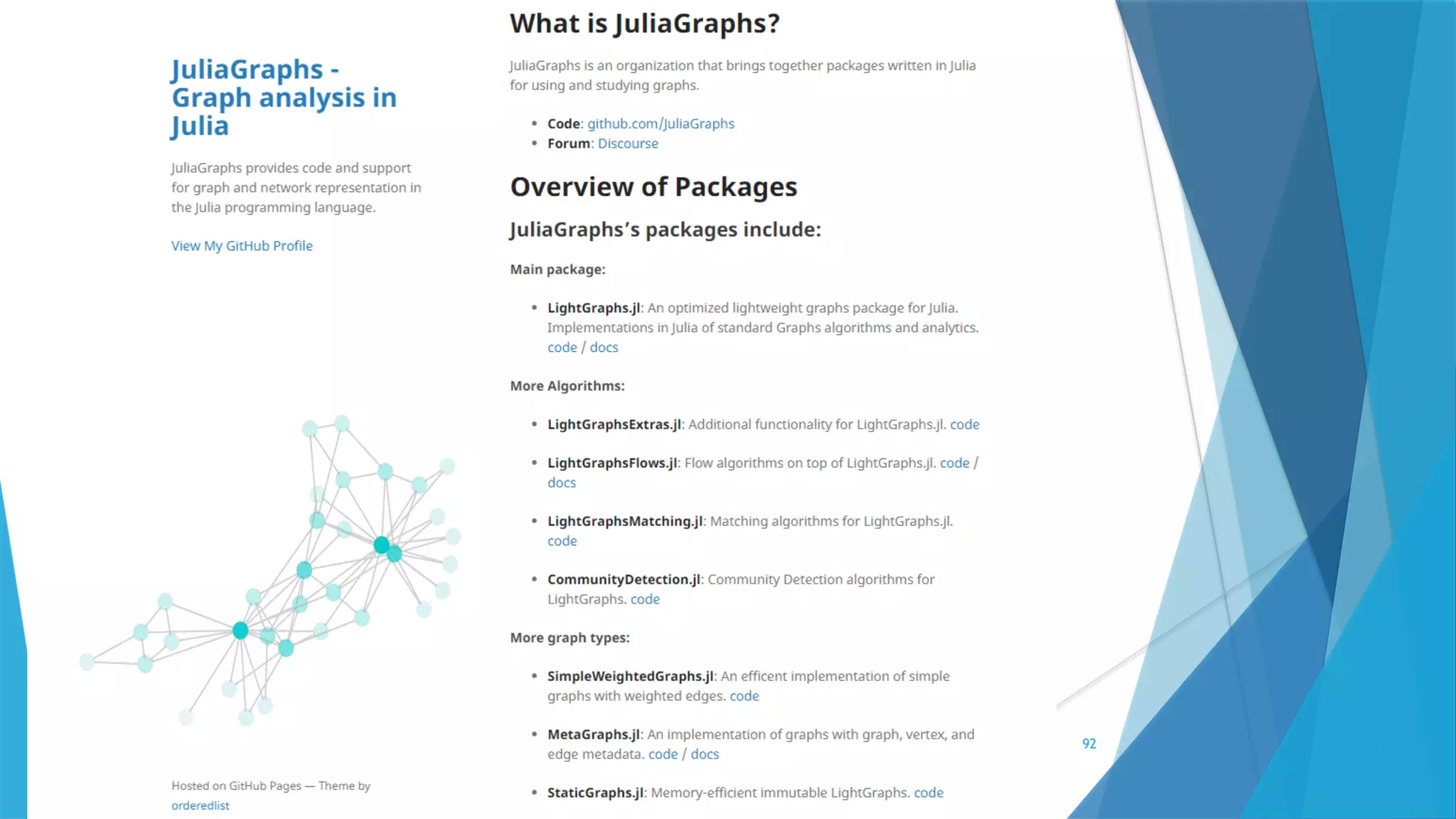
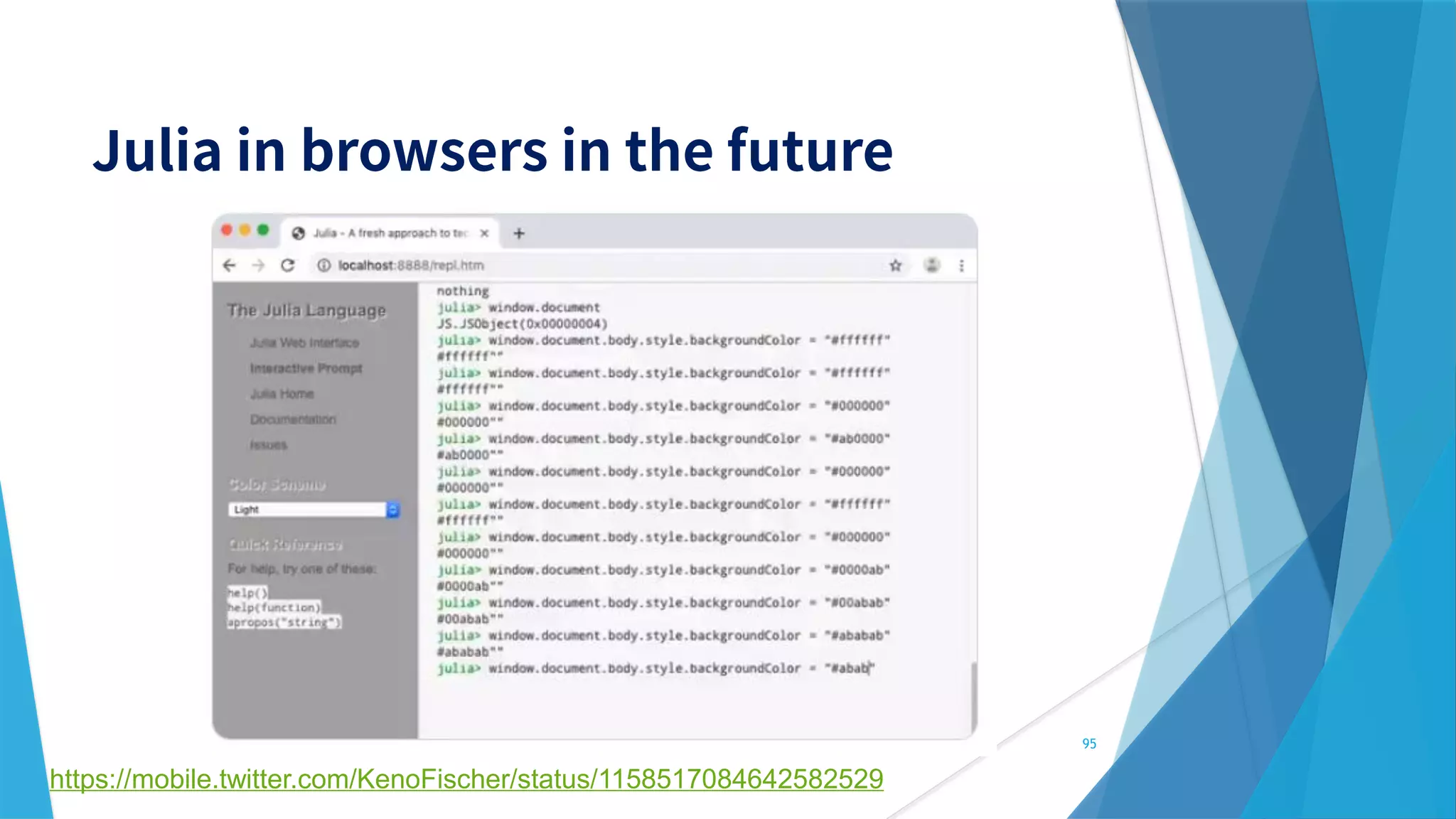
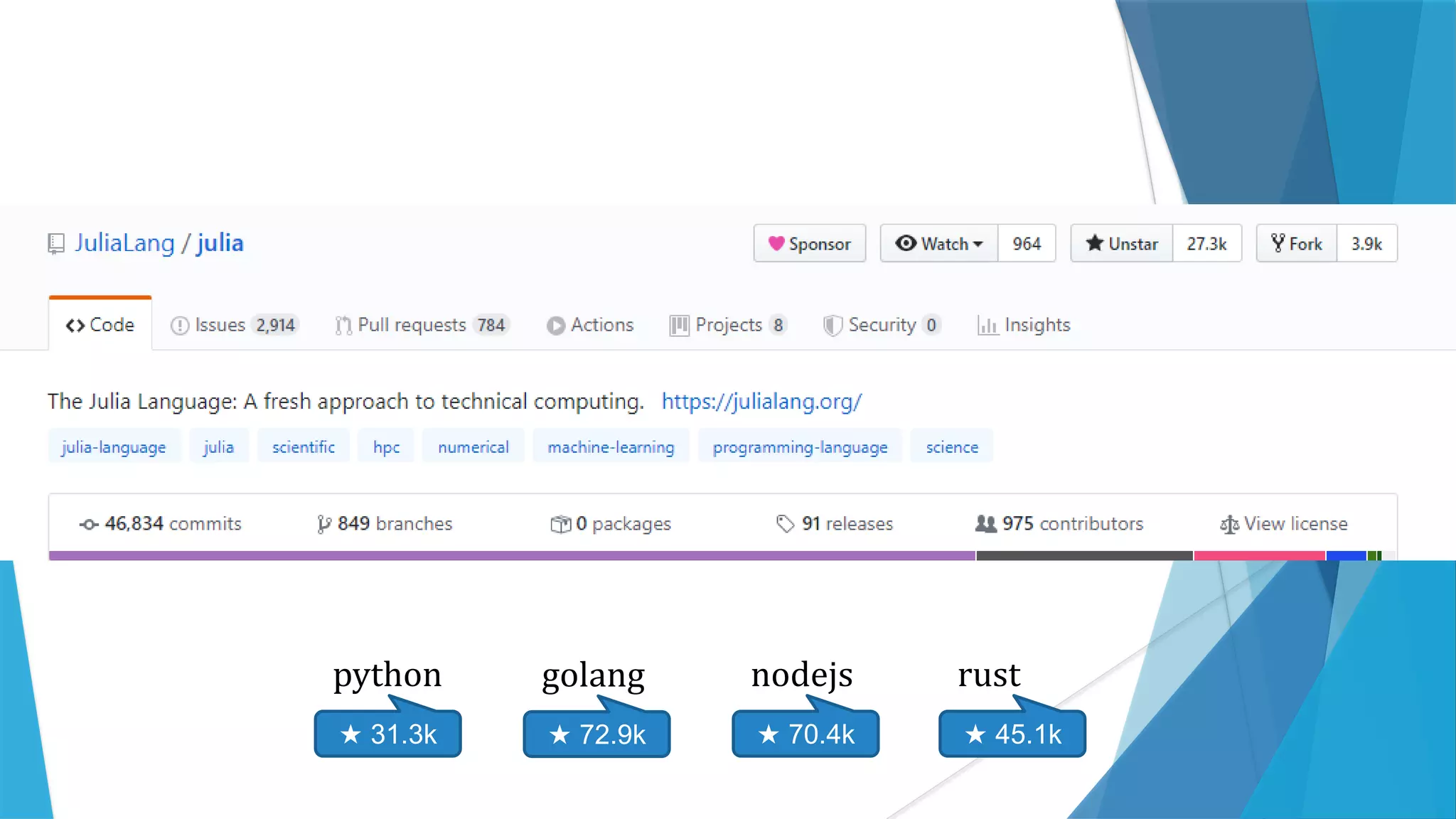
This document provides information about the Julia programming language. It discusses Julia's popularity, use cases in various fields like robotics and finance, benchmarks, and key features. It also demonstrates Julia code examples and highlights various Julia packages and tools for scientific computing, machine learning, and more.




![a = [1, 2, 3, 4, 5]
function square(x)
return x^2
end
for x in a
println(square(x))
end
8](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-8-2048.jpg)















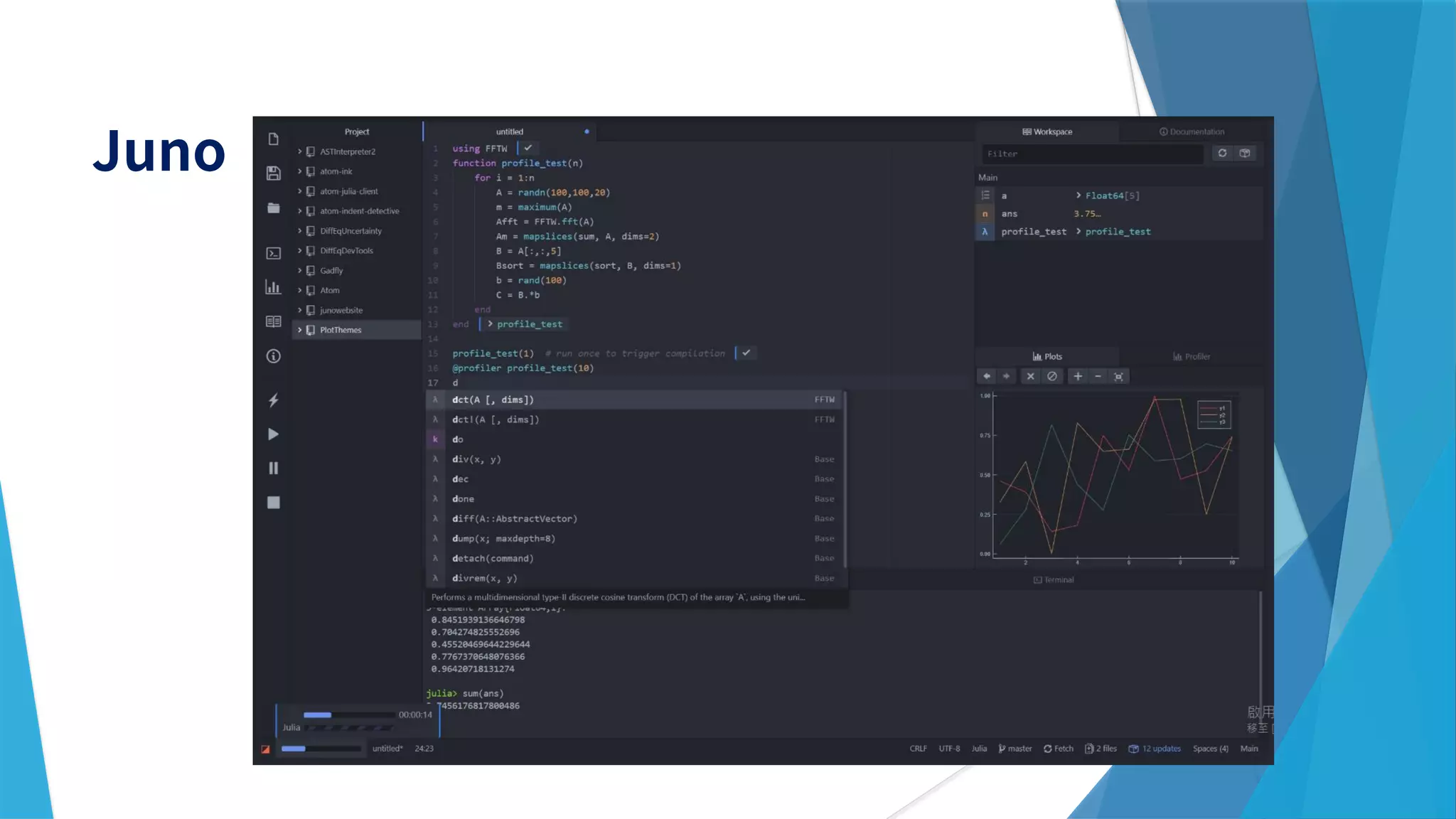






![julia> @code_native add(1, 2)
.text
Filename: REPL[2]
pushq %rbp
movq %rsp, %rbp
Source line: 2
leaq (%rcx,%rdx), %rax
popq %rbp
retq
nopw (%rax,%rax)
function add(a, b)
return a+b
end
37](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-33-2048.jpg)








![julia> using DataFrames
julia> df = DataFrame(A = 1:4, B = ["M", "F", "F", "M"])
4× 2 DataFrame
│ Row │ A │ B │
├─────┼───┼───┤
│ 1 │ 1 │ M │
│ 2 │ 2 │ F │
│ 3 │ 3 │ F │
│ 4 │ 4 │ M │
55](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-42-2048.jpg)
![julia> df[:A]
4-element Array{Int64,1}:
1
2
3
4
julia> df[2, :A]
2
56](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-43-2048.jpg)

![julia> names = DataFrame(ID = [1, 2], Name = ["John Doe",
"Jane Doe"])
julia> jobs = DataFrame(ID = [1, 2], Job = ["Lawyer",
"Doctor"])
julia> full = join(names, jobs, on = :ID)
2× 3 DataFrame
│ Row │ ID │ Name │ Job │
├─────┼────┼──────────┼────────┤
│ 1 │ 1 │ John Doe │ Lawyer │
│ 2 │ 2 │ Jane Doe │ Doctor │ 58](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-45-2048.jpg)

![63
julia> data = DataFrame(X=[1,2,3], Y=[2,4,7])
3x2 DataFrame
|-------|---|---|
| Row # | X | Y |
| 1 | 1 | 2 |
| 2 | 2 | 4 |
| 3 | 3 | 7 |](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-47-2048.jpg)

![65
julia> newX = DataFrame(X=[2,3,4]);
julia> predict(OLS, newX, :confint)
3× 3 Array{Float64,2}:
4.33333 1.33845 7.32821
6.83333 2.09801 11.5687
9.33333 1.40962 17.257
# The columns of the matrix are prediction, 95% lower and
upper confidence bounds](https://image.slidesharecdn.com/20200526thelanguageforfuturejulia-200526141151/75/Julia-The-language-for-future-49-2048.jpg)