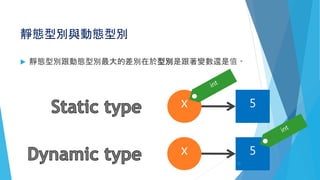
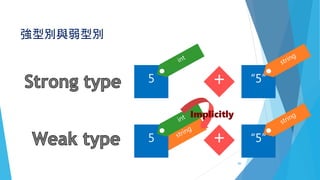
This document introduces Julia and provides an overview of its key features. It begins with introductions and background on why Julia was created. It then covers basic Julia concepts like variables, arithmetic operators, control flow, arrays, functions, and parallelization capabilities. The document also discusses Julia's built-in package ecosystem and provides examples of packages like DataFrames. It aims to provide attendees with foundational knowledge of the Julia programming language.

1. Introduction to
Julia Taiwan發起人 杜岳華
1

2. 自我介紹
 杜岳華
 疾病管制署小小研發替代役
 想成為生醫資料科學家
 陽明生醫資訊所碩士
 成大醫學檢驗生物技術系學士
 成大資訊工程系學士
2

3. Why Julia?
3

4. In scientific computing and data science…
4

5. Other users
5

6. Avoid two language problem
 One language for rapid development
 The other for performance
 Example:
 Python for rapid development
 C for performance
6

7. itertools的效能
 一篇文章描述兩者的取捨
 「一般來說，我們不會去優化所有的程式碼，因為優化有很
大的代價:一般性與可讀性。 通常跑得快與寫的快，是要做
取捨的。 這裡的例子很好想像，大家只要比較R的程式碼與
Rcpp的程式碼就好了。」
http://wush.ghost.io/itertools-performance/
7

8. 使用Julia就不用做取捨了阿!!
8

9. Julia的特色
 Write like Python, run like C.
 擁有python的可讀性 (readibility)
 擁有C的效能
 Easy to parallelism
 內建套件管理器
 ……
9

10. Julia code
a = [1, 2, 3, 4, 5]
function square(x)
return x^2
end
for x in a
println(square(x))
end
10

11. https://julialang.org/benchmarks/
Julia performance
11

12. Who use Julia?
12

13.  Nobel prize in economic sciences
 The founder of QuantEcon
 “His team at NYU uses Julia for macroeconomic modeling and contributes
to the Julia ecosystem.”
https://juliacomputing.com/case-studies/thomas-sargent.html
13

14.  In 2015, economists at the Federal Reserve Bank of New York (FRBNY)
published FRBNY’s most comprehensive and complex macroeconomic
models, known as Dynamic Stochastic General Equilibrium, or DSGE
models, in Julia.
https://juliacomputing.com/case-studies/ny-fed.html
14

15.  UK cancer researchers turned to Julia to run simulations of tumor growth.
Nature Genetics, 2016
 Approximate Bayesian Computation (ABC) algorithms require potentially millions of
simulations - must be fast
 BioJulia project for analyzing biological data in Julia
 Bayesian MCMC methods Lora.jl and Mamba.jl
https://juliacomputing.com/case-studies/nature.html
15

16.  IBM and Julia Computing analyzed eye fundus images provided by Drishti
Eye Hospitals.
 Timely screening for changes in the retina can help get them to treatment
and prevent vision loss. Julia Computing’s work using deep learning
makes retinal screening an activity that can be performed by a trained
technician using a low cost fundus camera.
https://juliacomputing.com/case-studies/ibm.html
16

17.  Path BioAnalytics is a computational biotech company developing novel
precision medicine assays to support drug discovery and development,
and treatment of disease.
https://juliacomputing.com/case-studies/pathbio.html
17

18.  The Sloan Digital Sky Survey contains nearly 5 million telescopic images of
12 megabytes each – a dataset of 55 terabytes.
 In order to analyze this massive dataset, researchers at UC Berkeley and
Lawrence Berkeley National Laboratory created a new code named
Celeste.
https://juliacomputing.com/case-studies/intel-astro.html
18

19. http://pkg.julialang.org/pulse.html
Julia Package Ecosystem Pulse
19

20. Introduction to Julia
20

21. 一切都從數字開始…
 在Julia中數字有下列幾種形式
 整數
 浮點數
 有理數
 複數
21
Integer
Int8
Int16
Int32
Int64
Int128
Unsigned
Uint8
Uint16
Uint32
Uint64
Uint128
Float
Float16
Float32
Float64

22. 有理數
 有理數表示
 自動約分
 自動調整負號
 接受分母為0
2//3 # 2//3
-6//12 # -1//2
5//-20 # -1//4
5//0 # 1//0
num(2//10) # 1
den(7//14) # 2
2//4 + 1//7 # 9//14
3//10 * 6//9 # 1//5
10//15 == 8//12 # true
float(3//4) # 0.7522

23. 複數
1 + 2im
(1 + 2im) + (3 - 4im) # 4 - 2im
(1 + 2im)*(3 - 4im) # 11 + 2im
(-4 + 3im)^(2 + 1im) # 1.950 + 0.651im
real(1 + 2im) # 1
imag(3 + 4im) # 4
conj(1 + 2im) # 1 - 2im
abs(3 + 4im) # 5.0
angle(3 + 3im)/pi*180 # 45.0
23

24. 變數
 動態型別語言特性
 Value is immutable
x = 5
println(x) # 5
println(typeof(x)) # Int64
x = 6.0
println(x) # 6.0
println(typeof(x)) # Float64
24

25. 算術運算子
 +x： 就是x本身
 -x： 變號
 x + y, x - y, x * y, x / y： 一般四則運算
 div(x, y)： 商
 x % y： 餘數，也可以用rem(x, y)
 x y： 反除，等價於y / x
 x ^ y： 次方
25

26. 位元運算子
 ~x： bitwise not
 x & y： bitwise and
 x | y： bitwise or
 x $ y: bitwise xor
 x >>> y：無正負號，將x的位元右移y個位數
 x >> y：保留正負號，將x的位元右移y個位數
 x << y： 將x的位元左移y個位數
https://www.technologyuk.net/mathematics/number-systems/images/binary_number.gif
26

27. 更新運算子
 +=
 -=
 *=
 /=
 =
 %=
 ^=
 &=
 |=
 $=
 >>>=
 >>=
 <<=
x += 5
等價於
x = x + 5
27

28. 比較運算子
 x == y：等於
 x != y, x ≠ y：不等於
 x < y：小於
 x > y：大於
 x <= y, x ≤ y：小於或等於
 x >= y, x ≥ y：大於或等於
a, b, c = (1, 3, 5)
a < b < c # true
28

29. 不同型別的運算與轉換
 算術運算會自動轉換
 強型別
3.14 * 4 # 12.56
parse(“5”) # 5
convert(AbstractString, 5) # “5”
29

30. If判斷式
 短路邏輯
if <判斷式>
<程式碼>
end
if 3 > 5 && 10 > 0
…
end
30

31. While loop
while <判斷式>
<程式碼>
end
x = …
while <持續條件>
...
x = …
end
31

32. For loop
for i = 1:5 # for迴圈，有限的迴圈次數
println(i)
end
32

33. Array 搭配 for loop
strings = ["foo","bar","baz"]
for s in strings
println(s)
end
33

34. Rand()
 rand(): 隨機0~1
 rand([]): 從裡面選一個出來
y = rand([1, 2, 3])
34

35. Array
 homogenous
 start from 1
 mutable
[ ]2 3 5
A = [2, 3, 5]
A[2] # 3
35

36. 多維陣列
A = [0 -1 1;
1 0 -1;
-1 1 0]
A[1, 2]
36

37. 函式
function add(a, b)
c = a + b
return c
end
37

38. 數值運算
 介紹各種Array函式
zeros(Float64, 2, 2) # 2-by-2 matrix with 0
ones(Float64, 3, 3) # 3-by-3 matrix with 1
trues(2, 2) # 2-by-2 matrix with true
eye(3) # 3-by-3 diagnal matrix
rand(2, 2) # 2-by-2 matrix with random number
38

39. 參數傳遞
 pass-by-sharing
5x
function foo(a)
end
a
39

40. Comprehension
[x for x = 1:3]
[x for x = 1:20 if x % 2 == 0]
["$x * $y = $(x*y)" for x=1:9, y=1:9]
[1, 2, 3]
[2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
[“1 * 1 = 1“, “1 * 2 = 2“, “1 * 3 = 3“ ...]
40

41. Tuple
 Immutable
tup = (1, 2, 3)
tup[1] # 1
tup[1:2] # (1, 2)
(a, b, c) = (1, 2, 3)
41

42. Set
 Mutable
filled = Set([1, 2, 2, 3, 4])
push!(filled, 5)
intersect(filled, other)
union(filled, other)
setdiff(Set([1, 2, 3, 4]), Set([2, 3, 5]))
Set([i for i=1:10])
42

43. Dict
 Mutable
filled = Dict("one"=> 1, "two"=> 2, "three"=> 3)
keys(filled)
values(filled)
Dict(x=> i for (i, x) in enumerate(["one", "two",
"three", "four"]))
43

44. Julia special features
44

45. 支援UTF8符號
 打`alpha<tab>` => α
 α = 1 # 作為變數名稱
 μ = 0
 σ = 1
 normal = Normal(μ, σ)
45

46. Easy to optimize
 Allow generalization and flexibility, and enable to optimize.
 Hints:
 Avoid global variables
 Add type declarations
 Measure performance with @time and pay attention to memory
allocation
 ……
46

47. Easy to profile
 Use @time
 ProfileView.view()
47

48. 增進MATLAB-style的程式效能
 有人在論壇上提到如何增進程式效能，作者發現原本的程式
碼約有50%的時間用在garbage collection，意味著有一半的
時間花在記憶體的分配及釋放
 作者進一步提到，以array-by-array的操作方式是在自
MATLAB背景的人會寫出的程式，若改成element-by-
element的方式就有大幅的改善
 P.S. 在v0.6之後加入了新的功能，不再讓cos(aEll).*gridX .-
sin(aEll).*gridY這樣的運算分配三次記憶體，而是只有一次
http://kristofferc.github.io/post/vectorization_performance_study/
48

49. Easy to parallelize
for i = 1:100000
do_something()
end
@parallel for i = 1:100000
do_something()
end
49

50. Built-in package manager
julia> Pkg.update()
julia> Pkg.add(“Foo”)
julia> Pkg.rm(“Foo”)
50

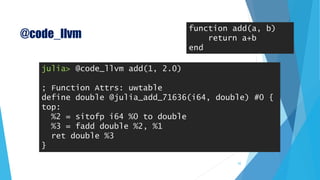
51. @code_native
julia> @code_native add(1, 2)
.text
Filename: REPL[2]
pushq %rbp
movq %rsp, %rbp
Source line: 2
leaq (%rcx,%rdx), %rax
popq %rbp
retq
nopw (%rax,%rax)
function add(a, b)
return a+b
end
51

52. @code_llvm
julia> @code_llvm add(1, 2.0)
; Function Attrs: uwtable
define double @julia_add_71636(i64, double) #0 {
top:
%2 = sitofp i64 %0 to double
%3 = fadd double %2, %1
ret double %3
}
function add(a, b)
return a+b
end
52

53. Julia packages
53

54. 54

55. 55

56. 56

57. 57

58. 58

59. DataFrames.jl
julia> using DataFrames
julia> df = DataFrame(A = 1:4, B = ["M", "F", "F", "M"])
4×2 DataFrames.DataFrame
│ Row │ A │ B │
├─────┼───┼───┤
│ 1 │ 1 │ M │
│ 2 │ 2 │ F │
│ 3 │ 3 │ F │
│ 4 │ 4 │ M │
59

60. DataFrames.jl
julia> df[:A]
4-element NullableArrays.NullableArray{Int64,1}:
1
2
3
4
julia> df[2, :A]
Nullable{Int64}(2)
60

61. DataFrames.jl
julia> df = CSV.read ("data.csv")
julia> df = DataFrame(A = 1:10);
julia> CSV.writetable("output.csv", df)
61

62. DataFrames.jl
julia> names = DataFrame(ID = [1, 2], Name = ["John
Doe", "Jane Doe"])
julia> jobs = DataFrame(ID = [1, 2], Job = ["Lawyer",
"Doctor"])
julia> full = join(names, jobs, on = :ID)
2×3 DataFrames.DataFrame
│ Row │ ID │ Name │ Job │
├─────┼────┼──────────┼────────┤
│ 1 │ 1 │ John Doe │ Lawyer │
│ 2 │ 2 │ Jane Doe │ Doctor │ 62

63. Query.jl
julia> q1 = @from i in dt begin
@where i.age > 40
@select {number_of_children=i.children, i.name}
@collect DataFrame
end
63

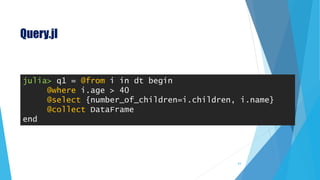
64. StatsBase.jl
 Mean Functions
 mean(x, w)
 geomean(x)
 harmmean(x)
 Scalar Statistics
 var(x, wv[; mean=...])
 std(x, wv[; mean=...])
 mean_and_var(x[, wv][, dim])
 mean_and_std(x[, wv][, dim])
 zscore(X, μ, σ)
 entropy(p)
 crossentropy(p, q)
 kldivergence(p, q)
 percentile(x, p)
 nquantile(x, n)
 quantile(x)
 median(x, w)
 mode(x)
64

65. StatsBase.jl
 Sampling from Population
 sample(a)
 Correlation Analysis of Signals
 autocov(x, lags[; demean=true])
 autocor(x, lags[; demean=true])
 corspearman(x, y)
 corkendall(x, y)
65

66. Distributions.jl
 Continuous Distributions
 Beta(α, β)
 Chisq(ν)
 Exponential(θ)
 Gamma(α, θ)
 LogNormal(μ, σ)
 Normal(μ, σ)
 Uniform(a, b)
 Discrete Distributions
 Bernoulli(p)
 Binomial(n, p)
 DiscreteUniform(a, b)
 Geometric(p)
 Hypergeometric(s, f, n)
 NegativeBinomial(r, p)
 Poisson(λ)
66

67. GLM.jl
67
julia> data = DataFrame(X=[1,2,3], Y=[2,4,7])
3x2 DataFrame
|-------|---|---|
| Row # | X | Y |
| 1 | 1 | 2 |
| 2 | 2 | 4 |
| 3 | 3 | 7 |

68. GLM.jl
68
julia> OLS = glm(@formula(Y ~ X), data, Normal(),
IdentityLink())
DataFrameRegressionModel{GeneralizedLinearModel,Float64
}:
Coefficients:
Estimate Std.Error z value Pr(>|z|)
(Intercept) -0.666667 0.62361 -1.06904 0.2850
X 2.5 0.288675 8.66025 <1e-17

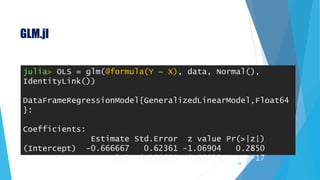
69. GLM.jl
69
julia> newX = DataFrame(X=[2,3,4]);
julia> predict(OLS, newX, :confint)
3×3 Array{Float64,2}:
4.33333 1.33845 7.32821
6.83333 2.09801 11.5687
9.33333 1.40962 17.257
# The columns of the matrix are prediction, 95% lower
and upper confidence bounds

70. Gadfly.jl
70

71. Plots.jl
71
# initialize the attractor
n = 1500
dt = 0.02
σ, ρ, β = 10., 28., 8/3
x, y, z = 1., 1., 1.
# initialize a 3D plot with 1 empty series
plt = path3d(1, xlim=(-25,25), ylim=(-25,25), zlim=(0,50), xlab =
"x", ylab = "y", zlab = "z", title = "Lorenz Attractor", marker = 1)
# build an animated gif, saving every 10th frame
@gif for i=1:n
dx = σ*(y - x) ; x += dt * dx
dy = x*(ρ - z) - y ; y += dt * dy
dz = x*y - β*z ; z += dt * dz
push!(plt, x, y, z)
end every 10

72. Data
 JuliaData
 DataFrames.jl
 CSV.jl
 DataStreams.jl
 CategoricalArrays.jl
 JuliaDB
72

73. File
 JuliaIO
 FileIO.jl
 JSON.jl
 LightXML.jl
 HDF5.jl
 GZip.jl
73

74. Differential equation
 JuliaDiff
 ForwardDiff.jl: Forward Mode Automatic Differentiation for Julia
 ReverseDiff.jl: Reverse Mode Automatic Differentiation for Julia
 TaylorSeries.jl
 JuliaDiffEq
 DifferentialEquations.jl
 Discrete Equations (function maps, discrete stochastic (Gillespie/Markov) simulations)
 Ordinary Differential Equations (ODEs)
 Stochastic Differential Equations (SDEs)
 Algebraic Differential Equations (DAEs)
 Delay Differential Equations (DDEs)
 (Stochastic) Partial Differential Equations ((S)PDEs) 74

75. Probability
 JuliaStats
 JuliaOpt
 JuMP.jl
 Convex.jl
 JuliaML
 LearnBase.jl
 LossFunctions.jl
 ObjectiveFunctions.jl
 PenaltyFunctions.jl
 Klara.jl: MCMC inference in Julia
 Mamba.jl: Markov chain Monte
Carlo (MCMC) for Bayesian
analysis in julia
75

76. Graph / Network
 JuliaGraphs
 LightGraphs.jl
 GraphPlot.jl
76

77. Plot
 Gadfly.jl
 JuliaPlots
 Plots.jl
77

78. Glue
 JuliaPy
 PyCall.jl
 pyjulia
 Conda.jl
 PyPlot.jl
 Pandas.jl
 Seaborn.jl
 SymPy.jl
 JuliaInterop
 RCall.jl
 JavaCall.jl
 CxxWrap.jl
 MATLAB.jl
78

79. Programming
 JuliaCollections
 Iterators.jl
 DataStructures.jl
 SortingAlgorithms.jl
 FunctionalCollections.jl
 Combinatorics.jl
79

80. Web
 JuliaWeb
 Requests.jl
 HttpServer.jl
 WebSockets.jl
 HTTPClient.jl
80

81. 跟其他語言的比較
 Python
 R
 Perl
81

82. Jobs
 Apple, Amazon, Facebook, BlackRock, Ford, Oracle
 Comcast, Massachusetts General Hospital
 Farmers Insurance
 Los Alamos National Laboratory and the National
Renewable Energy Laboratory
82
https://juliacomputing.com/press/2017/01/18/jobs.html

83. Julia Taiwan
 FB社群: https://www.facebook.com/groups/JuliaTaiwan/
 新知發布: https://www.facebook.com/juliannewstw/
83

84. Backup
84

85. 靜態型別與動態型別
 靜態型別跟動態型別最大的差別在於型別是跟著變數還是值。
5
5
x
x
85

86. 強型別與弱型別
5 “5”
5 “5”
+
+
Implicitly
86