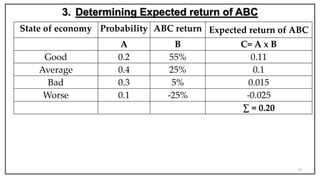
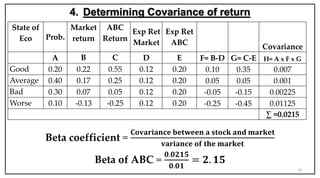
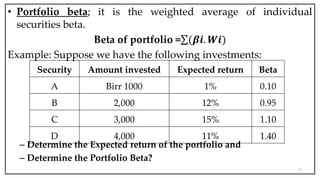
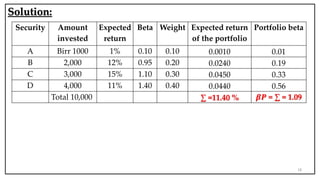
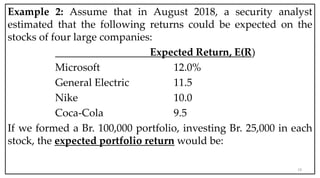
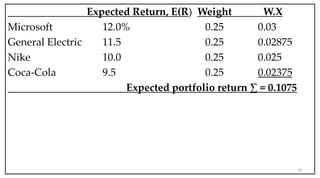
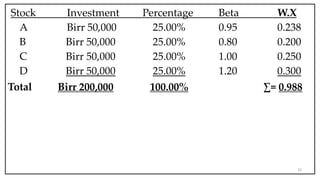
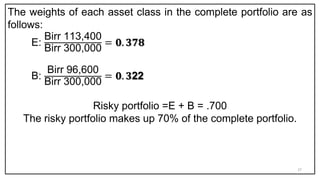
- Portfolio theory deals with constructing portfolios to maximize return for a given level of risk.
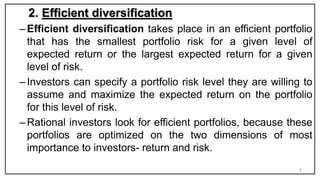
- Diversification reduces unsystematic risk but not all risk. Efficient portfolios provide the lowest risk for a given return.
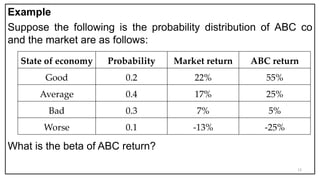
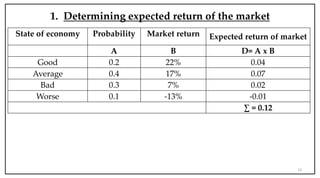
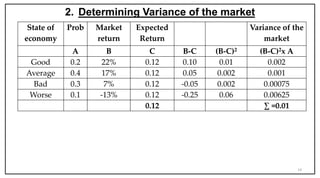
- Beta measures the systematic risk of an asset relative to the market. A beta of 1 means the asset has the same volatility as the market.