Downloaded 50 times
Uploaded byizzulislam_id
Matriks Matematika Wajib
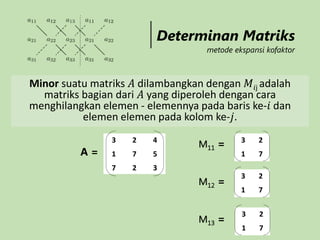
Dokumen ini menjelaskan tentang determinan matriks, termasuk cara menghitungnya untuk matriks ordo 2x2 dan 3x3 menggunakan metode Sarrus dan ekspansi kofaktor. Juga dibahas mengenai invers matriks dan penerapannya dalam menyelesaikan sistem persamaan linear serta kategori solusi yang mungkin muncul. Pengetahuan tentang determinan dan invers sangat penting dalam bidang matematika, terutama dalam aljabar linier.
More Related Content
Similar to Matriks Matematika Wajib
Matriks Matematika Wajib
- 1. MATRIKS Xii PMIIA 8 TUGASMATEMATIKA WAJIB
- 2. penyusun izzul islam noormustain / 14 romadhona lentera putri / 24 sunu pradoto bawono aji / 26
- 3. Determinan Matriks Determinan dinyatakansebagai jumlah semua hasil kali dasar bertanda dari matriks bujur sangkar A. Determinan dari matriks dinotasikan dengan det 𝐴 atau |𝐴|. Nilai dari determinan suatu matriks berupa bilangan real. Determinan dinyatakan sebagai jumlah semua hasil kali dasar bertanda dari matriks bujur sangkar A. Determinan dari sebuah matriks bujur sangkar A, dinotasikan dengan det(A), atau A ORDO 2x2 ORDO 3x3
- 4. Determinan Matriks Jika Amatriks berordo 2x2, misalnya: dc ba A Maka determinan dari matriks A adalah selisih antara perkalian elemen-elemen pada diagonal utama dengan elemen-elemen pada diagonal kedua maka,A dc ba bcadAdet ordo 2x2
- 5. Determinan Matriks Jika Amatriks berordo 3x3, misalnya: Ada dua metode untuk menentukan determinan, yaitu dengan Metode Sarrus dan Metode Ekspansi Kofaktor. ordo 3x3 ihg fed cba A
- 6. Determinan Matriks Jika Amatriks berordo 3x3, misalnya: metode sarrus ihg fed cba A a b c d e f g h i a b s e g h = ptx + quv + rsw – vtr –wup – xsq maka det (B) = Perlu diperhatikan bahwa Metode Sarrus tidak berlaku bila matriks berordo 4x4 dan yang lebih tinggi lagi.
- 7. Determinan Matriks Minor suatumatriks 𝐴 dilambangkan dengan 𝑀𝑖j adalah matriks bagian dari 𝐴 yang diperoleh dengan cara menghilangkan elemen - elemennya pada baris ke-𝑖 dan elemen elemen pada kolom ke-𝑗. metode ekspansi kofaktor 3 2 4 1 7 5 7 2 3 3 2 1 7 3 2 1 7 3 2 1 7 A = M11 = M12 = M13 =
- 8. Determinan Matriks Kofaktor suatuelemen baris ke-𝑖 dan kolom ke-𝑗dari matriks dilambangkan dengan metode ekspansi kofaktor 𝐾𝑖j =(−1)𝑖+𝑗. |𝑀𝑖j| = (−1)𝑖+𝑗.det (𝑀𝑖.j) + - + - + - + - + Penentuan tanda dari determinan matriks persegi berordo 3x3 :
- 9. Invers Matriks Invers matriksadalah lawan atau kebalikan suatu matriks dalam perkalian yang dilambangkan dengan A-1. pengertian Rumus A-1 = invers matriks det A = determinan matriks adj (A) = adjoin matriks det A ≠ 0
- 10. Permasalahan Matriks Penyelesaian SistemPermasalahan Linier dapat ditentukan dengan metode matriks, dengan mengubah bentuk variabel dan koefisien ke dalam bentuk matriks. pengertian 2x + y = 4 3x + 2y = 9 Contoh 2 1 -3 -2 x y 4 9 = Untuk menentukan nilai x dan y, maka bentuk matriks semula diubah menjadi… x y 4 9 = 2 1 -3 -2 -1 menggunakan invers matriks
- 11. Permasalahan Matriks Dalam prosespenyelesaian suatu permasalahan yang ada pada sistem persamaan linier, terdapat beberapa macam solusi yang dapat dijumpai, yaitu : pengertian solusi tunggal solusi banyak tak ada solusi
- 12.