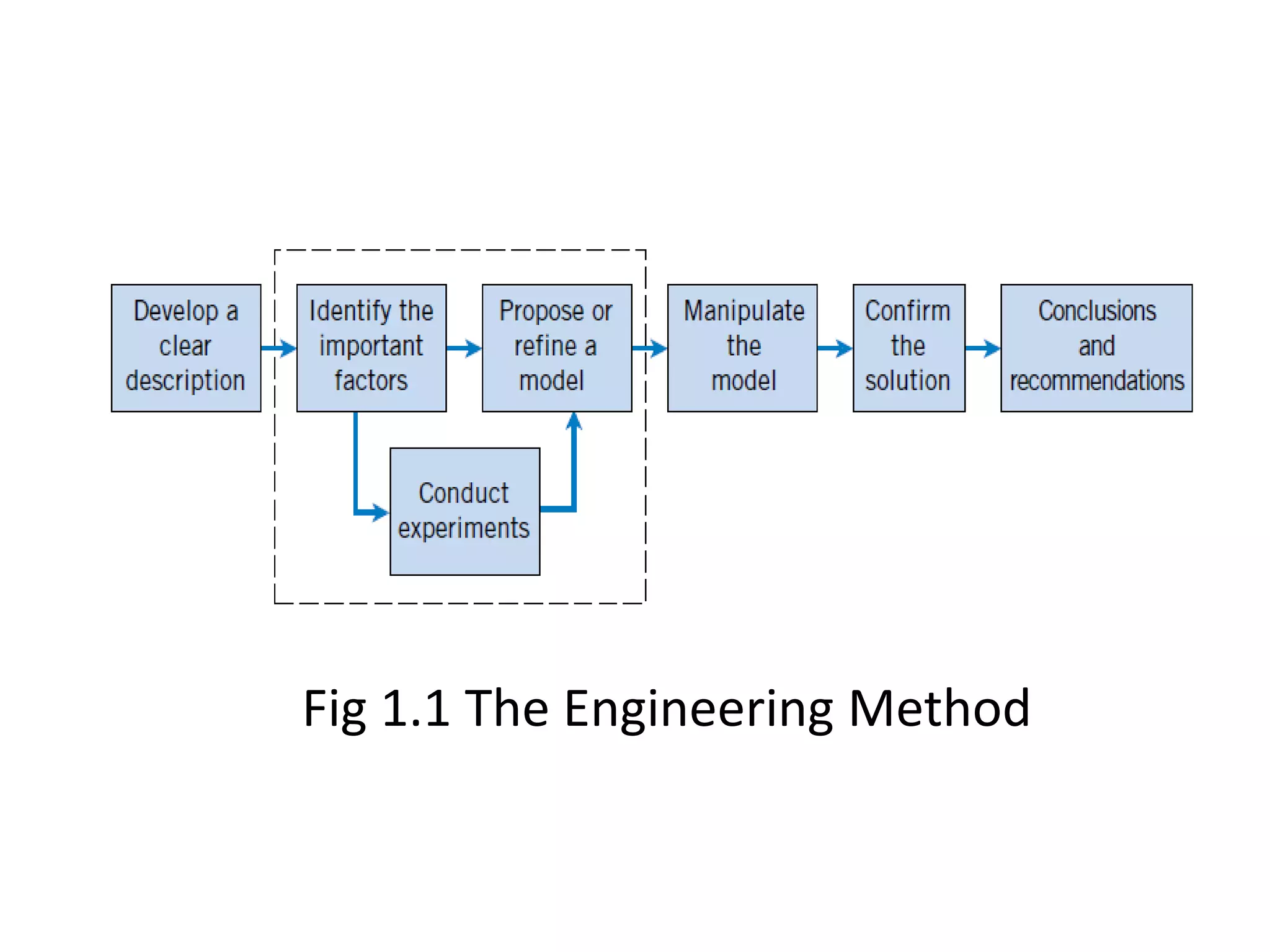
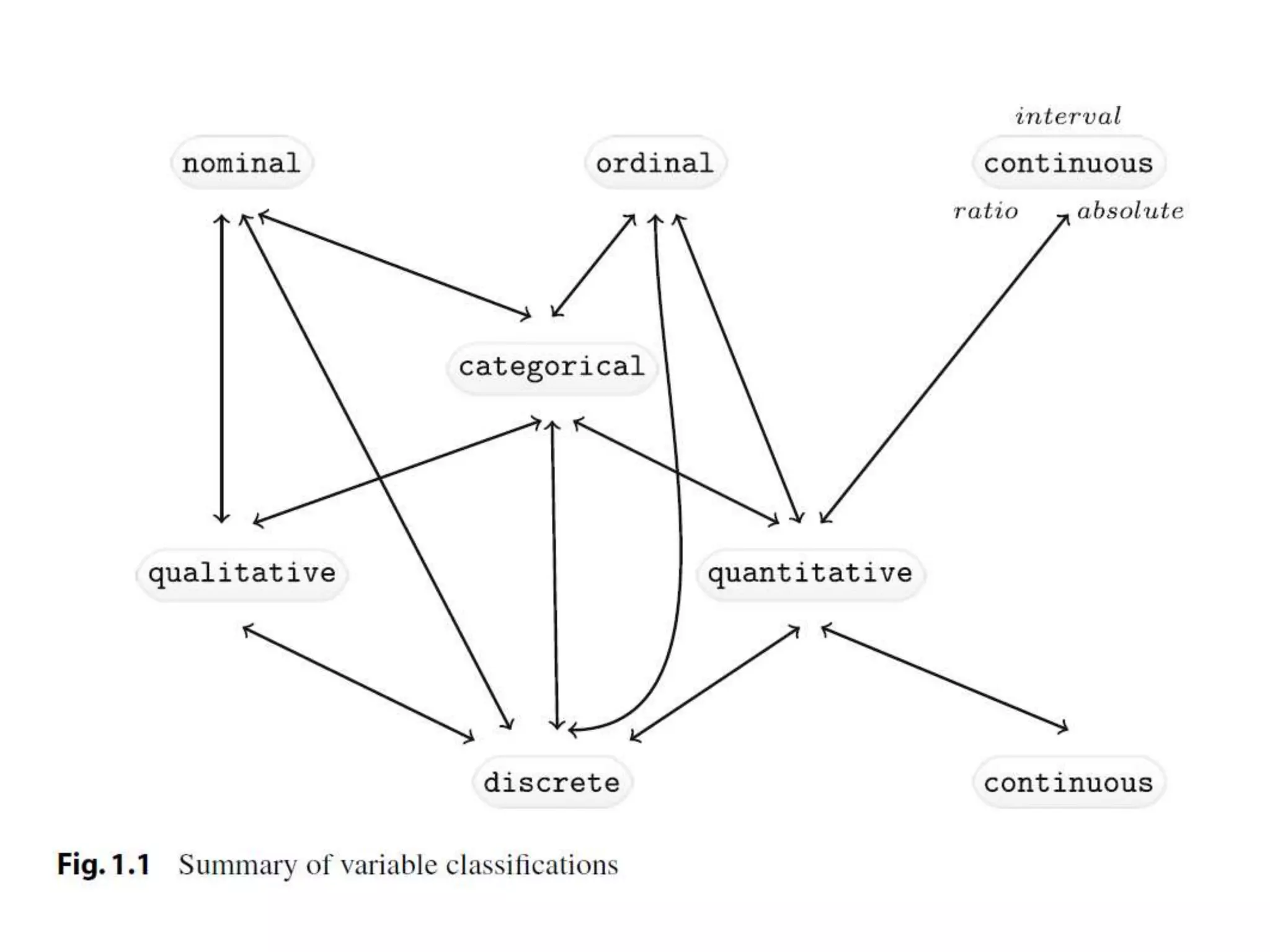
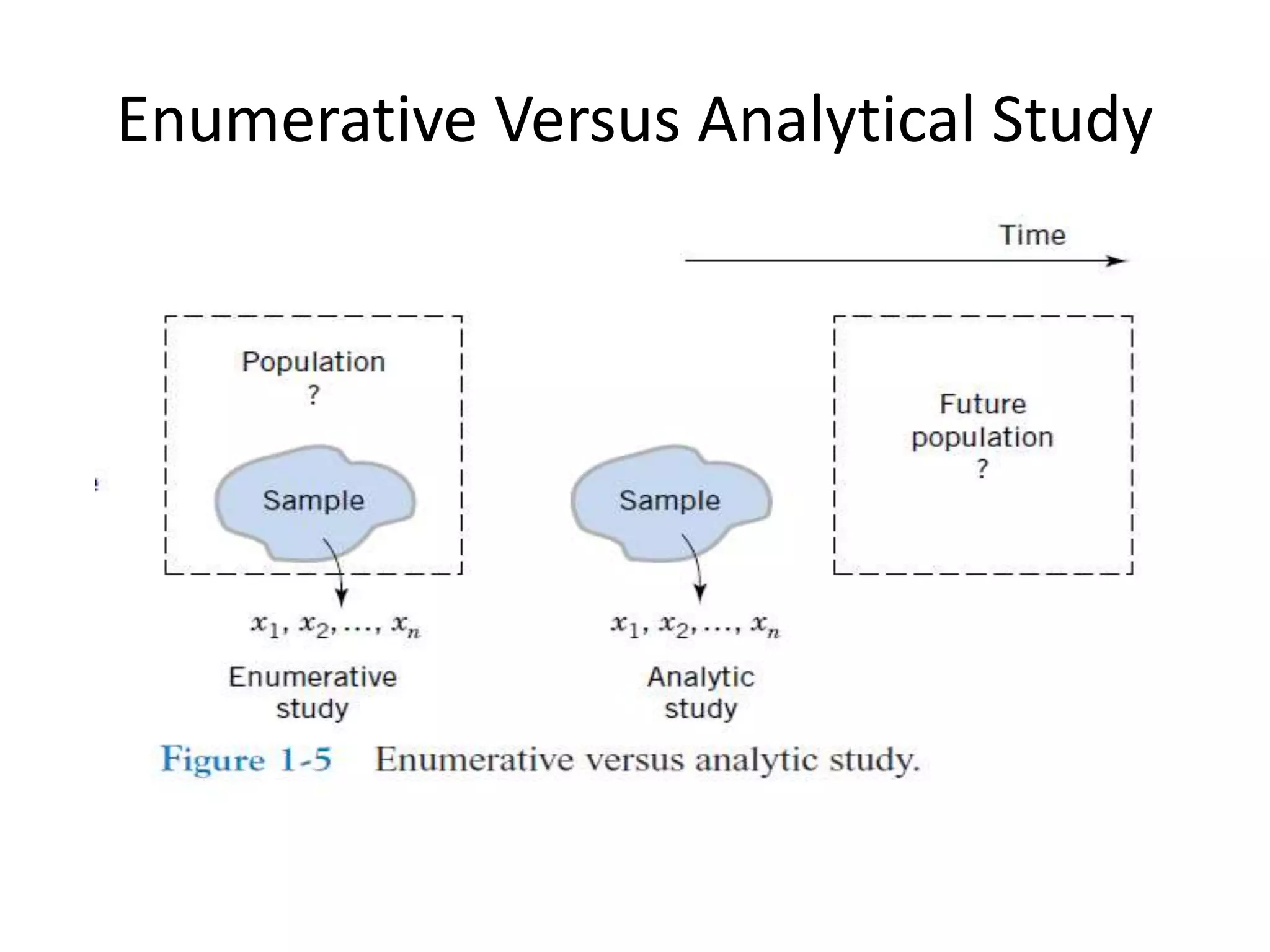
1. The document introduces statistics and probability concepts relevant to engineering problems including collecting and analyzing data. 2. Key methods of collecting engineering data are retrospective studies, observational studies, and designed experiments, with advantages and disadvantages of each. 3. Statistical concepts such as populations, samples, variables, and probability are defined and related to engineering applications.

1. 0CSPC402 Big Data Analytics
Shrihari Khatawkar
sdk_cse@adcet.in
92 26 71 71 93

3. 1. Introduction to Statistics and Probability
• The Engineering method and statistical thinking
• Collecting Engineering data
– Retrospective study
– Observation
– Designed experiments
• Introduction and framework
– Population,
– Sample
– Observations,
– Variables,
– Data collection,
• Sample space and events
– Random Experiments
– Sample Space
– Events
• Interpretation of probability
– Introduction
– Axioms of probability
– Random variables

4. LEARNING OBJECTIVES
• Identify the role that statistics can play in the engineering
problem-solving process
• Discuss how variability affects the data collected and used for
making engineering decisions
• Explain the difference between enumerative and analytical
studies
• Discuss the different methods that engineers use to collect data
• Identify the advantages that designed experiments have in
comparison to other methods of collecting engineering data
• Explain the differences between mechanistic models and
empirical models
• Discuss how probability and probability models are used in
engineering and science

5. Operational Vs Analytics DBs
Operational DBs
• What is current state ?
Store up the last minute
data
• Keep track of the on going
state of process
• SEARCH
Analytical DBs
• Large table collection of
data
• E.g. what change over past
5 years
• More static data set
commutation of data set
overtime or just collection
of stable data
• ANALYSIS uncover new
information

6. The Engineering method and statistical thinking
• Engineers solve problems of interest to society
by the efficient application of scientific
principles
• The engineering or scientific method is the
approach to formulating and solving these
problems.

7. The steps in engineering methods
towards solving problems
1. Develop a clear and concise description of the problem.
2. Identify, at least tentatively, the important factors that affect this problem or that may play a role in
its solution.
3. Propose a model for the problem, using scientific or engineering knowledge of the phenomenon
being studied. State any limitations or assumptions of the model.
4. Conduct appropriate experiments and collect data to test or validate the tentative model or
conclusions made in steps 2 and 3.
5. Refine the model on the basis of the observed data.
6. Manipulate the model to assist in developing a solution to the problem.
7. Conduct an appropriate experiment to confirm that the proposed solution to the problem is both
effective and efficient.
8. Draw conclusions or make recommendations based on the problem solution.

8. Fig 1.1 The Engineering Method

9. The Engineering method and statistical thinking
• The Field of Probability Used to quantify
likelihood or chance Used to represent risk or
uncertainty in engineering applications Can be
interpreted as our degree of belief or relative
frequency
• The Field of Statistics Deals with the
collection, presentation, analysis, and use of
data to make decisions and solve problems,
and design products and processes.

10. The Engineering method and statistical thinking
• The field of statistics deals with the collection,
presentation, analysis, and use of data to
– Make decisions
– Solve problems
– Design products and processes

11. The Engineering method and statistical thinking
• Statistical techniques are useful for describing
and understanding variability.
• By variability, we mean successive
observations of a system or phenomenon do
not produce exactly the same result.
• Statistics gives us a framework for describing
this variability and for learning about potential
sources of variability.
• Example: Mileage performance of Car

12. The Engineering method and statistical thinking
• Engineering Example
Suppose that an engineer is developing a rubber
compound for use in O-rings. The O-rings are
to be employed as seals in plasma etching
tools used in the semiconductor industry, so
their resistance to acids and other corrosive
substances is an important characteristic.

13. The Engineering method and statistical thinking
• Engineering Example
The engineer uses the standard rubber compound
to produce eight O-rings in a development
laboratory and measures the tensile strength of
each specimen after immersion in a nitric acid
solution at 30°C for 25 minutes. The tensile
strengths (in psi) of the eight O-rings are 1030,
1035, 1020, 1049, 1028, 1026, 1019, and 1010.

14. • Engineering Example
The dot diagram is a very useful plot for
displaying a small body of data - say up to
about 20 observations. This plot allows us to
see easily two features of the data; the
location, or the middle, and the scatter or
variability.
The dot diagram is also very useful for
comparing sets of data.

15. Enumerative Versus Analytical Study

16. Collecting Engineering Data
• In the engineering environment, the data are
a sample that has been selected from some
population.
• Three basic methods for collecting data:
– A retrospective study using historical data
– An observational study
– A designed experiment

17. A retrospective study
• It uses either all or a sample of the historical
process data from some period of time.
• In most such studies, the engineers are
interested in using data to construct a model
(called empirical model) relating to the
variables of interest.

18. A retrospective study
–Advantage
• Saves money because the product has already been produced and/or the
data already exists
–Disadvantages
• Data on other factors may be missing.
• Reliability and validity can be questionable.
• The way the data was collected may not be appropriate for the current
study.
• There may be no information recorded to explain anomalies or interesting
observations
• Depending on the amount of time being considered, the data set may be
very large and hard to work with.

19. Anobservationalstudy
• An observational study simply observes the
process of population during a period of routine
operation.
–Advantage•
• With proper planning one can easily obtain
accurate, complete and reliable data.
–Disadvantage
• Does not provide detail information on how
different variables in a process interact to each
other.

20. A designed experiment
• The third way that engineering and scientific data are collected with a
designed experiments.
• In designed experiments, engineers makes deliberate or purposeful
changes in controllable factors of the system, observe the resulting
outputs, and then make decision or inference about which variables are
responsible for the changes that he or she observes in the output
performance.
• Designed Experiments
– Factorial experiment
– Replicates
– Interaction
– Fractional factorial experiment
– One-half fraction

21. Factorial experiment
• In statistics, a full factorial experiment is
an experiment whose design consists of two or more
factors, each with discrete possible values or "levels",
and whose experimental units take on all possible
combinations of these levels across all such factors.
• Replicates are multiple experimental runs with the
same factor settings (levels). Replicates are subject to
the same sources of variability, independently of each
other. ... The design of an experiment includes a step
to determine the number of replicates that you should
run.
Replicates

22. Interaction
• Interactions occur where the impact of a
parameter is dependent on the setting of a
second parameter. Design of experiments can
identify interactions as many parameters are
changed simultaneously in the design. A
commonly seen example of an interaction is time
vs. temperature
• In statistics, fractional factorial designs are
experimental designs consisting of a carefully
chosen subset of the experimental runs of a full
factorial design.
Fractional factorial experiment

23. A designed experiment
–Advantage
• Allows for determination of cause-and-effect
relationships
–Disadvantage
•May not be ethical or possible
•May be expensive

24. Introduction and framework
• Statistics is a collection of methods which help us to describe, summarize,
interpret, and analyze data.
• Drawing conclusions from data is vital in research, administration, and business.
Examples:
• Researchers are interested in understanding whether a medical intervention helps
in reducing the burden of a disease.
• Whether a new fertilizer increases the yield of crops
• How a political system affects trade policy
• Who is going to vote for a political party in the next election
• Identifying people who may be interested in a certain product, optimizing prices,
and evaluating the satisfaction of customers are possible areas of interest.

25. • No matter what the question of interest is, it is
important to collect data in a way which
allows its analysis.
• The representation of collected data in a data
set or data matrix allows the application of a
variety of statistical methods.

26. Introduction of terminology
Population, Sample, and Observations
• The units on which we measure data—such as persons,
cars, animals, or plants—are called observations.
• These units/observations are represented by the
Greek symbol ω. The collection of all units is called
population and is represented by Ω.
• When we refer to ω ϵ Ω , we mean a single unit out of
all units, e.g. one person out of all persons of interest.
• If we consider a selection of observations ω1, ω2,…. ωn ,
then these observations are called sample. A sample is
always a subset of the population, {ω1, ω2,…. ωn} ⊆ Ω.

27. Example
• If we are interested in the social conditions
under which Indian people live, then we
would define all inhabitants (population) of
India as Ω and each of its inhabitants as ω. If
we want to collect data from a few
inhabitants, then those would represent a
sample from the total population.

28. Population
• population refers to the total set of observations
that can be made.
Example
• If we are studying the weight of adult women, the
population is the set of weights of all the women in
the world.
• A sample is a set of data collected and/or
selected from a population by a defined
procedure.

29. Variables
• If we have specified the population of interest
for a specific research question, we can think
of what is of interest about our observations.
• A particular feature of these observations can
be collected in a statistical variable X.
• Any information we are interested in may be
captured in such a variable.

30. • Example, if our observations refer to human
beings, X may describe marital status, gender,
age, or anything else which may relate to a
person.
• Of course, we can be interested in many
different features, each of them collected in a
different variable Xi, i = 1,2,...,p. Each
observation ω takes a particular value for X.
• If X refers to gender, each observation, i.e.
each person, has a particular value x which
refers to either “male” or “female”.

31. • The formal definition of a variable is
X : Ω → S
ω → x
• This dentition states that a variable X takes a
value x for each observation ω ∈ Ω, whereby
the number of possible values is contained in
the set S.

32. • A variable is any characteristics, number,
or quantity that can be measured or counted. A
variable may also be called a data item. Age, sex,
business income and expenses, country of birth,
capital expenditure, class grades, eye colour and
vehicle type are examples of variables. It is called
a variable because the value may vary between
data units (Obsevation) in a population, and may
change in value over time.

33. Variables
• Qualitative and Quantitative Variables
• Discrete and Continuous Variables
• Scales
• Grouped Data

34. Qualitative variables
• Qualitative variables are the variables which
take values x that cannot be ordered in a
logical or natural way.
Example
• The color of the eye,
• The name of a political party,
• The type of transport used to travel to work

35. Quantitative variables
• Quantitative variables represent measurable
quantities. The values which these variables can
take can be ordered in a logical and natural way.
Examples
• Size of shoes,
• Price for houses,
• Number of semesters studied,
• Weight of a person

36. variable “gender” ?
• It is common to assign numbers to qualitative variables for
practical purposes in data analyses.
• For instance, if we consider the variable “gender”, then
each observation can take either the “value” male or
female.
• We may decide to assign 1 to female and 0 to male and use
these numbers instead of the original categories. However,
this is arbitrary, and we could have also chosen “1” for male
and “0” for female, or “2” for male and “10” for female.
• There is no logical and natural order on how to arrange
male and female, and thus, the variable gender remains a
qualitative variable, even after using numbers for coding
the values that X can take.

37. DISCRETE AND CONTINUOUS
VARIABLES

38. Discrete Variables
• Discrete variables are variables which can
only take a finite number of values.
• All qualitative variables are discrete, such as
the colour of the eye or the region of a
country. But also quantitative variables can be
discrete: the size of shoes or the number of
semesters studied would be discrete because
the number of values these variables can take
is limited.

39. Continuous Variables
• Variables which can take an infinite number of
values are called continuous variables.
• Sometimes, it is said that continuous
variables are variables which are “measured
rather than counted”.
• Examples

40. Examples
• Time it takes to travel to university, the distance
between two planets.
• The crucial point is that continuous variables can, in
theory, take an infinite number of values
• For instance, the height of a person may be recorded
as 172 cm. However, the actual height on the
measuring tape might be 172.3 cm which was rounded
off to 172 cm. If one had a better measuring
instrument, we may have obtained 172.342 cm. But
the real height of this person is a number with
indefinitely many decimal places such as
172.342975328…..cm.
• No matter what we eventually report or obtain, a
variable which can take an infinite amount of values is
defined to be a continuous variable

41. Scales
• Different variables contain different amounts of
information. A useful classification of these
considerations is given by the concept of the
scale of a variable.
• Nominal scale
• Ordinal scale
• Continuous scale.
– Interval scale
– Ratio scale
– Absolute scale.

42. Nominal scale
• The values of a nominal variable cannot be
ordered.
• Examples are the gender of a person (male–
female) or the status of an application
(pending–not pending).

43. Ordinal scale
• The values of an ordinal variable can be ordered. However, the
differences between these values cannot be interpreted in a
meaningful way.
Example,
• The possible values of education level (none–primary education–
secondary education–university degree) can be ordered
meaningfully, but the differences between the values cannot be
interpreted.
• Likewise, the satisfaction with a product
• (unsatisfied – satisfied – very satisfied) is an ordinal variable
because the values this variable can take can be ordered, but the
differences between “unsatisfied– satisfied” and “satisfied–very
satisfied” cannot be compared in a numerical way.

44. Continuous scale
• The values of a continuous variable can be
ordered. Furthermore, the differences between
these values can be interpreted in a meaningful
way.
Example
• the height of a person refers to a continuous
variable because the values can be ordered (170
cm, 171 cm, 172 cm, …), and differences between
these values can be compared (the difference
between 170 and 171 cm is the same as the
difference between 171 and 172 cm).

45. • Continuous scale is divided further into
subscales
– Interval scale
– Ratio scale
– Absolute scale.

46. • Interval scale : Only differences between values, but not
ratios, can be interpreted.
An example : Temperature (measured in ◦C): the difference
between −2 ◦C and 4 ◦C is 6◦C, but the ratio of 4/−2 =−2 does
not mean that −4 ◦C is twice as cold as 2 ◦C.
• Ratio scale. Both differences and ratios can be interpreted.
An example is speed: 60 km/h is 40 km/h more than 20 km/h.
Moreover, 60 km/h is three times faster than 20 km/h
because the ratio between them is 3.
• Absolute scale. The absolute scale is the same as the ratio
scale, with the exception that the values are measured in
“natural” units.
An example is “number of semesters studied” where no artificial
unit such as km/h or◦C is needed: the values are simply
1,2,3,... .

47. Grouped Data
• Data may be available only in a summarized form:
instead of the original value, one may only know
the category or group the value belongs to.
Example,
• Income (per year) by means of groups:
– [(<Rs–20,000), [Rs 20,000–RS 30,000),...,>Rs 100,000];
• If there are many political parties in an election,
those with a low number of voters are often
summarized in a new category “Other Parties”;

48. • If data is available in grouped form, we call the
respective variable capturing this information a
grouped variable. Sometimes, these variables are
also known as categorical variables
• It refer to any type of variable which takes a
finite, possibly small, number of values.
• Any discrete and/or nominal and/or ordinal
and/or qualitative variable may be regarded as a
categorical variable.
• Any grouped or categorical variable which can
only take two values is called a binary variable.

49. • Qualitative data is always discrete, but
quantitative data can be both discrete (e.g. size of
shoes or a grouped variable) and continuous (e.g.
temperature).
• Nominal variables are always qualitative and
discrete (e.g. colour of the eye), whereas
continuous variables are always quantitative (e.g.
temperature).
• Categorical variables can be both qualitative (e.g.
colour of the eye) and quantitative (satisfaction
level on a scale from 1 to 5). Categorical variables
are never continuous.

51. What is Data Set ?

52. Data Collection
• Survey. A survey typically (but not always)
collects data by asking questions (in person or
by phone) or providing questionnaires to
study participants (as a printout or online).

53. Experiment
Experimental data is obtained in “controlled”
settings. This can mean many things, but
essentially it is data which is generated by the
researcher with full control over one or many
variables of interest.
Example:
• Two competing toothpastes

54. Observational Data
• Observational data is data which is collected
routinely, without a researcher designing a
survey or conducting an experiment
Example
• Suppose a government institution monitors
where people live and move to. This data can
later be used to explore migration patterns.

55. Primary and Secondary Data :
• Primary data is data we collect ourselves,
• Example:
– a survey or experiment.
• Secondary data, in contrast, is collected by someone else.
Example:
– Data from a national census,
– Publicly available databases,
– Previous research studies,
– Government reports,
– Historical data,
– Data from the internet

56. • Data is usually stored in a data matrix where
the rows represent the observations and the
columns are variables. It can be analyzed with
statistical software.

57. Sample Space and events
– Random Experiments
– Sample Space
– Events

58. Random Experiment
• Result is not predictale but know the possibel
outcome
• Ex.
– Flipping a coin : Head or tails
– Die: 1,2,3,4,5,6,
– Playing Cards : 1 to 52

59. What are the possible outcomes ?

60. Sample Space
Sample Space and Sample Point
Sample Point

61. What is probability of getting < 3 in
one throw of die
Events

62. Basic Concepts of Probability
• What is a sample space ?
– All Possible Outcomes
• What is a sample point ?
– One Possible outcome
(any one outcome from all possible outcomes )
• What is a event ?
– One or more from possible outcomes

63. Sample Space
• For tossing a single coin {H,T}
• For tossing a two coins {HH, HT, TT, TH}
• For two die - ?
• Coin and Die – Tail steady, head  die

64. Examples
• Given a standard die, determine the
probability for the following events when
rolling the die one time:
1. P(5)
2. P(even number)
3. P(7)

65. Solution

68. What Is A Random Variable?
• We often come across the terms “measurable” or
“observable” when reading financial papers. The
term observable represents a random variable in
an experiment that can be measured.
• A random variable itself is a function. It maps a
state space to a set of numbers, hence a random
variable is an outcome that is random in nature.
Each outcome has a probability associated with
it.

69. Example:
• GDP of a country is a random variable. It can be
considered as a function of many variables and
constants. Each event has a probability measure
associated with it.
• Throwing a dice,
• Flipping a coin,
• Days of a week,
• The interest rates,
• Price of gold, etc.
• A random variable can be discrete or
continuous.

70. Discrete Random Variable
• A discrete random variable is one that has a finite set
of possible outcomes.
• These outcomes can also be countably infinite but the
key to note is that the sum of the finite set of
outcomes should be 1.
Example:
– Throwing a dice,
– Flipping a coin,
– Days of a week,
– Colours in a particular pencil box,
– Gender, months,
– days of a month, etc.

71. Continuous Random Variable
• A random variable that is not discrete is a
continuous random variable. It has an infinite set
of possible outcomes that cannot be counted.
Example:
– The population of the world that is dependent on
time,
– the interest rates,
– exchange rates,
– price of gold,
– rainfall in millimeters, etc.

72. Summary
• The random number is a function of outcomes
where each outcome is random and has a
probability associated with it.

73. INTERPRETATION OF
PROBABILITY
INTRODUCTION
AXIOMS OF PROBABILITY
RANDOM VARIABLES

74. Axioms of probability
• Axioms meaning
– accepted truth or
– a statement or proposition on which an
abstractly defined structure is based.

75. • The axioms ensure that the probabilities
assigned in an experiment can be interpreted
as relative frequencies and that the
assignments are consistent with our intuitive
understanding of relationships between
relative frequencies.
Example,
• If event A is contained in event B, we should
have

76. Axioms of probability

78. • A random experiment can result in one of the
outcomes {a, b, c, d} with probabilities 0.1, 0.3, 0.5,
and 0.1, respectively. Let A denote the event {a, b}, B
the event {b, c, d}, and C the event {d}.Then,
– P1(A) = ?
– P1 (B) =?
– P1 (C) = ?
– P(A’), P(B’), P(C’) = ?
– P1 (A ⋂ B) =?
– P(A ⋃ B) =?
– P (A ⋂ C) = ?

79. • A= {a, b},
• B= {b, c, d},
• C= {d}.
– P1(A) = 0.1 + 0.3 = 0.4
– P1 (B) = 0.3 + 0.5 + 0.1 = 0.9
– P1 (C2) = 0.1
– P(A’), = 0.6 P(B’) = 0.1, P(C’) = 0.9
– P1 (A ⋂ B) = 0.3
– P(A ⋃ B) = 1
– P (A ⋂ C) = 0

80. Try