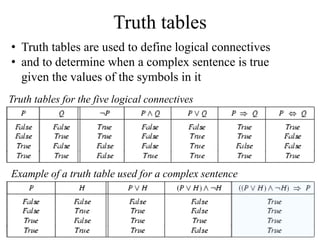
Propositional logic and predicate logic are knowledge representation languages used in AI. Propositional logic uses symbols to represent simple statements, while predicate logic (first-order logic) is more expressive and commonly used, using predicates, quantifiers and variables to represent relationships about objects in the world. Some key aspects of first-order logic include its syntax, semantics, how it can represent statements about universality and existence using quantifiers, and how it can be used to formally represent real-world knowledge and relationships.

1. Propositional Logic and
predicate logic

2. Big Ideas
• Logic is a great knowledge representation
language for many AI problems
• Propositional logic is the simple
foundation and fine for some AI problems
• First order logic (FOL) is much more
expressive as a KR language and more
commonly used in AI
• There are many variations: horn logic,
higher order logic, three-valued logic,
probabilistic logics, etc.

3. Propositional logic (PL)
• Simple language for showing key ideas and definitions
• User defines set of propositional symbols, like P and Q
• User defines semantics of each propositional symbol:
– P means “It is hot”, Q means “It is humid”, etc.
• A sentence (well formed formula) is defined as
follows:
– A symbol is a sentence
– If S is a sentence, then S is a sentence
– If S is a sentence, then (S) is a sentence
– If S and T are sentences, then (S  T), (S  T), (S  T), and (S
↔ T) are sentences
– A sentence results from a finite number of applications of the
rules

4. Propositional logic
• Logical constants: true, false
• Propositional symbols: P, Q,... (atomic sentences)
• Wrapping parentheses: ( … )
• Sentences are combined by connectives:
 and [conjunction]
 or [disjunction]
implies [implication / conditional]
 is equivalent[biconditional]
 not [negation]
• Literal: atomic sentence or negated atomic sentence
P,  P

5. Examples of PL sentences
• (P  Q)  R
“If it is hot and humid, then it is raining”
• Q  P
“If it is humid, then it is hot”
• Q
“It is humid.”
• We’re free to choose better symbols, btw:
Ho = “It is hot”
Hu = “It is humid”
R = “It is raining”

6. Some terms
• The meaning or semantics of a sentence
determines its interpretation
• Given the truth values of all symbols in a
sentence, it can be “evaluated” to determine
its truth value (True or False)
• A model for a KB is a possible world – an
assignment of truth values to propositional
symbols that makes each sentence in the KB
True

7. Truth tables
Truth tables for the five logical connectives
Example of a truth table used for a complex sentence
• Truth tables are used to define logical connectives
• and to determine when a complex sentence is true
given the values of the symbols in it

8. On the implies connective:
P  Q
• Note that  is a logical connective
• So PQ is a logical sentence and has a
truth value, i.e., is either true or false
• If we add this sentence to the KB, it can be
used by an inference rule, Modes Ponens, to
derive/infer/prove Q if P is also in the KB
• Given a KB where P=True and Q=True, we
can also derive/infer/prove that PQ is
True

9. Propositional Logic can’t say
• If X is married to Y, then Y is married to X.
• If X is west of Y, and Y is west of Z, then X
is west of Z.
• And a million other simple things.
• Fix:
– extend representation: add predicates
– Extend operator(resolution): add unification

10. Syntax
• See text for formal rules.
• All of propositional + quantifiers, predicates,
functions, and constants.
• Variables can take on values of constants or terms.
• Term = reference to object
• Variables not allowed to be predicates.
– E.G. What is the relationship between Bill and Hillary?
• Text Notation: variables lower case, constants upper
• Prolog Notation: variables are upper case, etc

11. Semantics
• Validity = true in every model and every
interpretation.
• Interpretation = mapping of constants,
predicates, functions into objects, relations,
and functions.

12. Advance Artificial
Intelligence
12
Predicate Calculus
So it is a better idea to use predicates instead of
propositions.
This leads us to predicate calculus.
Predicate calculus has symbols called
• object constants,
• relation constants, and
• function constants
These symbols will be used to refer to objects in the world
and to propositions about the word.

13. Advance Artificial
Intelligence
13
Quantification
Introducing the universal quantifier  and the existential
quantifier  facilitates the translation of world knowledge
into predicate calculus.
Examples:
Paul beats up all professors who fail him.
x(Professor(x)  Fails(x, Paul)  BeatsUp(Paul, x))
There is at least one intelligent UMB professor.
x(UMBProf(x)  Intelligent(x))

14. Representing World in FOL
• All kings are persons.
 goes to?
• for all x, King(x) & Person(x).
• for all x, King(x) => Person(x).

15. Representing World in FOL
• All kings are persons.
• for all x, King(x) => Person(x). OK.
• for all x, King(x) & Person(x). Not OK.
– this says every object is a king and a person.
• In Prolog: person(X) :- king(X).
• Everyone Likes icecream.
• for all x, Likes(x, icecream).

16. Negating Quantifiers
• ~ there exist x, P(x)
• ~ for all x, P(x)
For all x, Likes(x,Icecream)
No one likes liver.
For all x, not Likes(x,Liver)
• For all x, ~P(x)
• There exists x, ~P(x)
• There does not exist an x,
not Likes(x,Icecream)
• Not there exists x,
Iikes(x,Liver).

17. More Translations
• Everyone loves
someone.
• There is someone that
everyone loves.
• Everyone loves their
father.
• See text.
• For all x, there is a y(x)
such that Loves(x,y(x)).
• There is an M such that
for all x, Loves(x,M).
• M is skolem constant
• For all x,
Loves(x,Father(x)).
• Father(x) is skolem
function.

18. Occurs Checking
• When unifying a variable against a complex
term, the complex term should not contain
the same variable, else non-match.
• Prolog doesn’t check this.
• Ex. f(X,X) and f(Y,g(Y)) should not unify.

19. Modeling with Definite Clauses:
at most one positive literal
1. It is a crime for an american to sell weapons to a
hostile country.
1’. American(x)&Weapons(y)&Hostile(z) &
Sell(x,y,z) => Criminal (x).
2. The country Nono has some missiles.
There exists x Owns(Nono,x)&Missile(x).
2’. Missile(M1). … Skolem Constant introduction
2’’. Owns(Nono,M1).

20. Resolution gives forward chaining
• Enemy(x,America)
=>Hostile(x)
• Enemy(Nono,America)
• |- Hostile(Nono)
• Not Enemy(x,America)
or Hostile(x)
• Enemy(Nono,America)
• Resolve by {x/Nono}
• To Hostile(Nono)

21. FOL -> Conjuctive Normal Form
• Similar to process for propositional logic, but
• Use negations rules for quantifiers
• Standarize variables apart
• Universal quantification is implicit.
• Skolemization: introduction of constants and
functions to remove existential quantifiers.

22. Time
• Before (x,y) implies After(y,x)
• After(x,y) imples Before(y,x)
• Before(x,y) and Before(y,z) implies
Before(x,z) etc.
• When are you done?
• What about during?

23. Space and more
• In(x,y) and In(y,z) implies in(x,z).
• Infront, behind, etc
• Frame problem: you turn, some predicates
change and some don’t.
• etc.
And lots more: heat, wind, hitting, physical
objects versus thoughts, knowing,