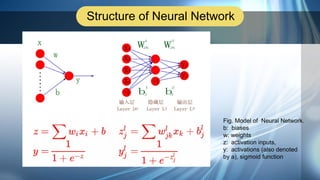
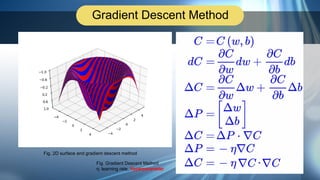
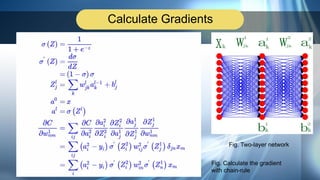
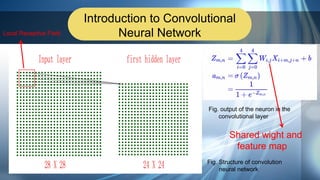
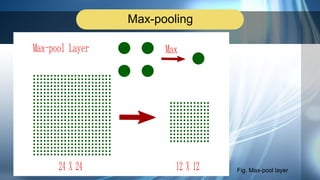
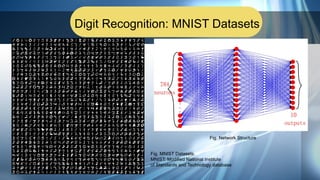
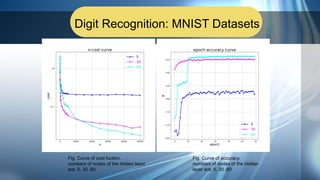
1. The document introduces neural networks and the backpropagation algorithm. It discusses the structure of neural networks and how they are trained on data to learn parameters through methods like gradient descent. 2. Backpropagation is introduced as an efficient method to calculate gradients in neural networks using chain rule. Diagrams show the calculations and flow of backpropagation. 3. Applications of neural networks like convolutional neural networks and digit recognition using the MNIST dataset are demonstrated. AlexNet, an early CNN model for image recognition, is discussed.

1. Speaker: Deping Huang
09/29/2017

2. 1
2
3
Introduction to Neural Network and
Backpropagation algorithm
Dealing with MNIST datasets
and digit recognition
Brief History of Artififcal Intelligence
and Introduction to Machine Learning
A Simple Example
Models and Methods
Research Background
Outline

3. Research Background
Fig. AlphaGo VS Lee Sedol Fig. AlphaGo VS Ke Jie

4. Research Background
Fig. Professor Feifei Li Fig. Datasets of IMAGENET.
14,197,122 images, 21841 synsets indexed

5. Research Background
Fig. Images that combine
the content of a photograph
with the style of several well-
known artworks
2014, ArXiv, A Neural Algorithm of Artistic Style

6. Machine Learning
supervised learning unsupervised learning
Reinforcement learning

7. Some Machine Learning Methods
Support Vector Machine Neural NetworkRestricted Bolzman
Machine

8. What is Neural Network?
Fig. What is Neural
Network?

9. Structure of Neural Network
Fig. Model of Neural Network.
b: biases
w: weights
z: activation inputs,
y: activations (also denoted
by a), sigmoid function

10. Training: From Data
to Parameters
,"bird"
,"bird"
,"bird"
,"cat"
,"cat"
,"cat"
,"dog"
,"dog"
,"dog"
N
e
t
w
o
r
k
"bird"Neural networks get parameters from huge amouts
of data, it is called training!

11. Cost Function
Fig. Cost function
Why 1/2 ?
"cat"
y =a, c=0
y!=a, c=2
1/2 is a normalized factor
"bird"
"dog"

12. Gradient Descent Method
Fig. Gradient Descent Method
η: learning rate, Hyperparameter
Fig. 2D surface and gradient descent method

13. Stochastic Gradient Descent
Method
Fig. Stochastic Gradient Descent
Methods
Generally, m is far smaller than n.
Using stochastic gradient descent
method, we can get results much
faster with a little loss of accuracy
We shuffle the data
and split it to many
pieces with size m.

14. Calculate Gradients
Fig. Calculate the gradient
with chain-rule
Fig. Two-layer network

15. Fig. Calculate the gradients with
the definition of partial deriviate
It is too complicated using chain-rule
to calculate gradients!
We should calculate the cost for
every parameter which is too
time-costed!
Calculate Gradients

16. Backpropagation Algorithm
Fig. Four Formulas of BP algorithm.
δ: errors of each layer
Hadamard Product
errors of each layer
2016, Michael Nielsen, Introduction to Neural Networks and Deep Learning

17. Backpropagation Algorithm
Fig. Prove of the formulas of
backpropagation algorithm.
It is the application of chain-rule in
calculas
BP1
BP4
BP3
BP2

18. Algorithm Flowchart
Fig. Algorithm flowchart of the
training of neural networks
1. we should design the network topology.
How many neurons each layer ?
How many layers?
2. Data(include input and output) should
be given.
3. update the parameters with SGD
algorithm.

19. Introduction to Convolutional
Neural Network
Fig. Structure of convolution
neural network
Local Receptive Field

20. Introduction to Convolutional
Neural Network
Fig. Structure of convolution
neural network
Local Receptive Field
Fig. output of the neuron in the
convolutional layer
Shared wight and
feature map

21. Max-pooling
Fig. Max-pool layer

22. Application of CNN
Fig. Structure of AlexNet
Datasets: 1.2 million
images with the size of
224x224;
150,000 images used for
testing
2012, Alex Krizhevsky,*
Over 60 million parameters
Accuracy: 84.7%

23. Digit Recognition: MNIST Datasets
Fig. MNIST Datasets.
MNIST: Modified National Institute
of Standards and Technology database
Fig. Network Structure

24. Digit Recognition: MNIST Datasets
Fig. Curve of accuracy.
numbers of nodes of the hidden
layer are: 5, 30 ,60
Fig. Curve of cost fuction.
numbers of nodes of the hidden layer
are: 5, 30 ,60

25. Conclutions
1. We introduce the training method of
neural network: BP algorithm
2. We introduce Convolutional Neural
Network.
3. Some simple results about digit
recogntion.

26. Then.....
What Can We Do With
Neural Network?

27. THANKS