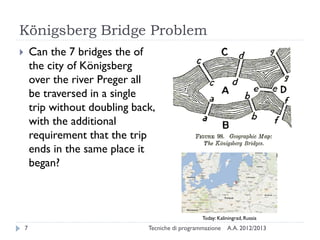
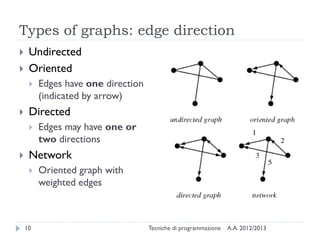
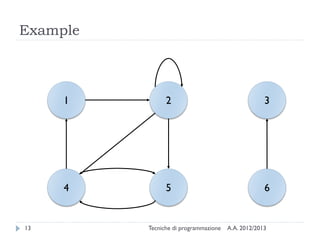
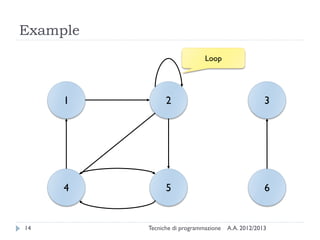
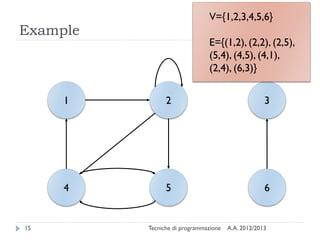
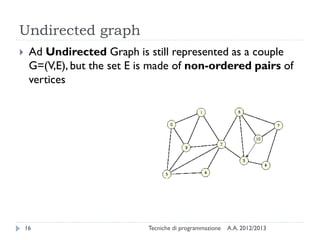
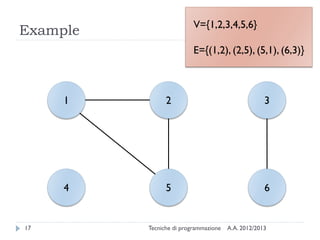
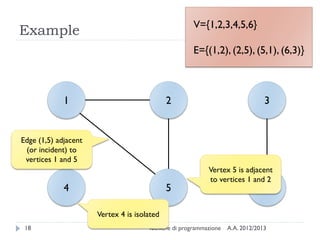
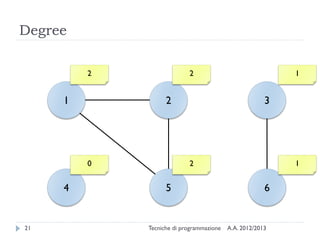
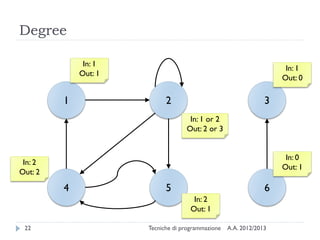
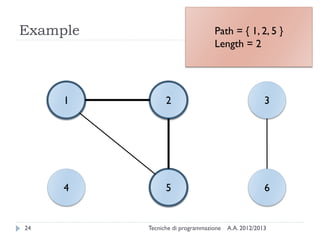
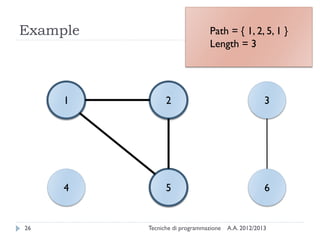
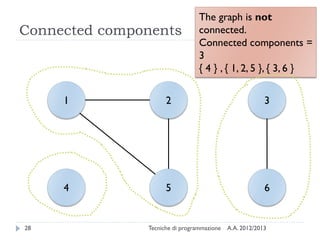
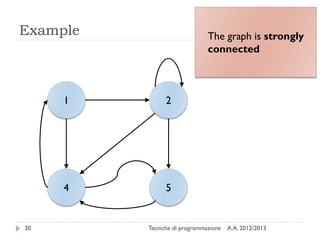
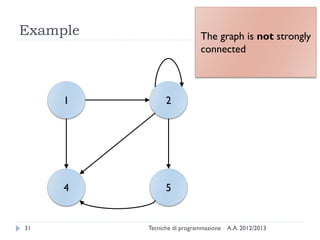
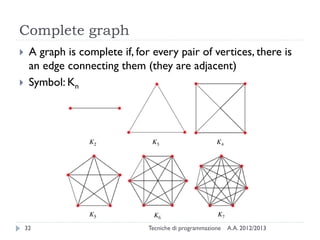
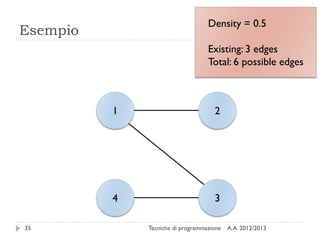
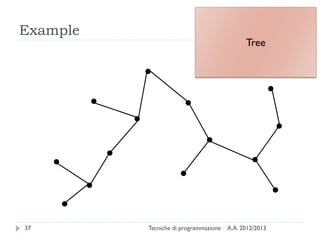
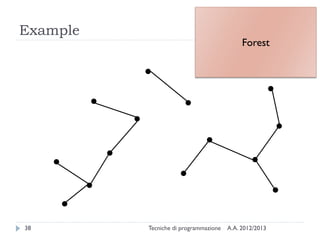
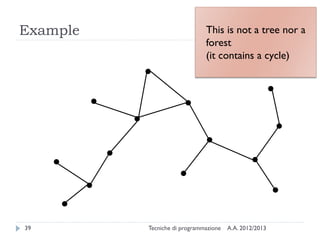
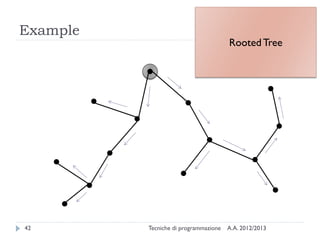
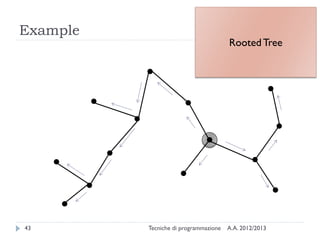
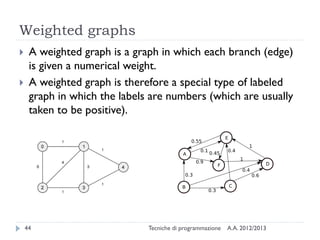
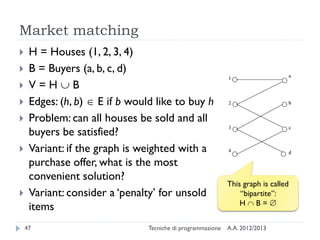
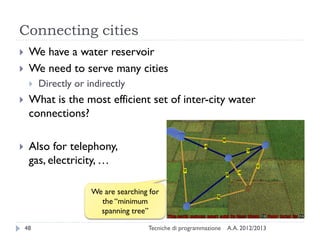
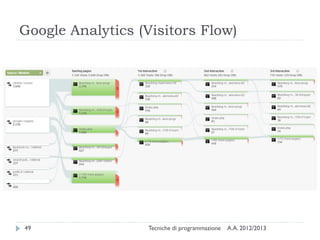
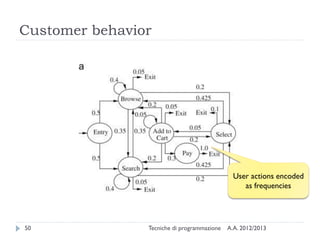
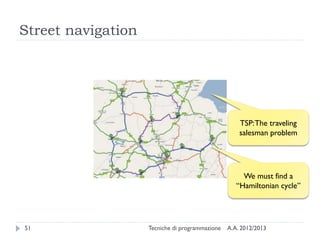
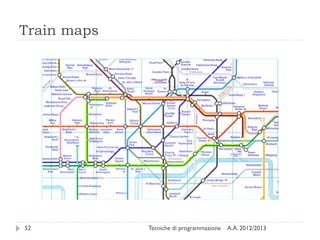
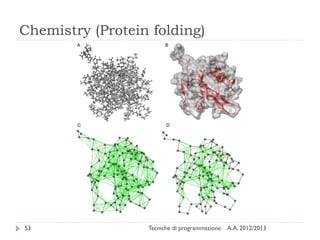
The document is an introduction to graph theory, defining graphs as collections of points and lines connecting them, with various types including simple graphs, multigraphs, and directed graphs. It discusses key concepts such as paths, cycles, connectivity, and applications in real-world problems like navigation and social networks. The document also covers historical context, graph properties, and concludes with resources for further information.