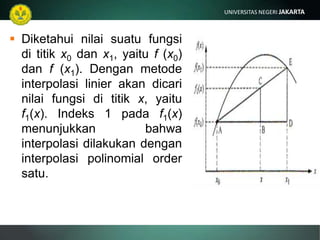
Dokumen ini membahas tentang interpolasi polinomial. Metode interpolasi linier digunakan untuk menghubungkan dua titik data dengan garis lurus. Interpolasi Lagrange menggunakan persamaan polinomial untuk menghubungkan beberapa titik data. Interpolasi polinomial dapat digunakan untuk memodelkan data pengukuran dengan persamaan polinomial.

1. Sesions#11Interpolasi PolinomialBambangHeruIswantoDr.rer.natM.SiJurusanFisikaFakultasMatematikadanIlmuPengetahuanAlam

2. Outline Interpolasi LinierInterpolasi LagrangeInterpolasi Polinomil dari data pengukuran

3. Interpolasi LinierBentuk paling sederhana dari interpolasi adalah menghubungkan dua buah titik data dengan garis lurus

4. Diketahui nilai suatu fungsi di titik x0 dan x1, yaitu f (x0) dan f (x1). Dengan metode interpolasi linier akan dicari nilai fungsi di titik x, yaitu f1(x). Indeks 1 pada f1(x) menunjukkan bahwa interpolasi dilakukan dengan interpolasi polinomial order satu.

5. Dari dua segitiga sebangun ABC dan ADE seperti tampak dalam Gambar, terdapat hubungan berikut:

6. Interpolasi LagrangeInterpolasi polinomial Lagrange hampir sama dengan polinomial Newton, tetapi tidak menggunakan bentuk pembagian beda hingga. Interpolasi polinomial Lagrange dapat diturunkan dari persamaan Newton.f1(x) = f (x0) + (x – x0) f [x1, x0]

7. Pembagian beda hingga yang ada dalam persamaan diatas mempunyai bentuk:

8. Substitusi persamaan interpolasi polinomial Lagrange order satu

9. interpolasi order dua Bentuk umum interpolasi polinomial Lagrange order n adalah

11. >>> [evaluate untitled-2.py]x Rational Neville0.10 -1.53420 -1.534200.15 -1.27164 -1.278710.20 -1.08110 -1.081100.25 -0.93119 -0.925350.30 -0.80687 -0.799200.35 -0.70003 -0.693560.40 -0.60587 -0.601910.45 -0.52136 -0.519830.50 -0.44450 -0.444500.55 -0.37388 -0.37432

12. TERIMA KASIH20/01/2011© 2010 Universitas Negeri Jakarta | www.unj.ac.id |12