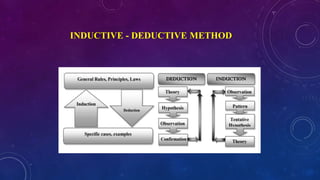
The document discusses inductive, deductive, analytic, and synthetic methods of reasoning. The inductive method involves presenting examples, making observations, and generalizing conclusions. The deductive method starts with general principles and applies them to specific cases. The analytic method breaks down problems into simpler parts, moving from unknown to known. The synthetic method combines known facts to derive new conclusions, moving from known to unknown. Examples are provided to illustrate the differences between the four methods.

1. INDUCTIVE
AND
DEDUCTIVE METHOD
By-
Monali Madhuchhanda Pradhan

2. INDUCTIVE METHOD
• Joseph Landon has said, “We make use of the inductive method whenever
we place before children a number of facts, examples or objects and then
endeavor to lead them to draw their own conclusions.”

3. INDUCTIVE METHOD
1. CONCRETE ABSTRACT
2. PARTICULAR GENERAL
3. EXAMPLE FORMULA
4. KNOWN UNKNOWN
5. SIMPLE COMPLEX
PRINCIPLE:

4. STEPS INVOLVED:
1. PRESENTATION OF EXAMPLES
2. OBSERVATIONS
3. GENERALIZATION
4. TESTING AND VERIFICATION

5. • EXAMPLE 1
1(a) 1(b)
Particular: Particular:
• Case 1: 12 = 1 Case 4: 22 = 4
• Case 2: 32 = 9 Case 5: 42 = 16
• Case 3: 52 = 25 Case 6: 62 = 36
General : General:
Square of an ODD number is ODD. Square of an EVEN number is EVEN.

6. EXAMPLE 2
Particular Cases:
• Case 1: 1 + 1 = 2(odd + odd = even)
• Case 2: 1 + 3 = 4(odd + odd = even)
• Case 3: 1 + 5 = 6(odd + odd = even)
• Case 4: 2 + 2 = 4(Even + even = even)
• Case 5: 4 + 4 = 8(Even + even = even)
• Case 6: 6 + 6 =12(Even + even = even)
Observe all the above cases,
General concept:
 From cases 1 to 3, we make a generalization
SUM OF TWO ODD NUMBER IS ALWAYS EVEN.
 From cases 4 to 6, we make a generalization
SUM OF TWO EVEN NUMBER IS ALWAYS EVEN.

7. DEDUCTIVE METHOD
PRINCIPLE:
1. ABSTRACT CONCRETE
2. GENERAL PARTICULAR
3. FORMULA EXAMPLE
4. UNKNOWN KNOWN
5. COMPLEX SIMPLE

8. STEPS INVOLVED:
1. Clear recognition of the problem
2. Search for a tentative hypothesis
3. Formulating of a tentative hypothesis
4. Verification

9. EXAMPLE 1:
Q. Find a2 × a3 = ?
Sol.
General:
From the law of indices, it is known that
am × an = a m+n
Particular:
Hence a2 × a3 = a2+3 = a5
(here m = 2 and n = 3)

10. • EXAMPLE 2:
Q. Find (102)2 = ?
Sol.
General :
We know that (a + b)2 = a2 + b2 + 2ab
Particular:
(100 + 2)2 = 1002 + 22 + (2 × 100 × 2)
(in this case a = 100 and b = 2)
= 10000 + 4 + 400 = 10404
We can also multiply 102 with itself to get the same result (for verification of the correctness of the earlier
result)

11. INDUCTIVE METHOD
Merits:
 Scientific method.
 Based on actual observation.
 Discourages habit of memorizing.
 Enhances self- confidence.
 Suitable in the beginning stage.
 Based on the principle of learning by doing.
Demerits:
 Application is limited to very few topics.
 Time consuming and laborious
 Less subject matter is covered.
 Not absolutely conclusive.

12. DEDUCTIVE METHOD
Merits:
 Short and time saving method
 Suitable for all the mathematical topics and
concepts.
 Useful for revision and drill work
 Enhance the power of learner’s memory
 Increases learner’s speed of work and efficiency
Demerits:
 Not a scientific method
 Encourages rote memory
 Not suitable for beginners.
 Students are only passive listeners.
 Lesson looks irrelevant and uninteresting
 Fails to develop self confidence.

13. DIFFERENCE BETWEEN INDUCTIVE AND DEDUCTIVE METHOD

14. INDUCTIVE - DEDUCTIVE METHOD

15. ANALYTIC
AND
SYNTHETIC METHOD
By-
Monali Madhuchhanda Pradhan

16. ANALYTIC METHOD
• “Analytic” ‘analysis’ to break or resolve a thing into its constituent elements.
• breaking up the unknown problem into simpler parts.
• From unknown to known

17. SYNTHETIC METHOD
• Opposite of analytic.
• “synthetic” ‘synthesis’ combine together.
• Combination of known facts to find new facts
• From known to unknown

18. EXAMPLE 1:

20. Example 2:
if a2+b2=7ab prove that 2log (a+b) = 2log3+loga+logb
Proof:
To prove this using analytic method, begin from the unknown.
The unknown is 2log (a+b) = 2log3+loga+logb
Now, 2log (a+b) = 2log 3+ log a+ log b is true
If log (a+b)2 = log 32 + log a + log b is true
If log (a+b)2 = log 9 + log ab is true
If log (a+b)2 = log 9ab is true
If (a+b)2 = 9ab is true
if a2+b2=7ab which is known and true
Thus if a2+b2= 7ab ,it is proved that 2log (a+b) = 2log3+loga+logb

21. if a2+b2=7ab prove that 2log (a + b) = 2log3+loga+logb
Proof:
To prove this using synthetic method, begin from the known.
The known is a2+b2= 7ab
Adding 2ab on both sides
a2+b2+2ab=7ab + 2ab
(a+b)2 = 9ab
Taking log on both sides
log (a+b)2 = log 9ab
2log (a+b) = log 9 + log ab
2 log (a+b) = log 32 + log a + log b
2log (a+b) = 2log 3+ log a+ log b
Thus if a2+b2=7ab , it is proved that 2log (a+b) = 2log3+loga+logb

22. ANALYTIC METHOD
Merits:
 Logical method.
 Thinking and reasoning power enhances.
 Scientific originality and creativity.
 Develops self- confidence.
 Logical approach to prove proposition and
statements
 Active participation
 Learners get clear understanding
Demerits:
 lengthy method
 Application is limited to very few topics
 Not suitable to all age groups
 Not suitable at lower stage
 Time consuming
 This method has slow speed.

23. SYNTHETIC METHOD
Merits:
 Product of thoughts
 Parts to whole
 Systematic presentation of facts
 Saves time
 Accuracy
 Provides necessary skill speed and
efficiency
 Learners benefitted
Demerits:
 Possibility of forgetting
 No active participation of student
 Least confidence
 Increases the elements of doubt
 Discovery is not possible

24. Difference Between Analytic And Synthetic Method