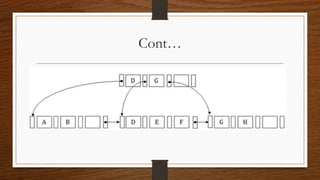
The document discusses different file structures and indexing techniques used in databases. It describes secondary keys as keys that are not selected as the primary key but are candidate keys. It then explains inverted and multi-user files, and different file organization methods like sequential, heap, hash, and B-tree organizations. It provides details on B-trees and B+trees, including their properties, time complexities for operations, and structure for internal and leaf nodes in B+trees.

1. File Structures(Part 2)
BY:SURBHI SAROHA

2. Syllabus
• Secondary key Retrieval:
• Inverted and multiuser files
• Indexing Using Tree Structures:
• B-trees
• B+trees

3. Secondary key Retrieval
• Secondary Key is the key that has not been selected to be the primary key.
However, it is considered a candidate key for the primary key.
• Therefore, a candidate key not selected as a primary key is called secondary
key.
• Candidate key is an attribute or set of attributes that you can consider as a
Primary key.
• Note: Secondary Key is not a Foreign Key.

4. Example
Student_ID Student_Enr
oll
Student_Na
me
Student_Age Student_
Email
096 9122717 Manish 25 aaa@gmai
l.com
055 9122655 Manan 23 abc@gmai
l.com
067 9122699 Shreyas 28 pqr@gmai
l.com
Example
Let us see an example −

5. Cont….
• Above, Student_ID, Student_Enroll and Student_Email are the candidate keys.
• They are considered candidate keys since they can uniquely identify the student
record.
• Select any one of the candidate key as the primary key. Rest of the two keys would
be Secondary Key.
• Let’s say you selected Student_ID as primary key,
therefore Student_Enroll and Student_Email will be Secondary Key (candidates
of primary key).

6. Inverted and multiuser files
• A database consist of a huge amount of data. The data is grouped within a table in RDBMS,
and each table have related records. A user can see that the data is stored in form of tables,
but in acutal this huge amount of data is stored in physical memory in form of files.
• File – A file is named collection of related information that is recorded on secondary
storage such as magnetic disks, magnetic tables and optical disks.
• What is File Organization?
File Organization refers to the logical relationships among various records that constitute
the file, particularly with respect to the means of identification and access to any specific
record. In simple terms, Storing the files in certain order is called file Organization. File
Structure refers to the format of the label and data blocks and of any logical control
record.

7. Cont….
• Types of File Organizations –
• Various methods have been introduced to Organize files. These particular methods have
advantages and disadvantages on the basis of access or selection . Thus it is all upon the
programmer to decide the best suited file Organization method according to his requirements.
Some types of File Organizations are :
• Sequential File Organization
• Heap File Organization
• Hash File Organization
• B+ Tree File Organization
• Clustered File Organization

8. Indexing Using Tree Structures:
• B-trees
• B-Tree is a self-balancing search tree. In most of the other self-balancing search trees
(like AVL and Red-Black Trees), it is assumed that everything is in main memory. To understand
the use of B-Trees, we must think of the huge amount of data that cannot fit in main memory.
When the number of keys is high, the data is read from disk in the form of blocks. Disk access
time is very high compared to the main memory access time. The main idea of using B-Trees is
to reduce the number of disk accesses. Most of the tree operations (search, insert, delete, max,
min, ..etc ) require O(h) disk accesses where h is the height of the tree. B-tree is a fat tree. The
height of B-Trees is kept low by putting maximum possible keys in a B-Tree node. Generally, the
B-Tree node size is kept equal to the disk block size. Since the height of the B-tree is low so total
disk accesses for most of the operations are reduced significantly compared to balanced Binary
Search Trees like AVL Tree, Red-Black Tree, ..etc.

9. Time Complexity of B-Tree:
• Sr. No. Algorithm Time Complexity
• 1. Search O(log n)
• 2. Insert O(log n)
• 3. Delete O(log n)

10. Properties of B-Tree:
• All leaves are at the same level.
• A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
• Every node except root must contain at least (ceiling)([t-1]/2) keys. The root may contain minimum 1 key.
• All nodes (including root) may contain at most t – 1 keys.
• Number of children of a node is equal to the number of keys in it plus 1.
• All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in
the range from k1 and k2.
• B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow
downward and also shrink from downward.
• Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(log n).

11. B+trees
• The B+ tree is a balanced binary search tree. It follows a multi-level index
format.
• In the B+ tree, leaf nodes denote actual data pointers. B+ tree ensures that
all leaf nodes remain at the same height.
• In the B+ tree, the leaf nodes are linked using a link list. Therefore, a B+
tree can support random access as well as sequential access.

12. Structure of B+ Tree
• In the B+ tree, every leaf node is at equal distance from the root node. The
B+ tree is of the order n where n is fixed for every B+ tree.
• It contains an internal node and leaf node.

13. Cont…

14. Internal node
• An internal node of the B+ tree can contain at least n/2 record pointers except the root
node.
• At most, an internal node of the tree contains n pointers.
• Leaf node
• The leaf node of the B+ tree can contain at least n/2 record pointers and n/2 key values.
• At most, a leaf node contains n record pointer and n key values.
• Every leaf node of the B+ tree contains one block pointer P to point to next leaf node.
•

15. Thank you