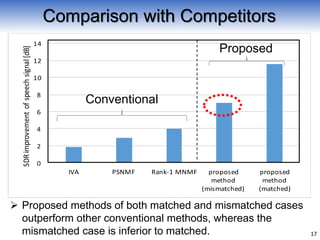
This document proposes a flexible microphone array system using informed source separation methods for a rescue robot. It aims to detect victim speech in disaster areas using multiple microphones on the robot's flexible body. The proposed method uses supervised rank-1 nonnegative matrix factorization (NMF) and statistical signal estimation to address two key problems: ego-noise basis mismatch due to the robot's self-vibrations, and speech model ambiguity. Experiments show the proposed approach outperforms conventional independent vector analysis and single-channel NMF, improving speech detection even with mismatched ego-noise recordings.

1. Flexible Microphone Array Based on
Multichannel Nonnegative Matrix Factorization
and Statistical Signal Estimation
Hiroshi Saruwatari, Kazuma Takata
(The Unoversity of Tokyo, JAPAN)
Nobutaka Ono (NII, JAPAN),
Shoji Makino (University of Tsukuba, JAPAN)
Acoustic Array Systems: Paper ICA2016-312

2. Outline
 Introduction of rescue robot audition
 Conventional approaches (ICA, IVA, Rank-1
MNMF)
 Informed source separation and its problem
 Ego-noise basis mismatch problem solution
 Speech ambiguity problem solution
 Experimental evaluation
 Conclusion
2

3. Introduction: Rescue Robot Audition
 Aimed to detect victims’ speech in a disaster area.
 Flexible body twists and moves driven by vibration motors.
 It wears multiple microphones around the body.
• Thus, microphones’ position is always unknown.
• Self-Vibration generates harmful noise.
(so-called Ego-Noise)
One of the Distributed Microphone Array Problem
3
MicrophoneVibrator
What is hose-shaped rescue robot?

4. 4
Source Observation Separated
Mixing Separation
Conventional: ICA or Independent vector analysis (IVA), which
separates the sources based on their independence nature.
We assume
linear time-
invariance in A.
This is a simultaneous
estimation problem for
W and source
statistical models.
x=As y=Wx
Unknown Known
W
Demixing
matrix
How to solve? Use Blind Source Separation
Source model (p.d.f.s)
S1
S2
Speech
Ego-noise
Speech
Ego-
noise
+

5. Low-rank source spectrogram
5
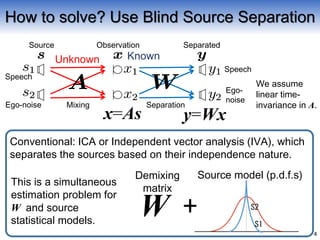
Rank-1 MNMF (Independent Low-Rank Matrix Analysis)
that separates the sources by estimating demixing matrix W
and low-rank source spectrogram model via Nonnegative
Matrix Factorization (NMF) [Lee, 2001].
Rank-1 MNMF [Kitamura, Saruwatari et al., IEEE Trans. ASLP 2016]
W
Demixing
matrix
Simultaneous
estimation for W
and TV
+
In this study, we focus our attention to…

6. 6
Rank-1 MNMF (Independent Low-Rank Matrix Analysis)
Pros & Cons:
• All parameters can be updated via Auxiliary-Function method
(EM-like algorithm), keeping nonnegative feature of T & V.
• The cost function always decreases in each iteration. Thus,
this is convergence-guaranteed algorithm unlike ICA!
• Still affected by initial state of parameters. go to “Informed”
Rank-1 MNMF’s cost function to be minimized
: Independence measure between sources (for W)
: Low-rank approximation of sources (for T and V)
(Note: both are based on Itakura-Saito (IS) divergence.)

7. Typical ego-noise
basis trained by
NMF in advance
Activation
Source model in Rank-1 MNMF
7
Basis
Toward Informed Source Separation

8. Typical ego-noise
basis trained by
NMF in advance
Activation
Source model in Rank-1 MNMF
Fixing a part of bases, estimate
remaining parameters and W.
8
Basis
Speech
basis
Ego-
noise
basis
Toward Informed Source Separation
(unknown)
(unknown)

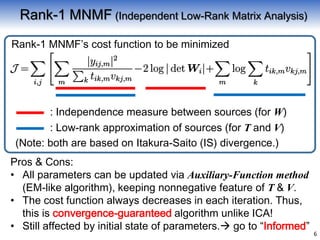
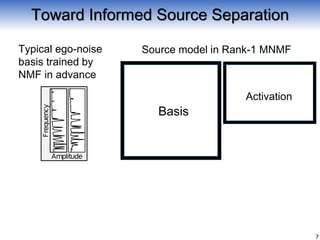
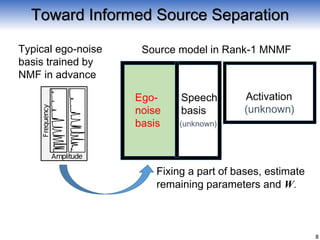
9. Typical ego-noise
basis trained by
NMF in advance
Activation
Source model in Rank-1 MNMF
Fixing a part of bases, estimate
remaining parameters and W.
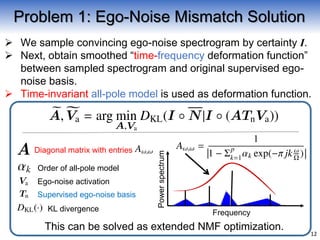
[Problem 1] Ego-noise time-variance (ego-noise mismatch problem)
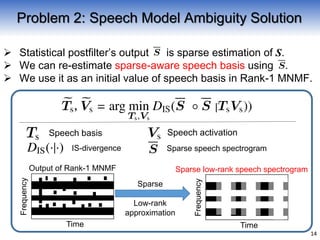
[Problem 2] Unknown speech (speech model ambiguity problem)
9
Basis
Speech
basis
Ego-
noise
basis
Toward Informed Source Separation
(unknown)
(unknown)

10. Supervised Rank-1 MNMF
Rough separation
Statistical Postfilter [Breithaupt, 2010]
 Chi distribution (sparse p.d.f.)
is used as target signal prior.
 Its sparseness can be estimted
from data empirically via
higher-order statistics
[Murota, Saruwatari, ICASSP2014].
Observed
signal
Thanks to sparse prior, we can
obtain more accurate separation
and its Certainty.
Statistical Signal Estimation
Certainty
Estimated ego-noise
Sparse p.d.f.
6
Estimated target signal

11. Statistical Signal Estimation
6
Certainty I ={1; if G(f,t)>0.8, otherwise 0}: binary mask that
extracts seldom overlapping components with the target signal
from the estimated interference signal.

12. 12
Problem 1: Ego-Noise Mismatch Solution
 We sample convincing ego-noise spectrogram by certainty I.
 Next, obtain smoothed “time-frequency deformation function”
between sampled spectrogram and original supervised ego-
noise basis.
 Time-invariant all-pole model is used as deformation function.
Diagonal matrix with entries
Supervised ego-noise basis
Ego-noise activation
KL divergence
Order of all-pole model
This can be solved as extended NMF optimization.
Frequency
Powerspectrum

13. 13
Problem 1: Ego-Noise Mismatch Solution
: each element of
Update of activation
Update of all-pole-model weight
By noting the KL-cost function as J, its auxiliary function is given by

14.  Statistical postfilter’s output is sparse estimation of S.
 We can re-estimate sparse-aware speech basis using .
 We use it as an initial value of speech basis in Rank-1 MNMF.
14
Problem 2: Speech Model Ambiguity Solution
Speech basis Speech activation
IS-divergence
Time
Frequency
Time
Frequency
Sparse low-rank speech spectrogramOutput of Rank-1 MNMF
Sparse
Low-rank
approximation
Sparse speech spectrogram

15. 実験条件
 # of mic. : 8 channel microphones on 3-m-long hose-shape robot
 Speech : male & female speech with real-recorded impulse responses
 Ego-noise: real-recorded in moving hose-shaped robot (2 patterns)
 Training : matched with mixed ego-noise (2 patterns) &
mismatched (3 patterns)
 Evaluation: SDR improvement (both SNR and distortion are considered)
 Input SDR: 0 dB, -5 dB, -10 dB
 Comparison: IVA, PSNMF (single-channel supervised NMF),
Rank-1 MNMF (no supervision)
15
Simulation Experiment
True target Interference Artificial distortionEstimated
Higher SDR
indicates better
separation

16. 16
Example of Typical SDR Improvement
Supervised
Rank-1
MNMF
Statistical
postfilter
(1)
(2)
(3)
(4)
Combination of each processing is effective.
SDRImprovement[dB]
Step(1) Step(2) Step(3) Step(4)
SDR increases through
each processing step
Before basis defom.
and initialization
Basis
deform.
and
Initialization
After basis defom.
and initialization

17. 17
Comparison with Competitors
 Proposed methods of both matched and mismatched cases
outperform other conventional methods, whereas the
mismatched case is inferior to matched.
Conventional
Proposed

18.  We proposed a new informed source separation
method for the flexible microphone array system based
on supervised Rank-1 MNMF and statistical speech
enhancement.
 To reduce the mismatch problem, we proposed the
algorithm that an all-pole model is estimated to deform
the bases using the reliable spectral components
sampled by the statistical signal enhancement method.
 We revealed that the proposed method outperforms the
conventional methods via experiments with actual
sounds in the rescue robot.
18
Conclusion
Thank you for your attention!