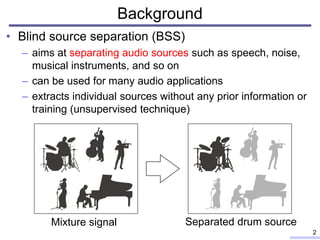
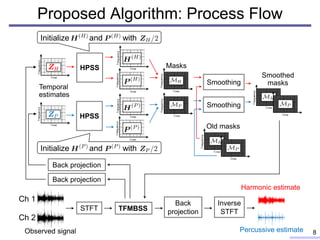
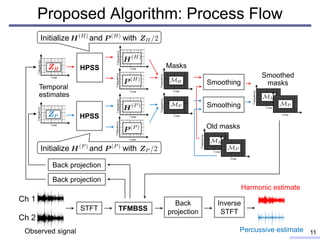
This document proposes a new method for linear multichannel blind source separation (BSS) based on time-frequency masks obtained from harmonic/percussive sound separation (HPSS). The proposed method applies HPSS independently to temporarily estimated sources to generate harmonic and percussive masks, then smooths the masks and uses them in time-frequency masking-based BSS. Experiments show the proposed method achieves higher source separation quality than single-channel HPSS and outperforms other multichannel BSS methods, demonstrating the effectiveness of integrating HPSS with multichannel BSS.

1. Linear multichannel blind source separation
based on time-frequency mask obtained by
harmonic/percussive sound separation
Oyabu Soichiro1, Daichi Kitamura1, and Kohei Yatabe2
1National Institute of Technology, Kagawa College, Japan
2The University of Waseda, Japan
2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)

2. Background
• Blind source separation (BSS)
– aims at separating audio sources such as speech, noise,
musical instruments, and so on
– can be used for many audio applications
– extracts individual sources without any prior information or
training (unsupervised technique)
2
Mixture signal Separated drum source

3. • Multichannel BSS
– estimates demixing system (inverse system of )
– High separation quality because of spatial information
• Independent vector analysis (IVA) [Kim+, 2007]
• Independent low-rank matrix (ILRMA) [Kitamura+, 2016]
• Time-frequency-masking-based BSS (TFMBSS) [Yatabe+, 2019]
• Single-channel BSS
– Monaural audio source separation problem
– More difficult than multichannel BSS
• Harmonic/percussive sound separation (HPSS) [Ono+, 2008]
Background
3
Mixing system Demixing system

4. Background
• HPSS [Ono+, 2008], [FitzGerald, 2010], [Duong+, 2011], [Tachibana+, 2012], etc.
– separates harmonic and percussive sound sources in a
fully blind manner
– can be used for music analysis and remixing
• Ex. estimation of chords, tempo, rhythm, notes, and genre
4
Mixture signal
Harmonic estimate
Percussive estimate
Aim: high-quality multichannel blind HPSS

5. Source Models in BSS
• In BSS, assumption of time-frequency structure in
each source (source model) is required
– IVA [Kim+, 2007]
• All the frequencies of each source
simultaneously have large power
• Linear spatial demixing
– ILRMA [Kitamura+, 2016]
• Power spectrogram of each source
have a low-rank time-frequency
structure
• Linear spatial demixing
– HPSS [Ono+, 2008], [Tachibana+, 2012]
• Harmonic: time-continuous structure
• Percussive: freq.-continuous structure
• Non-linear separation
5
Freq.
Freq.
Freq.
Time
Time
Time
Percussive src.
Harmonic src.
Source2
Source１
Source2
Source１

6. Conventional Method: TFMBSS [Yatabe+, 2019]
• Time-frequency-masking-based BSS (TFMBSS)
– Linear multichannel BSS with plug-and-play source models
– Source model is input as a time-frequency mask
6
Generate time-frequency
mask based on temporal
estimated sources
Masking process
: entrywise product

7. • Harmonic/percussive sound separation (HPSS)
– Separate sources by focusing on “smoothness” along with
time or frequency directions in spectrogram
– Estimate and by iteratively minimizing the cost function
Conventional Method: HPSS [Ono+, 2008]
7
Harmonic estimate
Mixture signal
Harmonic
components
Percussive
components
Time
Frequency
Percussive estimate

8. Proposed Algorithm: Process Flow
8
Inverse
STFT
STFT
Back
projection
Smoothing
Smoothing
HPSS
HPSS
Old masks
Initialize and with
Initialize and with
Back projection
Back projection
Observed signal Percussive estimate
Harmonic estimate
Masks
TFMBSS
Smoothed
masks
Ch 1
Ch 2
Temporal
estimates

9. • Two HPSS are independently
applied to each of temporarily
estimated signals and
• Two Wiener-like masks and , are
constructed using the results of HPSS
– These masks enhance the harmonic or percussive
components by eliminating the other components
Proposed Algorithm: Mask Calculation
9
HPSS
HPSS

10. Proposed Algorithm: Mask Smoothing
10
• In TFMBSS, drastic change of masks in each
iteration will cause instability of parameter
optimization
• Introduce mask smoothing process based on
weighted geometric mean
– Intensity of smoothing can be controlled by and
Mask calculated in
the previous iteration
Mask calculated in
the current iteration
Entrywise
product

11. Proposed Algorithm: Process Flow
11
Inverse
STFT
STFT
Back
projection
Smoothing
Smoothing
HPSS
HPSS
Old masks
Initialize and with
Initialize and with
Back projection
Back projection
Observed signal Percussive estimate
Harmonic estimate
Masks
TFMBSS
Smoothed
masks
Ch 1
Ch 2
Temporal
estimates

12. • Mixing condition of dry sources
Experiments: Conditions
12
Music Dataset
(dry sources)
SiSEC2016 MUS [Liutkus+, 2016]
“Drums” and “Other” sources of 20 songs
Windowing in STFT 128-ms-long Hann window with half-overlap shifting
Number of iterations
in TFMBSS
500
Subjective evaluation
score
Improvement of source-to-distortion ratio
(SDR) [Vincent+, 2006]
2 m
5.66cm
50 50
Impulse response E2A in RWCP database [Nakamura+, 2000]
(reverberation time: 300 ms)
Other source
(harmonic)
Drum source
(Percussive)

13. Experiment 1: Conditions
• Investigate the optimal number of iterations in HPSS
blocks
• Compare average SDR imp. of the proposed method
13

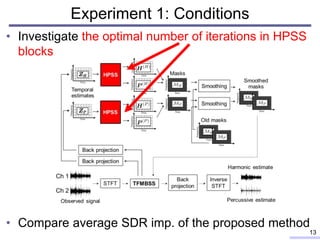
14. • Average SDR improvements of the proposed method
with various numbers of iterations in HPSS blocks
0
2
4
6
8
10
12
1 3 5 7 9 11 13 15 20
Average
SDR
improvements
[dB]
Number of iterations in HPSS blocks
Experiment 1: Results
14

15. Experiment 2: Conditions
• Investigate the optimal smoothing parameter
• Compare average SDR imp. of the proposed method
15

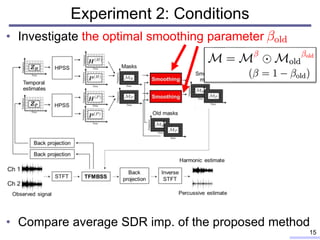
16. • Typical example of SDR behaviors in the proposed
method with various smoothing parameters
-2
0
2
4
6
8
10
12
14
16
0 100 200 300 400 500
SDR
improvements
[dB]
Numbers of iterations of proposed method
βold=0
βold=0.5
βold=0.75
βold=0.875
βold=0.9375
Experiment 2: Results
16

17. 0
2
4
6
8
10
12
0 0.5 0.75 0.875 0.9375
Average
SDR
improvements
[dB]
Smoothing parameter
Experiment 2: Results
17
• Average SDR improvements of the proposed method
with various smoothing parameters

18. Experiment 3: Conditions
• Compare proposed method with five BSS methods
– Single-channel HPSS [Ono+, 2008] , [Tachibana+, 2010], [Tachibana+, 2012]
– Multichannel HPSS [Duong+, 2011]
– AuxIVA [Ono+, 2011]
– ILRMA [Kitamura+, 2016]
– Proposed method
18

19. • Average SDR improvement for HPSS and BSS
algorithms
Experiment 3: Results
0
2
4
6
8
10
12
Single-channel
HPSS
Multichannel
HPSS
AuxIVA ILRMA Proposed
method
Average
SDR
improvements
[dB]
Linear multichannel BSS
Non-linear
single-channel
BSS
19

20. • Music sample: SiSEC2016 Forkupines - Semantics
Demonstration
20
Observed
mixture
Single-
channel
HPSS
AuxIVA ILRMA
Proposed
method
Estimated harmonic sources
Estimated percussive sources

21. Conclusion
• Novelty
– Integration of conventional HPSS with TFMBSS
– Wiener-filter-based iterative mask update
– Iterative mask smoothing for stabilizing optimization
• Results
– Mask smoothing process drastically stabilizes the TFMBSS
optimization and improves the separation performance
– Achieved high-quality linear multichannel HPSS
21
Thank you for your attention!