The document discusses blind source separation (BSS) techniques, focusing on independent low-rank matrix analysis (ILRMA) for separating audio signals without prior information on recording conditions. It outlines the evolution of BSS methods such as frequency-domain independent component analysis (FDICA) and independent vector analysis (IVA), and highlights the advantages of ILRMA in improving optimization and separation accuracy. Additionally, it details the relationship between ILRMA and multichannel nonnegative matrix factorization (NMF), including a comparative analysis of different source models.



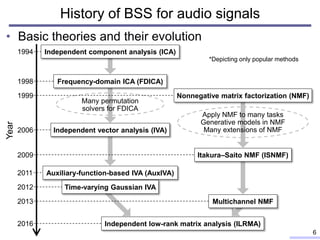
![Motivation of ILRMA
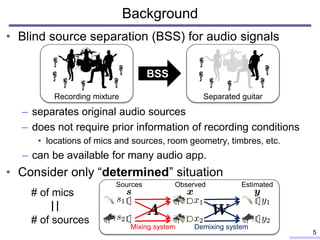
• Conventional BSS techniques based on ICA
– Minimum distortion (linear demixing)
– Relatively fast and stable optimization
• FastICA [A. Hyvarinen, 1999], natural gradient [S. Amari, 1996], and auxiliary
function technique [N. Ono+, 2010], [N. Ono, 2011]
– Could not use “specific” assumption of sources
• Only assumes non-Gaussian p.d.f. for sources
– Permutation problem is crucial and still difficult to solve
• IVA often fails causing a “block permutation problem” [Y. Liang+, 2012]
• Better to use a “specific source model” in TF domain
– Independent low-rank matrix analysis (ILRMA) employs
a low-rank property 7
: frequency bins
Observed
signal
Source signalsFrequency-wise mixing matrix
: time frames
Estimated
signal
Frequency-wise demixing matrix](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-7-320.jpg)

![• Independent component analysis (ICA)[P. Comon, 1994]
– estimates without knowing
– Source model (scalar)
• is non-Gaussian and mutually independent
– Spatial model
• Mixing system is a time-invariant matrix
• Mixing system in audio signals
– Convolutive mixture with room reverberation
Related methods: ICA
9
Mixing
matrix
Demixing
matrix
Source model
Sources Observed Estimated
Spatial model](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-9-320.jpg)
![• Frequency-domain ICA (FDICA) [P. Smaragdis, 1998]
– estimates frequency-wise demixing matrix
– Source model (scalar)
• is complex-valued,
non-Gaussian, and
mutually independent
– Spatial model
• Frequency-wise mixing
matrix is time-invariant
– Instantaneous mixture in each frequency band
– A.k.a. rank-1 spatial model [N.Q.K. Duong, 2010]
• Permutation problem?
– Order of estimated signals cannot be determined by ICA
– Alignment of frequency-wise estimated signals is required
• Many permutation solvers were proposed
Related methods: FDICA
10
Spectrograms
ICA1
…
Frequencybin
Time frame
…
ICA2
ICA I](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-10-320.jpg)
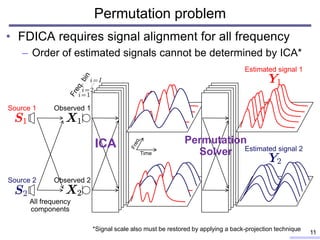
![Related methods: IVA
• Independent vector analysis (IVA)[A. Hiroe, 2006], [T. Kim, 2006]
– extends ICA to multivariate probabilistic model to consider
sourcewise frequency vector as a vector variable
– Source model (vector)
• is multivariate, spherical, complex-valued, non-Gaussian, and
mutually independent
– Spatial model
• Mixing system is a time-invariant matrix (rank-1 spatial model) 12
…
…
Mixing matrix
…
…
…
Observed vector
Demixing matrix
Estimated vector
Multivariate non-
Gaussian dist.
Have higher-order
correlations
Permutation-free estimation of is achieved!
Source vector](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-12-320.jpg)
![• Spherical multivariate distribution[T. Kim+, 2007]
• Why spherical distribution?
– Frequency bands that have similar activations will be merged
together as one source avoid permutation problem
Higher-order correlation assumed in IVA
13
x1 and x2 are mutually independent
Spherical
Laplace dist.
Mutually
independent two
Laplace dist.s
x1 and x2 have higher-order correlation
Probability depends on
only the norm](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-13-320.jpg)
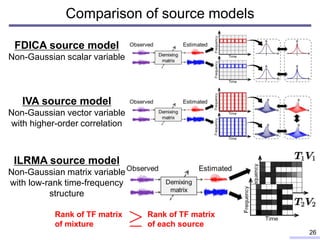
![• Frequency-domain ICA (FDICA) [P. Smaragdis, 1998]
• Independent vector analysis (IVA)[A. Hiroe, 2006], [T. Kim, 2006]
Comparison of source models
14
Observed
Update separation filter so that the estimated
signals obey non-Gaussian distribution we assumed
Estimated
Demixing
matrix
Current
empirical dist.
Non-Gaussian
source dist.
STFT
Frequency
Time
Frequency
Time
Observed Estimated
Current
empirical dist.
STFT
Frequency
Time
Frequency
Time
Non-Gaussian
spherical
source dist.
Scalar r.v.s
Vector
(multivariate) r.v.s
Update separation filter so that the estimated
signals obey non-Gaussian distribution we assumed
Mixture is close to Gaussian
signal because of CLT
Source obeys non-
Gaussian dist.
Mutually
independent
Demixing
matrix Mutually
independent](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-14-320.jpg)
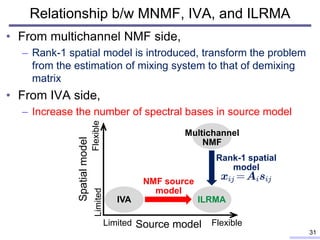
![Related method: NMF
• Nonnegative matrix factorization (NMF) [D. D. Lee, 1999]
– Low-rank decomposition with nonnegative constraint
• Limited number of nonnegative bases and their coefficients
– Spectrogram is decomposed in acoustic signal processing
• Frequently appearing spectral patterns and their activations
15
Amplitude Amplitude
Nonnegative matrix
(power spectrogram)
Basis matrix
(spectral patterns)
Activation matrix
(time-varying gains)
Time
: # of freq. bins
: # of time frames
: # of bases
Time
Frequency
Frequency](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-15-320.jpg)
![• ISNMF[C. Févotte, 2009]
– can be decomposed using “stable property” of
• If we define ,
Related method: ISNMF
16
Equivalent Circularly symmetric complex Gaussian dist.
Complex-valued observed signal
Nonnegative variance
Variance is also decomposed!](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-16-320.jpg)
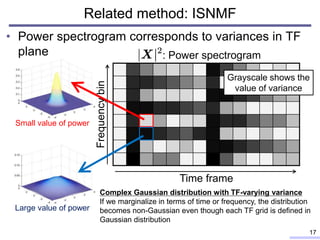
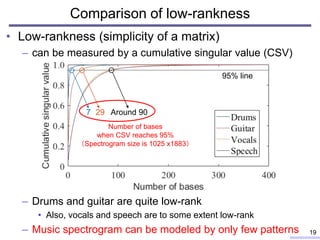

![Extension of source model in IVA
• Source model in IVA
– has a frequency-uniform scale
• Spherical multivariate Laplace
• Higher-order correlation among frequency
– Equivalent to NMF with one flat basis
• Source model in ISNMF[C. Févotte+, 2009]
– NMF with arbitrary number of bases
• can represent complicated TF structures
– can learn “co-occurrence” structure
in TF domain for each source
• Low-rank co-occurrence is captured as the variance
– The source-wise structure can be
estimated by ISNMF 21
Frequency
Time
Frequency
Time
Replace the source model
assumed in ICA or IVA](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-21-320.jpg)
![• Source model in IVA
• Source model in ISNMF[C. Févotte+, 2009]
22
Frequency-uniform scale
Extension of source model in IVA
Zero-mean complex
Gaussian in each TF bin
Low-rank decomposition
with NMF
Spherical Laplace dist.
(bivariate case)
Frequency vector
(I-dimension)
Time-frequency-varying variance
Time-frequency matrix
(IJ-dimensional)
Replace the source model
assumed in ICA or IVA](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-22-320.jpg)
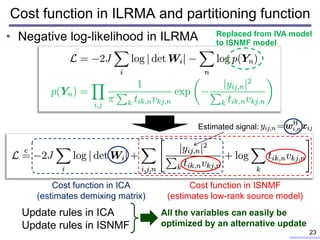
![Update rules of ILRMA
• ML-based iterative update rules
– Update rule for is based on iterative projection [N. Ono, 2011]
– Update rules for NMF variables is based on MM algorithm
– Pseudo code is available at
• http://d-kitamura.net/pdf/misc/AlgorithmsForIndependentLowRankMatrixAnalysis.pdf 24
Spatial model
(demixing matrix)
Source model
(NMF source model)
where
and is a one-hot vector
that has 1 at th element](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-24-320.jpg)
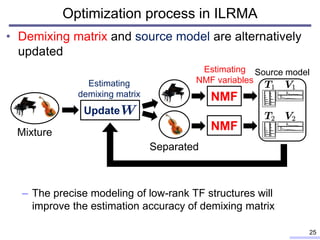
![• Multichannel NMF[A. Ozerov+, 2010], [H. Sawada+, 2013]
Multichannel extension of NMF
27
Spatial covariances in
each time-frequency slot
Observed
multichannel signal
Spatial covariances
of each source Basis matrix Activation matrix
Spatial model Source model
Partitioning function
Spectral patterns
Gains
Spatial property of each source Timber patterns of all sources
Multichannel
vector
Instantaneous spatial covariance](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-27-320.jpg)



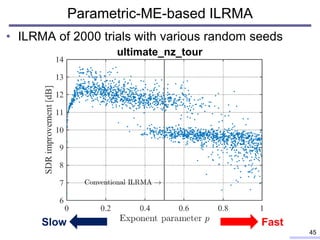
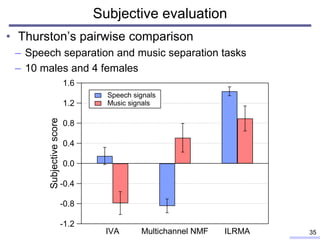
![• Ultimate NZ tour (Guitar and Synthesizer, 14s)
Result example
33
Poor
Good 20
15
10
5
0
SDRimprovement[dB] Guitar
Synth.
IVA Multichannel
NMF
ILRMA](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-32-320.jpg)
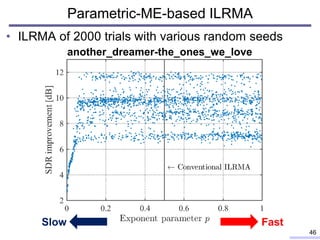
![• Ultimate NZ tour (Guitar and Synthesizer, 14s)
12
10
8
6
4
2
0
-2
SDRimprovement[dB]
4003002001000
Iteration steps
IVA
MNMF
ILRMA
ILRMA
Results: bearlin-roads
34
without Z
with Z
11.5 s
15.1 s 60.7 s
7647.3 s
Poor
Good](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-33-320.jpg)
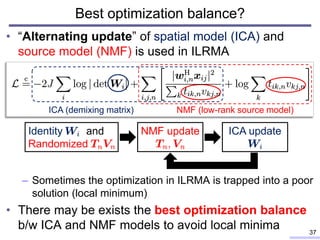
![Majorization-based optimization algorithm
• NMF optimization is based on a majorizer-based
algorithm (a.k.a. auxiliary function technique)
– Majorization-minimization (MM) algorithm [D. R. Hunter+, 2000]
39](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-38-320.jpg)
![Majorization-based optimization algorithm
• NMF optimization is based on a majorizer-based
algorithm (a.k.a. auxiliary function technique)
– Majorization-minimization (MM) algorithm [D. R. Hunter+, 2000]
40](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-39-320.jpg)
![Majorization-based optimization algorithm
• NMF optimization is based on a majorizer-based
algorithm (a.k.a. auxiliary function technique)
– Majorization-equalization (ME) algorithm [C. Févotte+, 2011]
41](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-40-320.jpg)
![Majorization-based optimization algorithm
• NMF optimization is based on a majorizer-based
algorithm (a.k.a. auxiliary function technique)
– Majorization-equalization (ME) algorithm [C. Févotte+, 2011]
42
Fast Slow](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-41-320.jpg)
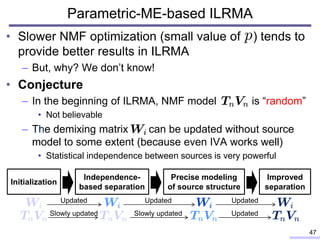
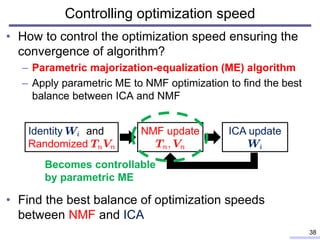
![Majorization-based optimization algorithm
• NMF optimization is based on a majorizer-based
algorithm (a.k.a. auxiliary function technique)
– Parametric ME algorithm [Y. Mitsui+, 2017]
43](https://image.slidesharecdn.com/kitamura2017ohiostateunivtalkver1slideshare-180209100603/85/Blind-source-separation-based-on-independent-low-rank-matrix-analysis-and-its-extensions-42-320.jpg)