The document discusses a method for sound field recording and reproduction that improves accuracy by using prior knowledge of primary source locations. It outlines the requirements and techniques necessary for signal conversion in various array geometries, showcasing simulation results that demonstrate the method's effectiveness compared to existing techniques. The proposed method shows a larger region of high reproduction accuracy when using cylindrical arrays of microphones and loudspeakers.

1. Source-Location-Informed Sound Field
Recording and Reproduction:
A Generalization to Arrays of Arbitrary
Geometry
Shoichi Koyama
The University of Tokyo / Université Paris Diderot (Institut Langevin)

2. July 19, 2016
Super-resolution in Recording and Reproduction
Improve reproduction accuracy when
less microphones than loudspeakers
 # of microphones > # of loudspeakers
– Higher reproduction accuracy within local region of target area
 # of microphones < # of loudspeakers
– Higher reproduction accuracy of sources in local region of recording area
[Koyama+ ICASSP 2014], [Koyama+ IEEE JSTSP 2015]
[Ahrens+ AES Conv. 2010]
Microphone array Loudspeaker array

3. Sound Field Recording and Reproduction
July 19, 2016
Recording area Target area
Obtain driving signals of secondary sources (= loudspeakers)
arranged on to reconstruct desired sound field inside
 Inherently, sound pressure and its gradient on is required to obtain
, but sound pressure is usually only known
 Fast and stable signal conversion for sound field recording and reproduction
with ordinary acoustic sensors and transducers is required
Primary
sources

4. July 19, 2016
Wave field reconstruction (WFR) filtering method
Target area
Received
signals
Driving signals
Plane wave Plane wave
Each plane wave determines entire sound field
Spatial aliasing artifacts due to plane wave decomposition
Significant error at high freq. even when microphone < loudspeaker
Recording area
[Koyama+ IEEE TASLP 2013]
Signal
conversion
Secondary source planeReceiving plane
Primary
sources

5. Source-Location-Informed Recording and Reproduction
 Signal conversion method that takes into account a priori knowledge of primary
source locations
 This prior information can be obtained by using various types of sensors or by
manual input
 By exploiting this prior information, reproduction accuracy above the spatial
Nyquist freq can be improved
 Apply the method proposed in [Koyama+ IEEE JSTSP 2015] to several array
geometries
July 19, 2016
Target areaRecording area
Signal
conversion
Secondary source planeReceiving plane
Primary
sources
Approximate location is
obtained by sensors

6. Statement of Problem
July 19, 2016
Target areaRecording area
Primary
sources
Secondary source distribution:
Microphone array on baffle
Control points
Constraint on driving signals
Linear combination of spatial basis functions
Transfer functionDesired
pressures
Optimize and by
using prior information on
source locations

7. Statement of Problem
July 19, 2016
Target areaRecording area
Primary
sources
Secondary source distribution:
Control points
 Two requirement must be satisfied to apply the method proposed in
[Koyama+ IEEE JSTSP 2015]
1. The relationship between and can be obtained
2. The amplitude distribution of the driving signals of the secondary
sources can be predicted from prior information on the source location
Microphone array on baffle

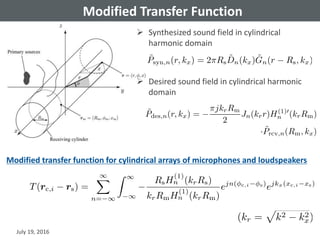
8. Modified Transfer Function
 For the first requirement, we consider modified transfer function
that relates with
 For planar / linear array case, because can
be equivalent to
 When microphones are mounted on baffle,
 We here show an example of a cylindrical array
– Spherical array case is presented in [Koyama+ WASPAA 2015]
July 19, 2016

9. Modified Transfer Function
 Synthesized sound field in cylindrical
harmonic domain
 Desired sound field in cylindrical harmonic
domain
July 19, 2016
Modified transfer function for cylindrical arrays of microphones and loudspeakers

10. MAP Estimation of Driving Signals
 Likelihood function: complex Gaussian distribution
 Prior distribution: Amplitude distribution of ( ) predicted from
approximate primary source location is incorporated
July 19, 2016
Maximum a posteriori (MAP) estimation
Bayes’ rule
Likelihood function Prior distribution

11. MAP Estimation of Driving Signals
 Objective function:
 Assume that spatial basis functions are M orthogonal functions, which
satisfies the following relation of singular value decomposition
 Optimal spatial basis functions and their coefficients
 Driving signals obtained by MAP estimation
July 19, 2016
( : regularization parameter)

12. Prior Based on Primary Source Locations
 Amplitude distribution can be obtained by assuming point
source at prior source location with sound field synthesis
techniques
 When array geometry is cylinder and estimated primary source
location is , predicted driving signal is
obtained as
July 19, 2016
Normalization

13. Algorithm
July 19, 2016
Discretize secondary source distribution
Amplitude distribution for prior

14. Algorithm
1. Detect source location ( )
2. Calculate amplitude distribution
3. Calculate as
4. Eigenvalue decomposition of
5. Obtain transform filter as
July 19, 2016

15. Simulation Experiments
 Simulation using cylindrical arrays of microphones and
loudspeakers under free-field assumption
 Proposed method is compared with WFR filtering method
 Microphone array:
– Radius: 0.12 m, # of microphones: 32 in x 6 in
 Loudspeaker array:
– Radius: 1.5 m, # of loudspeakers: 32 in x 12 in
 Evaluation w/ signal-to-distortion ratio (SDR) at radius
July 19, 2016
[Koyama+ IEEE TASLP 2014]
Reproduced and original pressure distribution

16. Reproduced pressure distribution (x-y-plane)
July 19, 2016
PressureError
Proposed WFR
 Source location: (2.0 m, 155 deg, -0.4) m, Source signal: 1.6 kHz

17. Reproduced pressure distribution (y-z-plane)
July 19, 2016
PressureError
Proposed WFR
 Source location: (2.0 m, 155 deg, -0.4) m, Source signal: 1.6 kHz

18. Relationship between distance and SDR
July 19, 2016
 Source location: (2.0 m, 155 deg, -0.4) m, Source signal: 1.6 kHz
Almost the same reproduction
accuracy even when prior source
location was perturbed

19. Conclusion
 Source-location-informed sound field recording and
reproduction for several types of array geometries
– Signal conversion method that takes into account prior information on
primary source locations
– Spatial basis functions and their coefficients are optimized
– Two requirements:
1. Relationship between desired and received sound pressures can be
obtained
2. Amplitude distribution of driving signals of secondary sources can
be predicted from prior source locations
– Simulation results using cylindrical arrays indicated that region of high
reproduction accuracy of proposed method was larger than that of WFR
filtering method
July 19, 2016
Thank you for your attention!