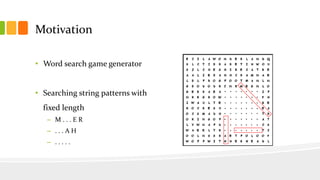
The document presents a fast exact string pattern-matching algorithm for fixed length patterns, designed to improve the efficiency of word search games. It details the motivation, problem definition, existing solutions, and the implemented algorithm, highlighting its dynamic in-memory data structure achieving approximately O(1) complexity. Testing results indicate the new algorithm is over 1300 times faster than naive methods, with varying memory consumption and initialization times based on list size settings.

1. Fast Exact String Pattern-Matching Algorithm for
Fixed Length Patterns
Ing. Ľuboš Takáč
PhD student
Faculty of Management Science and Informatics
University of Žilina

2. Presentation overview
• Motivation
• Problem Definition
• Existing Solutions
• Our Implemented Algorithm
• Testing Results
• Conclusion

3. Motivation
• Word search game generator
• Searching string patterns with
fixed length
– M . . . E R
– . . . A H
– . . . . .

4. Problem Definition
• Design fast in-memory data structure (class)
• Requirements
– fast searching, if it is possible with O(1) complexity
– each founded word get only once
– each founded word must be randomly chosen
– founded word have to match the pattern
class Model
FastStringPatternSearch
+ FastStringPatternSearch(String[], Random)
+ FastStringPatternSearch(String[])
+ reset() : void
+ searchPattern(String) : String

5. Existing Solutions
• Relational DB table with full-text index - access to hard drive
• Linked List or array in memory – O(N) complexity
• Indexing of array – necessary to index all possible combination of
patterns to have O(1) complexity
Number of
undefined
positions
0 1 2 3 4 5 6 7 8
Example of
pattern
PATTER
NS
PATT-
RNS
PA-TE-
NS
-AT--
RNS
P-T-E--S -A--ER-- --TT---- ----E--- --------
All combinations
count 1 8 28 56 70 56 28 8 1
Total combinations
count 256

6. Our Implemented Algorithm
• Dynamic in-memory tree(s) with linked list of words (id’s) on nodes
• Roots are in 3-dimensional matrix
• Nodes has 2-dimensional matrix of children

7. Root
• 3 dimensional matrix of root nodes with linked shuffled lists
– alphabet dimension
– word length dimension
– character position dimension
• Example
– We put the word “NAUTICAL” into nodes [N][8][1], [A][8][2], [U][8][3], …,
[L][8][8]
– When we search for pattern “. . U . . . . .”, we are looking into root node [U][8][3]
where we find word “NAUTICAL” in linked list

8. Root

9. Child nodes
• 2 dimensional matrix of child nodes with linked shuffled lists
– alphabet dimension
– word length dimension – can be determine from ancestor
– character position dimension

10. Searching algorithm
• Searching for pattern “. . T . E R . .”
1. Get the first defined character, pattern length and the position of first
defined character (T, 8, 3). Get a node of three-dimensional array data structure
at [character][length][position] ([T][8][3]). Continue to step 2 with this node.
2. If a node is null, string with this pattern does not exists. – END.
If a node is not null and a node has not children (leaf node) or pattern has no
further defined characters, find the first string in a node list which matches the
pattern. Return founded string or null if no string matches the pattern. – END.
If a node is not null and a node has children (not leaf node), take the next
defined character in pattern (E, position 5) and access two-dimensional array of
children nodes of node at element [position][character] ([5][E]), go to step 2
with the given node.

11. Complexity of algorithm
• We can set MaxListSize on leaf nodes, which determine the
complexity to O(L+MaxListSize), where L is the length of the string
• low MaxListSize = fast searching, high memory consumption,
slow initializing
• High MaxListSize = slow searching, low memory consumption,
fast initializing
• Recommendation
– Set it based on purpose, dictionary size
– Create data structure only once and share it

12. Other requirements
• Get every word only once
– Creating array map with boolean value “used” and comparing and updating it
– Function reset, which set all values to “not used” - O(N)
• Get randomly chosen words
– All linked list are shuffled after initialization
– After finding the word, we put the word on the end of linked list – O(1)
• Get words with pattern without character e.g. “. . . . . . .”
– Creating special linked lists with all sizes and put the words from dictionary there

13. Testing Results
• Dictionary with 225 thousands word
• Generating 5 000 word search games of size 25x25
• More than 1300 times faster than naive algorithm
We used for testing HP ProBook 6550b with configuration Win 7 Professional 64bit, Intel® Core ™ i5 CPU M450 2cores 2.40GHz, 4GB RAM, Java 7.
MaxListSize
Initializing
time (s)
Generating
time (s)
Memory
consumption
(MB)
Unlimited
1,508 989,643 86
5000
2,726 839,294 101
1000
4,843 400,539 265
500
7,062 324,728 340
100
16,141 279,410 808
Naive algorithm O(N) 0,095 381 073,600 15

14. Conclusion
• We design and implement fast in-memory data structure for searching
string patterns with fixed length
• Dynamic structure, up to O(1) complexity
• Randomly chosen words matching the pattern, each founded only
once
• Options to reset data structure, to get all words again without
initializing data structure ( complexity O(N) )

15. Thank you for your attention!
lubos.takac@gmail.com