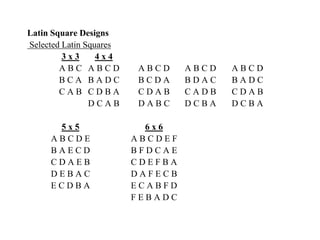
The document discusses the Graeco-Latin square design, defining Latin squares and their application in experimental studies to compare factors with controlled variables like rows and columns. It provides examples, including a courier company's evaluation of car brands over weeks using a Latin square design and a study on rat weight gain influenced by protein sources and levels. Additionally, it includes ANOVA tables for analysis, explaining statistical methods for assessing the results of experiments designed with Latin and Graeco-Latin squares.

1. Presentation
• Name: Nadeem Altaf
• Roll #: BSTF17E-122®
• Topic: Graeco Latin Square Design
• Present To: Mam Noureen Akhter

2. Latin Square Designs

3. Latin Square Designs
Selected Latin Squares
3 x 3 4 x 4
A B C A B C D A B C D A B C D A B C D
B C A B A D C B C D A B D A C B A D C
C A B C D B A C D A B C A D B C D A B
D C A B D A B C D C B A D C B A
5 x 5 6 x 6
A B C D E A B C D E F
B A E C D B F D C A E
C D A E B C D E F B A
D E B A C D A F E C B
E C D B A E C A B F D
F E B A D C

4. A Latin Square

5. Definition
• A Latin square is a square array of objects (letters A,
B, C, …) such that each object appears once and only
once in each row and each column. Example - 4 x 4
Latin Square.
A B C D
B C D A
C D A B
D A B C

6. In a Latin square You have three factors:
• Treatments (t) (letters A, B, C, …)
• Rows (t)
• Columns (t)
The number of treatments = the number of rows =
the number of colums = t.
The row-column treatments are represented by cells
in a t x t array.
The treatments are assigned to row-column
combinations using a Latin-square arrangement

7. Example
A courier company is interested in deciding
between five brands (D,P,F,C and R) of car
for its next purchase of fleet cars.
• The brands are all comparable in purchase price.
• The company wants to carry out a study that will
enable them to compare the brands with respect to
operating costs.
• For this purpose they select five drivers (Rows).
• In addition the study will be carried out over a
five week period (Columns = weeks).

8. • Each week a driver is assigned to a car using
randomization and a Latin Square Design.
• The average cost per mile is recorded at the end of
each week and is tabulated below:
Week
1 2 3 4 5
1 5.83 6.22 7.67 9.43 6.57
D P F C R
2 4.80 7.56 10.34 5.82 9.86
P D C R F
Drivers 3 7.43 11.29 7.01 10.48 9.27
F C R D P
4 6.60 9.54 11.11 10.84 15.05
R F D P C
5 11.24 6.34 11.30 12.58 16.04
C R P F D

9. The Model for a Latin Experiment
   
k
ij
j
i
k
k
ij
y 



 




i = 1,2,…, t j = 1,2,…, t
yij(k) = the observation in ith row and the jth
column receiving the kth treatment
 = overall mean
k = the effect of the ith treatment
i = the effect of the ith row
ij(k) = random error
k = 1,2,…, t
j = the effect of the jth column
No interaction
between rows,
columns and
treatments

10. • A Latin Square experiment is assumed to be a
three-factor experiment.
• The factors are rows, columns and treatments.
• It is assumed that there is no interaction between
rows, columns and treatments.
• The degrees of freedom for the interactions is
used to estimate error.

11. The Anova Table for a Latin Square Experiment
Source S.S. d.f. M.S. F p-value
Treat TSS t-1 MSTr MSTr /MSE
Rows RSS t-1 MSRow MSRow /MSE
Cols CSS t-1 MSCol MSCol /MSE
Error ESS (t-1)(t-2) MSE
Total SST t2 - 1

12. The Anova Table for Example
Source S.S. d.f. M.S. F p-value
Week 51.17887 4 12.79472 16.06 0.0001
Driver 69.44663 4 17.36166 21.79 0.0000
Car 70.90402 4 17.72601 22.24 0.0000
Error 9.56315 12 0.79693
Total 201.09267 24

13. Using SPSS for a Latin Square experiment
Rows Cols Trts Y

14. Select
Analyze->General Linear Model->Univariate

15. Select the dependent variable and
the three factors – Rows, Cols, Treats
Select Model

16. Identify a model that has only main
effects for Rows, Cols, Treats

17. Tests of Between-Subjects Effects
Dependent Variable: COST
191.530a
12 15.961 20.028 .000
2120.050 1 2120.050 2660.273 .000
69.447 4 17.362 21.786 .000
51.179 4 12.795 16.055 .000
70.904 4 17.726 22.243 .000
9.563 12 .797
2321.143 25
201.093 24
Source
Corrected Model
Intercept
DRIVER
WEEK
CAR
Error
Total
Corrected Total
Type III
Sum of
Squares df
Mean
Square F Sig.
R Squared = .952 (Adjusted R Squared = .905)
a.
The ANOVA table produced by SPSS

18. Example 2
In this Experiment we are again interested in how
weight gain (Y) in rats is affected by Source of
protein (Beef, Cereal, and Pork) and by Level of
Protein (High or Low).
There are a total of t = 3 X 2 = 6 treatment
combinations of the two factors.
• Beef -High Protein
• Cereal-High Protein
• Pork-High Protein
• Beef -Low Protein
• Cereal-Low Protein and
• Pork-Low Protein

19. In this example we will consider using a Latin Square
design
Six Initial Weight categories are identified for the
test animals in addition to Six Appetite categories.
• A test animal is then selected from each of the 6 X
6 = 36 combinations of Initial Weight and
Appetite categories.
• A Latin square is then used to assign the 6 diets to
the 36 test animals in the study.

20. In the latin square the letter
• A represents the high protein-cereal diet
• B represents the high protein-pork diet
• C represents the low protein-beef Diet
• D represents the low protein-cereal diet
• E represents the low protein-pork diet and
• F represents the high protein-beef diet.

21. The weight gain after a fixed period is measured for
each of the test animals and is tabulated below:
Appetite Category
1 2 3 4 5 6
1 62.1 84.3 61.5 66.3 73.0 104.7
A B C D E F
2 86.2 91.9 69.2 64.5 80.8 83.9
B F D C A E
Initial 3 63.9 71.1 69.6 90.4 100.7 93.2
Weight C D E F B A
Category 4 68.9 77.2 97.3 72.1 81.7 114.7
D A F E C B
5 73.8 73.3 78.6 101.9 111.5 95.3
E C A B F D
6 101.8 83.8 110.6 87.9 93.5 103.8
F E B A D C

22. The Anova Table for Example
Source S.S. d.f. M.S. F p-value
Inwt 1767.0836 5 353.41673 111.1 0.0000
App 2195.4331 5 439.08662 138.03 0.0000
Diet 4183.9132 5 836.78263 263.06 0.0000
Error 63.61999 20 3.181
Total 8210.0499 35

23. Diet SS partioned into main effects for Source and
Level of Protein
Source S.S. d.f. M.S. F p-value
Inwt 1767.0836 5 353.41673 111.1 0.0000
App 2195.4331 5 439.08662 138.03 0.0000
Source 631.22173 2 315.61087 99.22 0.0000
Level 2611.2097 1 2611.2097 820.88 0.0000
SL 941.48172 2 470.74086 147.99 0.0000
Error 63.61999 20 3.181
Total 8210.0499 35

24. Experimental Design
Of interest: to compare t treatments
(the treatment combinations of one or
several factors)

25. The Completely Randomized Design
Treats
1 2 3 … t
Experimental units randomly assigned to
treatments

26. The Model for a CR Experiment
ij
i
ij
y 

 


i = 1,2,…, t j = 1,2,…, n
yij = the observation in jth observation
receiving the ith treatment
 = overall mean
i = the effect of the ith
treatment
ij = random error

27. The Anova Table for a CR Experiment
Source S.S. d.f. M.S. F p-value
Treat SSTr t-1 MST MST /MSE
Error SSE t(n-1) MSE

28. Randomized Block Design
Blocks
All treats appear once in each block
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t
1
2
3
⁞
t

29. The Model for a RB Experiment
ij
j
i
ij
y 


 



i = 1,2,…, t j = 1,2,…, b
yij = the observation in jth block receiving the ith
treatment
 = overall mean
i = the effect of the ith treatment
ij = random error
j = the effect of the jth block
No interaction
between blocks
and treatments

30. • A Randomized Block experiment is
assumed to be a two-factor experiment.
• The factors are blocks and treatments.
• It is assumed that there is no interaction
between blocks and treatments.
• The degrees of freedom for the interaction is
used to estimate error.

31. The Anova Table for a randomized Block Experiment
Source S.S. d.f. M.S. F p-value
Treat SST t-1 MST MST /MSE
Block SSB n-1 MSB MSB /MSE
Error SSE (t-1)(b-1) MSE

32. The Latin square Design
All treats appear once in each row and
each column
Columns
Rows 1
2
3
⁞
t
2
3
t
1
1
3
2

33. The Model for a Latin Experiment
   
k
ij
j
i
k
k
ij
y 



 




i = 1,2,…, t j = 1,2,…, t
yij(k) = the observation in ith row and the jth
column receiving the kth treatment
 = overall mean
k = the effect of the ith treatment
i = the effect of the ith row
ij(k) = random error
k = 1,2,…, t
j = the effect of the jth column
No interaction
between rows,
columns and
treatments

34. • A Latin Square experiment is assumed to be a
three-factor experiment.
• The factors are rows, columns and treatments.
• It is assumed that there is no interaction between
rows, columns and treatments.
• The degrees of freedom for the interactions is
used to estimate error.

35. The Anova Table for a Latin Square Experiment
Source S.S. d.f. M.S. F p-value
Treat SSTr t-1 MSTr MSTr /MSE
Rows SSRow t-1 MSRow MSRow /MSE
Cols SSCol t-1 MSCol MSCol /MSE
Error SSE (t-1)(t-2) MSE
Total SST t2 - 1

36. Graeco-Latin Square Design
Mutually orthogonal Squares

37. Definition
A Graeco-Latin square consists of two latin squares (one
using the letters A, B, C, … the other using greek letters a, ,
c, …) such that when the two latin square are supper imposed
on each other the letters of one square appear once and only
once with the letters of the other square. The two Latin
squares are called mutually orthogonal.
Example: a 7 x 7 Graeco-Latin Square
Aa B C Df Ec F Gd
B Cf Dc E Fd Ga A
Cc D Ed Fa G A Bf
Dd Ea F G Af Bc C
E F Gf Ac B Cd Da
Ff Gc A Bd Ca D E
G Ad Ba C D Ef Fc

38. Note:
There exists at most (t –1) t x t Latin squares L1, L2,
…, Lt-1 such that any pair are mutually orthogonal.
e.g. It is possible that there exists a set of six 7 x 7
mutually orthogonal Latin squares L1, L2, L3, L4, L5,
L6 .

39. The Graeco-Latin Square Design - An Example
A researcher is interested in determining the effect of
two factors
• the percentage of Lysine in the diet and
• percentage of Protein in the diet
have on Milk Production in cows.
Previous similar experiments suggest that interaction
between the two factors is negligible.

40. For this reason it is decided to use a Greaco-Latin
square design to experimentally determine the two
effects of the two factors (Lysine and Protein).
Seven levels of each factor is selected
• 0.0(A), 0.1(B), 0.2(C), 0.3(D), 0.4(E), 0.5(F), and
0.6(G)% for Lysine and
• 2(a), 4(b), 6(c), 8(d), 10(e), 12(f) and 14(g)% for
Protein ).
• Seven animals (cows) are selected at random for
the experiment which is to be carried out over
seven three-month periods.

41. A Greaco-Latin Square is the used to assign the 7 X 7
combinations of levels of the two factors (Lysine and Protein)
to a period and a cow. The data is tabulated on below:
Period
1 2 3 4 5 6 7
1 304 436 350 504 417 519 432
(Aa (B (C (Df (Ec (F (Gd
2 381 505 425 564 494 350 413
  B (Cf (Dc (E (Fd (Ga (A
3 432 566 479 357 461 340 502
(Cc (D (Ed (Fa (G (A (Bf
Cows 4 442 372 536 366 495 425 507
(Dd (Ea (F (G (Af (Bc (C
5 496 449 493 345 509 481 380
(E (F (Gf (Ac (B (Cd (Da
6 534 421 452 427 346 478 397
(Ff (Gc (A (Bd (Ca (D (E
7 543 386 435 485 406 554 410
(G (Ad (Ba (C (D (Ef (Fc

42. The Model for a Graeco-Latin Experiment
   
kl
ij
j
i
l
k
kl
ij
y 




 





i = 1,2,…, t j = 1,2,…, t
yij(kl) = the observation in ith row and the jth
column receiving the kth Latin treatment
and the lth Greek treatment
k = 1,2,…, t l = 1,2,…, t

43.  = overall mean
k = the effect of the kth Latin treatment
i = the effect of the ith row
ij(k) = random error
j = the effect of the jth column
No interaction between rows, columns,
Latin treatments and Greek treatments
l = the effect of the lth Greek treatment

44. • A Graeco-Latin Square experiment is assumed to
be a four-factor experiment.
• The factors are rows, columns, Latin treatments
and Greek treatments.
• It is assumed that there is no interaction between
rows, columns, Latin treatments and Greek
treatments.
• The degrees of freedom for the interactions is
used to estimate error.

45. The Anova Table for a
Greaco-Latin Square Experiment
Source S.S. d.f. M.S. F p-value
Latin SSLa t-1 MSLa MSLa /MSE
Greek SSGr t-1 MSGr MSGr /MSE
Rows SSRow t-1 MSRow MSRow /MSE
Cols SSCol t-1 MSCol MSCol /MSE
Error SSE (t-1)(t-3) MSE
Total SST t2 - 1

46. The Anova Table for Example
Source S.S. d.f. M.S. F p-value
Protein 160242.82 6 26707.1361 41.23 0.0000
Lysine 30718.24 6 5119.70748 7.9 0.0001
Cow 2124.24 6 354.04082 0.55 0.7676
Period 5831.96 6 971.9932 1.5 0.2204
Error 15544.41 24 647.68367
Total 214461.67 48

47. Next topic: Incomplete Block
designs