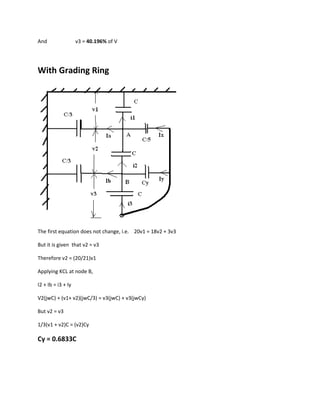
The document describes a 3 unit capacitor system where: 1) Each unit has a capacitance C and the capacitance from each unit to ground and between connectors is C/3 and C/5 respectively. 2) Calculations show the voltage across each unit is 31.5%, 28.3%, and 40.196% of the total voltage respectively. 3) To make the voltage across the bottom unit equal to that of the next unit, the capacitance between the bottom connector and line must be increased to 0.6833C by a guard ring.

1. 1. In a string of three insulator units, the capacitance of each unit is C, from each conductor to
ground is C/3, and from each connector to the line conductor is C/5. Calculate the voltage across
each unit as a % of the total voltage. To what value the capacitance between the connector of
the bottom unit and the line has to be increased by a guard ring to make the voltage across it
equal to that across the next higher unit? [31.5%, 28.3%, 40.196%; 0.6833C]
Solution:
Apply KCL at node A
I1+Ia = i2 + Ix
V1(jwC) + v1(jwC/3) = v2(jwC) + (v2+v3)(jwC/5)
20v1 = 18v2 + 3v3 ………(1)
Apply KCL at node B
i2 + Ib = I3 + Iy
20v2 +5v1 = 18v3 ………(2)
Eliminating v3 from the above 2 equations
V2 = 115/128 v1
And , then v3 = 1.276 v1
Hence, v1 + v2 + v3 = V or v1 = 1/3.174 V = 31.5% of V
Similarly, v2 = 28.3% of V

2. And v3 = 40.196% of V
With Grading Ring
The first equation does not change, i.e. 20v1 = 18v2 + 3v3
But it is given that v2 = v3
Therefore v2 = (20/21)v1
Applying KCL at node B,
I2 + Ib = i3 + Iy
V2(jwC) + (v1+ v2)(jwC/3) = v3(jwC) + v3(jwCy)
But v2 = v3
1/3(v1 + v2)C = (v2)Cy
Cy = 0.6833C