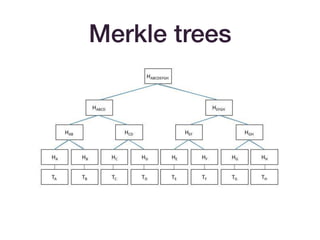
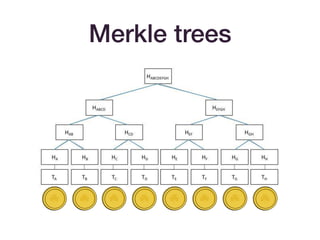
The document discusses advancements in hash functions specifically for SNARKs (Succinct Non-interactive Arguments of Knowledge), highlighting their importance in cryptographic protocols. It covers various hash functions and methods for achieving efficiency and security, including SHA2, Merkle trees, Pedersen hashes, and specific elliptic curve hashing techniques. The document emphasizes the need for low arithmetic complexity while maintaining security properties, providing a roadmap for selecting suitable hash functions in SNARK applications.

1. snarks <3 hash
functions
Rebekah Mercer
O(1) Labs

2. Roadmap
• The state of the art for arithmetic circuit-friendly hash
functions.
• What do we need to keep in mind when choosing hash
functions for use inside snarks?
• Which hash functions best satisfy these requirements?

3. Using SHA2

4. Using SHA2
• Lack of algebraic structure
• Working with bytes and words is nice and fast in normal
software but doesn’t quite translate to speed in snarks

5. Using SHA2
• SHA2 has 27,446 constraints for a 512 bit message, and
proof creation takes ~1.5 seconds.
• This means 53.6 constraints per bit processed.

6. Commitments
• Commitments only require second pre-image resistance,
or potentially collision resistance.
• Constructing a low arithmetic complexity hash function
that achieves only collision resistance might be simpler!

7. Merkle trees

8. Merkle trees

9. Pedersen
• Windowing: hardcoding parameters and using lookups
(which are cheaper) to replace exponentiations.
• Leads to around 1.7 constraints per bit processed.
~896 constraints to hash a 512-bit message.
• Provable security from DL assumption.
With n generators Gi, and message m made of bits mi, we
compute:
m1G1 + m2G2 + … + mnGn

10. Indifferentiability from a
random oracle
• Schnorr signatures: using the Fiat-Shamir transform
requires the hash function to be modelled as a random
oracle.
• Proof composition with universal-setup SNARKs (these
often use the Fiat-Shamir transform to make the protocols
non-interactive without relying on heavier cryptographic
machinery).

11. RO hashing to bitstrings
• To replace SHA with its full functionality, various hash
functions (or pairs of hash functions) have been recently
suggested:
• MPC-inspired low-complexity hash functions:
• [AGRRT16] : MIMChash
• [GRRSS16], [AGP+19] : symmetric key
primitives for low arithmetic circuit complexity

12. RO hashing to bitstrings
• To replace SHA with its full functionality, various hash
functions (or pairs of hash functions) have been recently
suggested:
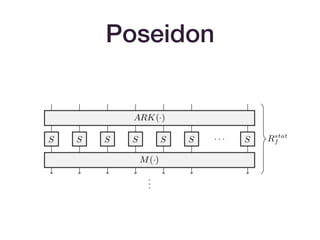
• HADESMIMC-inspired hash functions:
• [AABDS19] : Vision/Rescue
• [GKK+19] : STARKAD/POSEIDON

13. Poseidon

14. Poseidon
• Combines full rounds and
partial rounds to increase
efficiency.
• Operations are defined to
occur in the field, so have
low arithmetic circuit
complexity.
• Gives 228 constraints in
MNT4/6’s case, so 0.3
constraints per bit
processed.

15. S-box structure
• Poseidon uses xα as its s-box, with α = 3 if x3 is a bijection
(which happens only if r != 3k + 1, which leaves only
r = 2 mod 3).
• It otherwise recommends 1/α, but you can also choose α
as any prime with r != αk + 1 (i.e. α doesn’t divide r - 1)
• We choose α = 11.

16. • Rescue uses both xα and x1/α as s-boxes. These give the
same complexity in terms of constraints, but x1/α is slow
to compute outside of the snark.
• Poseidon also uses partial rounds, removing a lot of
constraints due to invocations of the s-box itself.
• A more thorough comparison coming soon!
S-box structure

17. Indifferentiable hashing to
elliptic curves: motivation
• Verifiable random functions (VRFs)
• Password authenticated key exchange (PAKE)
• BLS signatures

18. • Proof of stake protocols can rely on the existence of a
VRF, and the most efficient of these uses a hash function
H’ that maps a message into an elliptic curve point H’(m).
• A proposer wins the right to propose a block if, for
(hx, hy) = sk H’(m), hx > target value.
• Can provide a proof as before, with base H(‘m) instead of
base g.
Verifiable random functions

19. • Proof of stake protocols can rely on the existence of a
VRF, and the most efficient of these uses a hash function
H’ that maps a message into an elliptic curve point H’(m).
• A proposer wins the right to propose a block if, for
(hx, hy) = sk H’(m), hx > target value.
• Can provide a proof as before, with base H(‘m) instead of
base g.
Verifiable random functions

20. • Proof of stake protocols can rely on the existence of a
VRF, and the most efficient of these uses a hash function
H’ that maps a message into an elliptic curve point H’(m).
• A proposer wins the right to propose a block if, for
(hx, hy) = sk H’(m), hx > target value.
• The proof looks just like Schnorr, but with base H’(m)
instead of base g.
Verifiable random functions

21. r 𝔽q
R = (rx, ry) = rH’(m)
z = cx + r
Verifiable random functions
rx, z Compute c,
compute R,
verify
zH’(m) = ch + R
c = H(R, H’(m), h)
H’, m, hx, H’(m), h = H’(m)x

22. r 𝔽q
R = (rx, ry) = rH’(m)
z = cx + r
Verifiable random functions
rx, z Compute c,
compute R,
verify
zH’(m) = ch + R
c = H(R, H’(m), h)
H’, m, hx, H’(m), h = H’(m)x

23. Snarks with private input
• Simulation extractability
• Ensures that if you can produce a valid transaction, then a
valid witness can be extracted.
• [BG18] transforms Groth16 into a simulation extractable
SNARK.
• It achieves this by including a message hashed to an
elliptic curve point alongside the proof.

24. snark-friendly hashing
to elliptic curves

25. Embedded curves
With 𝔾 = E(𝔽q), (x, y) ∈ 𝔾 means (x, y) ∈ 𝔽q × 𝔽q
Arithmetic inside the snark happens in 𝔽r.
So what if we can define a curve with (x, y) ∈ 𝔽r × 𝔽r?
Then we would be able to do elliptic curve arithmetic inside
a snark! efficiently!
A curve built with coordinates and a group operation defined
in 𝔽r for this reason is referred to as an embedded curve.

26. Try and increment

27. Try and increment
Finding whether or not f(x) is a quadratic residue takes an
exponentiation.
Square rooting (if f(x) is in QR), can be done via methods
with very different efficiency depending on your prime.

28. Try and increment
Approximately half of x ∈ 𝔽r give f(x) ∈ QR.
k is a parameter set so that the probability of the algorithm
terminating without giving an answer, assuming the QRs are
well distributed throughout 𝔽r, is 1/2k.
But setting k to a reasonable parameter leads to huge circuits.

29. h(m)G: BLS signatures
• pk = xG, s = xH(m), verification is e(H(m), pk) = e(s, G).
• With H(m) = h(m)G, we can produce s = xH(m) as h(m)pk
and forge a signature for any m and pk.
• Constraints = costRO + exponentiation (228 * log(r) * 2)
s = xH(m)

30. Icart-style encodings
• These maps look like H = f(h(u)).
• The basic map of [Icart09] achieves one-wayness (if h is
one-way).
• The extension in [BCI+10] to f(h(m)) + gh(m) achieves
indistinguishability from a random oracle, assuming that
h(m) achieves this. (Think of gh(m) as a one-time pad.)

31. Icart-style encodings
• These maps look like H = f(h(u)).
• The basic map of [Icart09] achieves one-wayness (if h is
one-way).
• The extension in [BCI+10] to f(h(m)) + gh(m) achieves
indistinguishability from a random oracle, assuming that
h(m) achieves this. (Think of gh(m) as a one-time pad.)

32. Icart-style encodings
• The basic function of [Icart09] achieves one-wayness (if h
is one-way).
• The extension in [BCI+10] to f(h0(u)) + f(h1(u)) achieves
indifferentiability from a random oracle, assuming that
h0(u) and h1(u) achieve this. (Think of f(h1(u)) as a one-time
pad.)
• Assumes p = 2 mod 3.

33. Icart-style encodings
• The basic function of [Icart09] achieves one-wayness (if h
is one-way).
• The extension in [BCI+10] to f(h0(u)) + f(h1(u)) achieves
indifferentiability from a random oracle, assuming that
h0(u) and h1(u) achieve this. (Think of f(h1(u)) as a one-time
pad.)
• Assumes p = 2 mod 3.

34. Icart-style encodings
• The basic function of [Icart09] achieves one-wayness (if h
is one-way).
• The extension in [BCI+10] to f(h0(u)) + f(h1(u)) achieves
indifferentiability from a random oracle, assuming that
h0(u) and h1(u) achieve this. (Think of f(h1(u)) as a one-time
pad.)
• Assumes r = 2 mod 3.

35. Skałba/SWU-style encodings
• The map has the form, with g the curve equation,
g(x1) g(x2) g(x3) = u2
which guarantees that one of g(x1), g(x2), or g(x3) is a
square, and so in QR, and so we can use it to construct a
point (x, y) ∈ E(𝔽r).

36. Skałba/SWU-style encodings
From [BCIMRT10]

37. • [BCI+10] extends and simplifies the SWU encoding,
moving it from just achieving one-wayness to also
achieving indifferentiability from a random oracle, but only
with r = 3 mod 4.
• [WB19] then removes this restriction and generalises,
proposing a construction for ab != 0, and one that works
even in this case.
Skałba/SWU-style encodings

38. What’s special about
hashing inside snarks?
• Randomised functions!
• We can make the computations faster if we can verify,
rather than compute, the hash function inside of the
snark.
• Imagine, rather than performing a square root of α with
Tonelli-Shanks, we instead give the square root of α,
called x, as input, and the snark circuit checks x*x = α.
• This takes us from O((log r)3) run time to O(1).

39. • t = hRO(m)
• We have f(x1(t)), … f(x3(t)), and pick the first square.
• Checking squareness outside of snark: exponentiation.
• Checking squareness inside of snark: the formula is
simple, but is an exponentiation, so requires O(log r)
constraints.
Simplifying WB19 for snarks

40. • Precompute β ∈ NQR. (This is hardcoded.)
• Then either:
• If a ∈ QR, there exists x with x2 = a mod r, so submit x.
• Or if a ∈ NQR, sqrt(aβ) exists — for any a ∈ NQR, β ∈ NQR,
we have that aβ ∈ QR. Then submit x with x2 = aβ mod r.
• Then we have:
x, b = witness,
assert xx = ba + (1 - b) aβ,
return b
Proving a ∈ QR or a ∈ NQR

41. Summary
• Hashing to elliptic curves inside snarks is a little different!
We need deterministic time algorithms that are finite field
friendly.
• Functions for hashing to elliptic curves are already fairly
finite field friendly!
• Depending on the curve equation of the embedded curve,
there are different algorithms with different efficiencies for
you to use.
• snarks <3 hash functions

42. Thanks!
• Hashing with collision resistance/
second preimage resistance: use
Pedersen hashes (fun details here:
https://github.com/zcash/zcash/
issues/2234)
• Hashing with indifferentiability
from a RO: use Poseidon
• Hashing to an elliptic curve with
indifferentiability from a RO: use
WB19
• snarks <3 hash functions

43. RO hashes
[AGRRT16] : M. Albrecht, L. Grassi, C. Rechberger, A. Roy, and T. Tiessen. MiMC:
Efficient encryption and cryptographic hashing with minimal multiplicative complexity.
https://eprint.iacr.org/2016/492
[GRRSS16] : L. Grassi, C. Rechberger, D. Rotaru, P. Scholl, and N. P. Smart. MPC-
Friendly Symmetric Key Primitives. https://eprint.iacr.org/2016/542
[AGP+19] : M. R. Albrecht, L. Grassi, L. Perrin, S. Ramacher, C. Rechberger, D. Rotaru,
A. Roy, and M. Schofnegger. Feistel Structures for MPC, and More. https://
eprint.iacr.org/2019/397
[AABDS19] : A. Aly, T. Ashur, E. Ben-Sasson, S. Dhooghe, and A. Szepieniec. Design
of Symmetric-Key Primitives for Advanced Cryptographic Protocols. https://
eprint.iacr.org/2019/426
[GKK+19] : L. Grassi, D. Kales, D. Khovratovich, A.Roy, C. Rechberger, and M.
Schofnegger. Starkad and Poseidon: New Hash Functions for Zero Knowledge Proof
Systems. https://eprint.iacr.org/2019/458

44. RO hashes to elliptic curves
[SvdW06] A. Shallue and C. van de Woestijne. Construction of rational points on
elliptic curves over finite fields.
[Ulas07] M. Ulas. Rational points on certain hyperelliptic curves over finite fields.
https://arxiv.org/pdf/0706.1448.pdf
[Icart09] T. Icart. How to Hash into Elliptic Curves. https://eprint.iacr.org/2009/226
[BCI+10] E. Brier, J. Coron, T. Icart, D. Madore, H. Randriam, and M. Tibouchi.
Efficient Indifferentiable Hashing into Ordinary Elliptic Curves. https://eprint.iacr.org/
2009/340
[BHKL13] D. J. Bernstein, M. Hamburg, A. Krasnova, and T. Lange. Elligator. https://
elligator.cr.yp.to
[WB19] R. S. Wahby and D. Boneh. Fast and simple constant-time hashing to the
BLS12-381 elliptic curve. https://eprint.iacr.org/2019/403