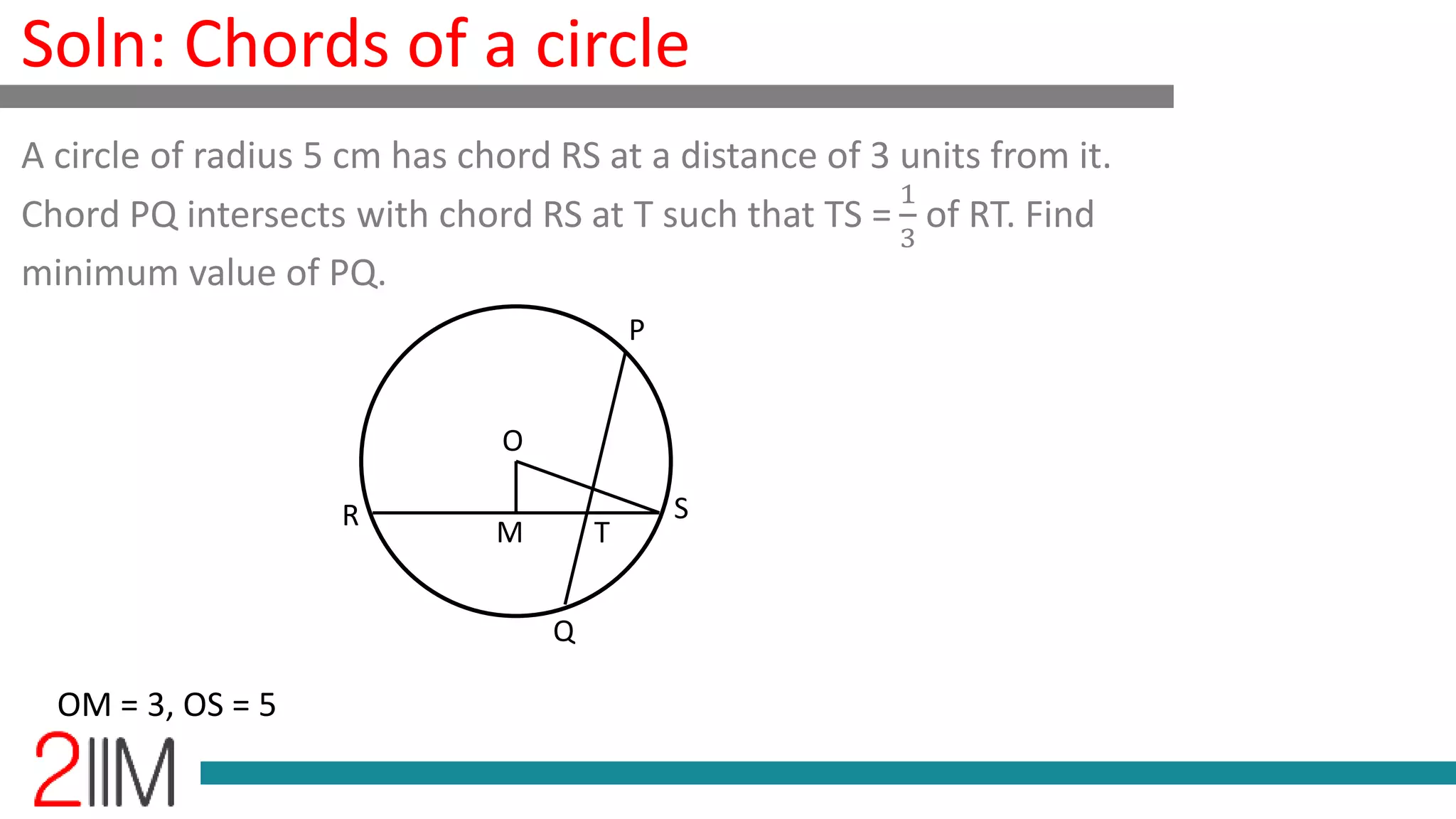
The document discusses the geometry problem of finding the minimum value of chord pq in a circle with a radius of 5 cm, where chord rs is at a distance of 3 units from the center and intersects with chord pq at point t. It uses the Pythagorean theorem and the intersecting chords theorem to establish relationships between the segments of the chords. The minimum value found for pq is 4√3, which corresponds to answer choice (b).

1. Geometry Q18

2. Qn: Chords of a circle
(a) 63 (b) 43
(c) 83 (d) 23
A circle of radius 5 cm has chord RS at a distance of 3 units from it.
Chord PQ intersects with chord RS at T such that TS =
1
3
of RT. Find
minimum value of PQ.

3. Soln: Chords of a circle
OM = 3, OS = 5
A circle of radius 5 cm has chord RS at a distance of 3 units from it.
Chord PQ intersects with chord RS at T such that TS =
1
3
of RT. Find
minimum value of PQ.
P
Q
O
T
SR
M

4. Soln: Chords of a circle
MS = 4 = RM {Using Pythagoras theorem}
 RS = 8 cms
TS =
1
3
of RT
TS =
1
4
of RS
If RS = 8 cms
TS = 2 cms
A circle of radius 5 cm has chord RS at a distance of 3 units from it.
Chord PQ intersects with chord RS at T such that TS =
1
3
of RT. Find
minimum value of PQ.

5. Soln: Chords of a circle
RT × TS = PT × TQ
{Intersecting Chords theorem: When there are two intersecting chords, the
product of the rectangle formed by the segments of one chord is equal to
the product of the rectangle formed by the segments of the other.}
6 × 2 = PT × TQ
PT × TQ = 12
By AM – GM inequality,
PT+TQ
2
≥ PT x TQ
A circle of radius 5 cm has chord RS at a distance of 3 units from it.
Chord PQ intersects with chord RS at T such that TS =
1
3
of RT. Find
minimum value of PQ.

6. Soln: Chords of a circle
PT+TQ
2
≥ 12
PT + TQ ≥ 212
 PQ ≥ 212
Or PQ ≥ 43
Minimum PQ = 43
Answer choice (b)
A circle of radius 5 cm has chord RS at a distance of 3 units from it.
Chord PQ intersects with chord RS at T such that TS =
1
3
of RT. Find
minimum value of PQ.