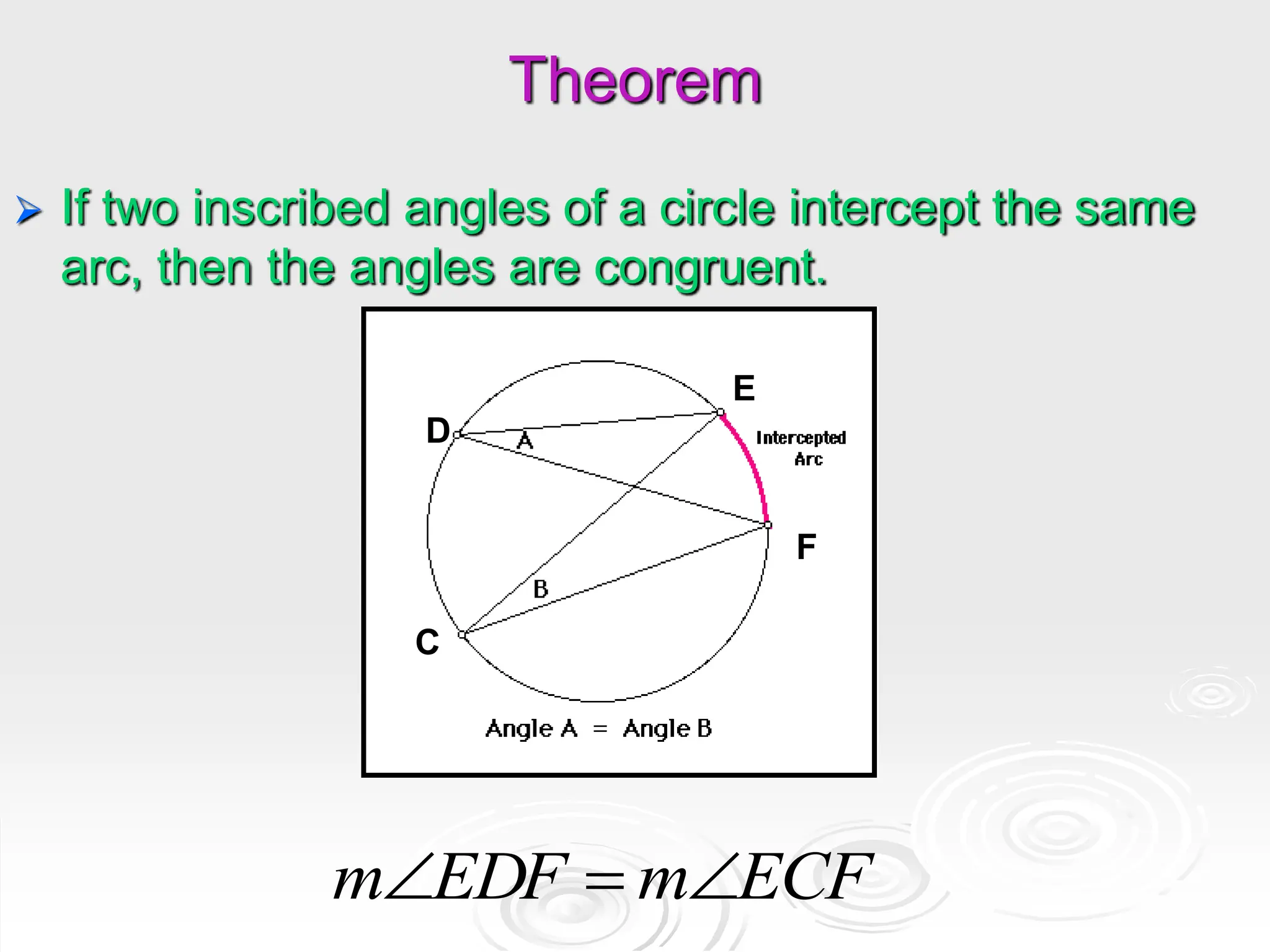
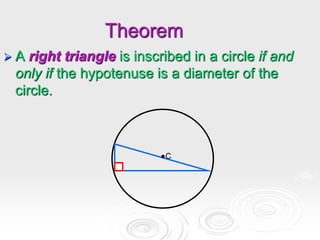
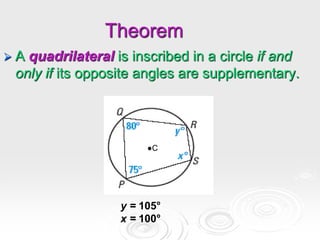
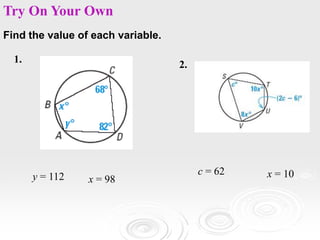
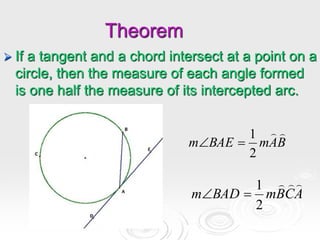
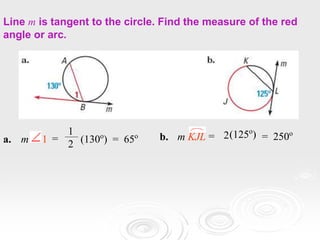
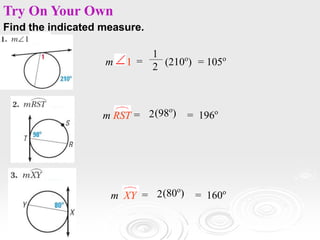
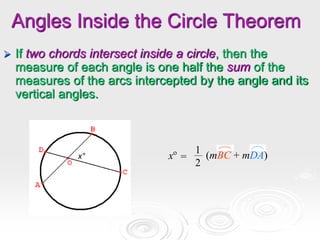
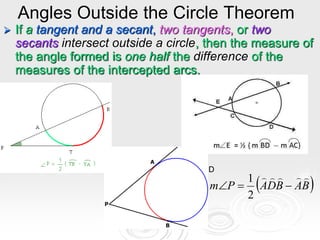
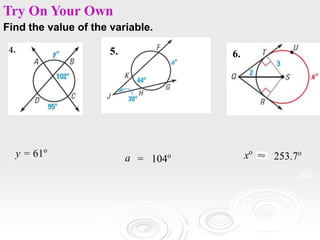
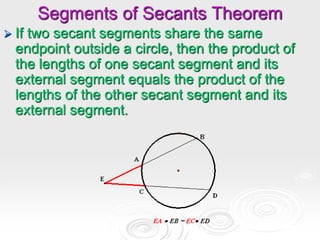
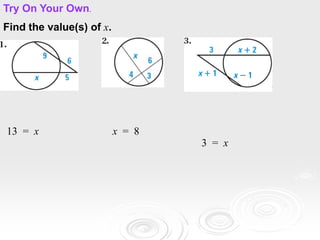
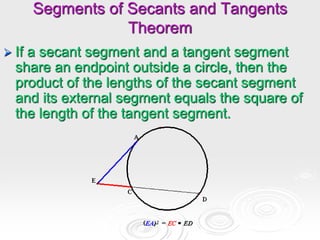
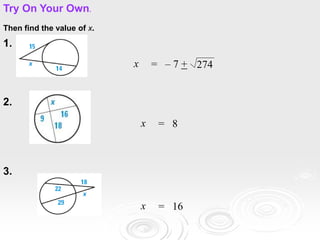
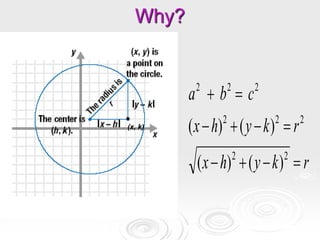
The document provides information about properties of circles, including theorems about angles formed by chords, secants, and tangents intersecting inside and outside circles, as well as theorems about relationships between lengths of segments of chords and secants. It also discusses writing equations of circles in standard form given the center and radius, finding the center and radius from a standard equation, and graphing circles from standard equations. Examples are provided to demonstrate applying the theorems and writing/graphing circle equations.

1. Theorem
 If two inscribed angles of a circle intercept the same
arc, then the angles are congruent.
ECF
m
EDF
m 


F
E
D
C

2. Find the measure of the red arc or angle.
1.
m G = mHF = (90o
) = 45o
1
2
1
2
Try On Your Own
2. mTV = 2m U = 2 38o
= 76o
.
3.
ZYN ZXN
ZXN 72°

3. Inscribed Polygons
 A polygon is inscribed if all of its vertices lie on
a circle.
 Circle containing the vertices is a Circumscribed
Circle.

4. Theorem
 A right triangle is inscribed in a circle if and
only if the hypotenuse is a diameter of the
circle.
●C

5. Theorem
 A quadrilateral is inscribed in a circle if and
only if its opposite angles are supplementary.
●C
y = 105°
x = 100°

6. 1.
Find the value of each variable.
y = 112 x = 98
2.
c = 62 x = 10
Try On Your Own

7. Theorem
 If a tangent and a chord intersect at a point on a
circle, then the measure of each angle formed
is one half the measure of its intercepted arc.
B
A
m
BAE
m


2
1


A
C
B
m
BAD
m



2
1



8. Line m is tangent to the circle. Find the measure of the red
angle or arc.
=
1
2 (130o
) = 65o = 2(125o
) = 250o
b. m KJL
a. m 1

9. Find the indicated measure.
=
1
2 (210o
) = 105o
m 1
Try On Your Own
= 2(98o
) = 196o
m RST
= 2(80o
) = 160o
m XY

10. Angles Inside the Circle Theorem
 If two chords intersect inside a circle, then the
measure of each angle is one half the sum of the
measures of the arcs intercepted by the angle and its
vertical angles.
xo
=
1
2
(mBC + mDA)
x°

11. Find the value of x.
The chords JL and KM intersect inside
the circle.
Use Theorem 10.12.
xo
=
1
2
(mJM + mLK)
xo
=
1
2
(130o
+ 156o
) Substitute.
xo
= 143 Simplify.

12. Angles Outside the Circle Theorem
 If a tangent and a secant, two tangents, or two
secants intersect outside a circle, then the measure of
the angle formed is one half the difference of the
measures of the intercepted arcs.
 
B
A
B
D
A
P
m








2
1
D

13. Find the value of x.
Use Theorem 10.13.
Substitute.
Simplify.
The tangent CD and the secant CB
intersect outside the circle.
=
1
2
(178o
– 76o
)
xo
= 51
x
m BCD (mAD – mBD)
=
1
2

14. Find the value of the variable.
y = 61o
Try On Your Own
= 104o
a
5.
xo
253.7o
6.

15. Segments of the Chords
 If two chords intersect in the interior of the
circle, then the product of the lengths of the
segments of one chord is equal to the product
of the lengths of the segments of the other
chord.

16. EXAMPLE 1
Find ML and JK.
NK NJ = NL NM Use Theorem
x (x + 4) = (x + 1) (x + 2) Substitute.
x2
+ 4x = x2
+ 3x + 2 Simplify.
4x = 3x + 2 Subtract x2
from each side.
x = 2 Solve for x.
ML = ( x + 2 ) + ( x + 1)
= 2 + 2 + 2 + 1
= 7
JK = x + ( x + 4)
= 2 + 2 + 4
= 8

17. Segments of Secants Theorem
 If two secant segments share the same
endpoint outside a circle, then the product of
the lengths of one secant segment and its
external segment equals the product of the
lengths of the other secant segment and its
external segment.

18. RQ RP = RS RT Use Theorem 10.15.
4 (5 + 4) = 3 (x + 3) Substitute.
36 = 3x + 9 Simplify.
9 = x Solve for x
The correct answer is D.
Find x.

19. Find the value(s) of x.
13 = x
Try On Your Own.
x = 8
3 = x

20. Segments of Secants and Tangents
Theorem
 If a secant segment and a tangent segment
share an endpoint outside a circle, then the
product of the lengths of the secant segment
and its external segment equals the square of
the length of the tangent segment.

21. Use the figure at the right to find RS.
256 = x2
+ 8x
0 = x2 + 8x – 256
RQ2
= RS RT
162
= x (x + 8)
x –8 + 82
– 4(1) (– 256)
2(1)
=
x = – 4 + 4 17
Use Theorem.
Substitute.
Simplify.
Write in standard form.
Use quadratic formula.
Simplify.
= – 4 + 4 17
So, x 12.49, and RS 12.49

22. Find the value of x.
1.
x = 2
Try On Your Own.
2.
x =
24
5
3.
x = 8

23. 1.
Try On Your Own.
2.
3.
Then find the value of x.
x = – 7 + 274
x = 8
x = 16

24. Chapter 10 Properties of Circles
Date:
Aim: 10.7: Write and Graph Equations of Circles
Do Now: Take out Homework from Tuesday
night.
Find the value of x for the problems below.
1.
x = 2
2.
x = 24
5

25. Standard Equation of a Circle
    2
2
2
r
k
y
h
x 




26. Why?
●
(x, k)
r
k
y
h
x
r
k
y
h
x
c
b
a










2
2
2
2
2
2
2
2
)
(
)
(
)
(
)
(

27. Write the equation of the circle shown.
The radius is 3 and the center is at the origin.
x2
+ y2
= r2
x2
+ y2
= 32
x2
+ y2
= 9
Equation of circle
Substitute.
Simplify.
The equation of the circle is x2
+ y2
= 9

28. Write the standard equation of a circle with center (0, –9) and
radius 4.2.
(x – h)2
+ ( y – k)2
= r2
(x – 0)2
+ ( y – (–9))2
= 4.22
x2
+ ( y + 9)2
= 17.64
Standard equation of a circle
Substitute.
Simplify.
C ●
(0, -9)
4.2

29. Write the standard equation of the circle with the given
center and radius.
1. Center (0, 0), radius 2.5
x2
+ y2
= 6.25
Try On Your Own.
2. Center (–2, 5), radius 7
(x + 2)2
+ ( y – 5)2
= 49

30. EXAMPLE 3
The point (–5, 6) is on a circle with center (–1, 3). Write the
standard equation of the circle.
r = [–5 – (–1)]2
+ (6 – 3)2
= (–4)2
+ 32
= 5
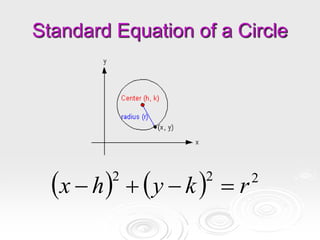
Substitute (h, k) = (–1, 3) and r = 5 into the equation of the circle.
(x – h)2
+ (y – k)2
= r2
[x – (–1)]2
+ (y – 3)2
= 52
(x +1)2
+ (y – 3)2
= 25
(x +1)2
+ (y – 3)2
= 25.
Steps:
1. Find values of h, k, and r by using the distance
formula.
2. Substitute your values into the equation for a
circle.
   2
1
2
2
1
2 y
y
x
x
d 




31. 1. The point (3, 4) is on a circle whose center is (1, 4). Write the
standard equation of the circle.
The standard equation of the circle is
(x – 1)2
+ (y – 4)2
= 4.
Try On Your Own.
2. The point (–1 , 2) is on a circle whose center is (2, 6).
Write the standard equation of the circle.
The standard equation of the circle is
(x – 2)2
+ (y – 6)2
= 25.

32. Graph A Circle
The equation of a circle is (x – 4)2
+ (y + 2)2
= 36.
GRAPH
Rewrite the equation to find the center
and radius.
(x – 4)2
+ (y +2)2
= 36
(x – 4)2
+ [y – (–2)]2
= 62
The center is (4, –2) and the radius is 6.

33. 1. The equation of a circle is (x – 4)2 + (y + 3)2 = 16.
Graph the circle.
Try On Your Own.
6. The equation of a circle is (x + 8)2 + (y + 5)2 = 121.
Graph the circle.