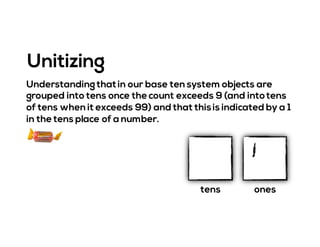
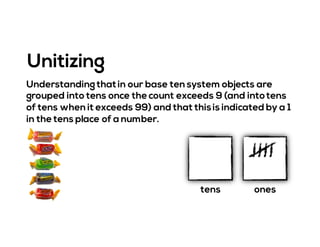
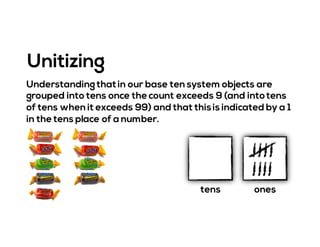
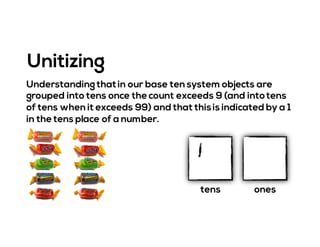
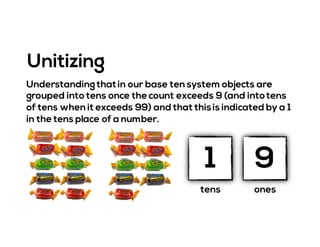
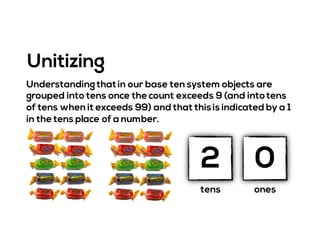
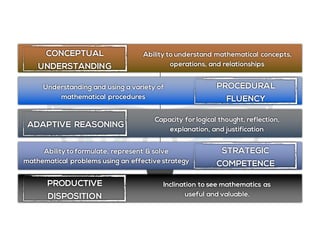
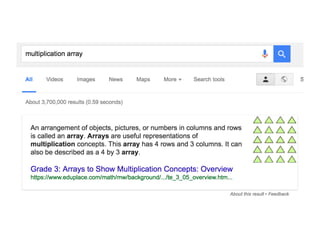
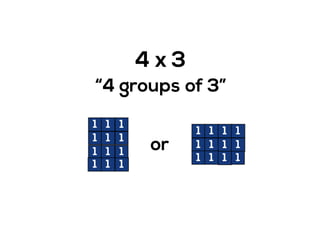
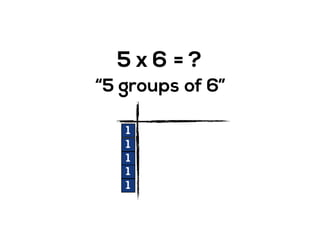
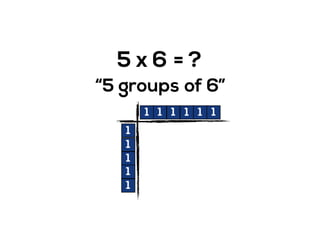
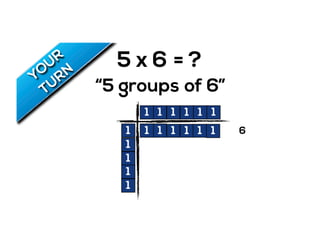
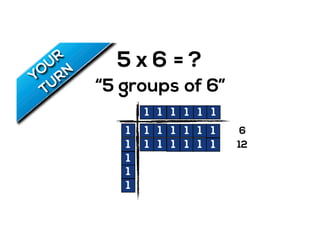
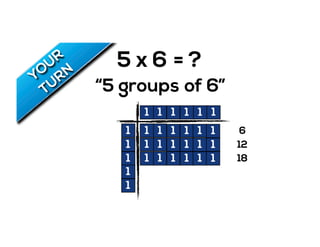
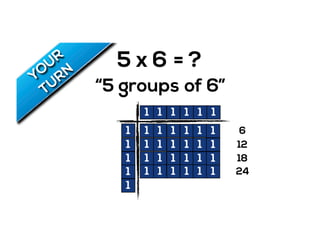
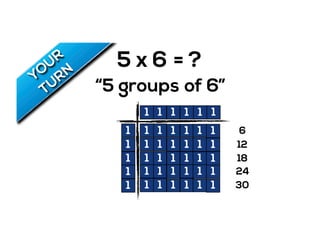
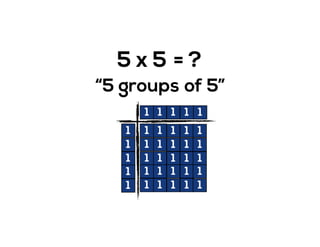
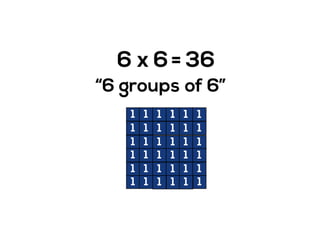
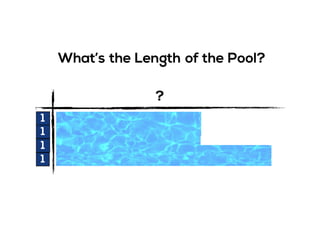
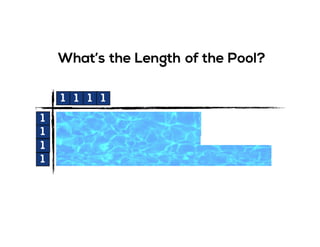
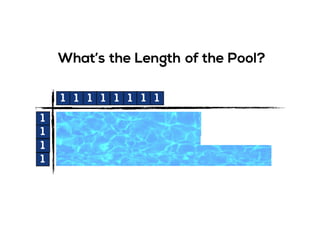
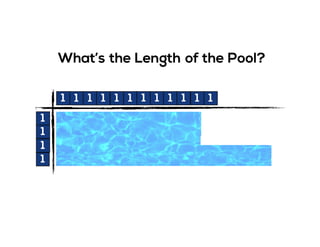
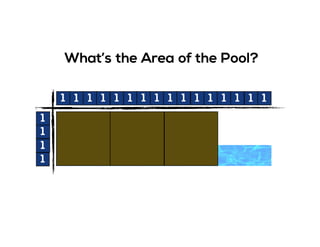
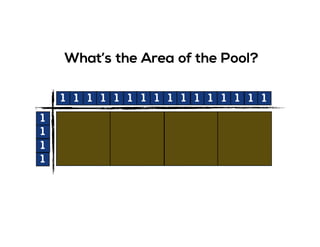
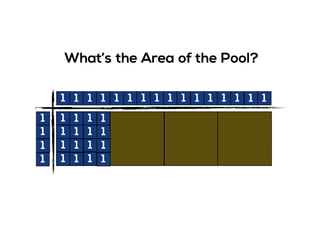
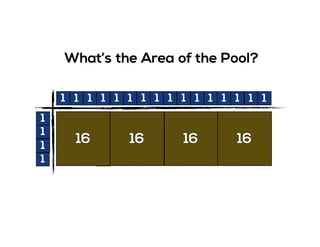
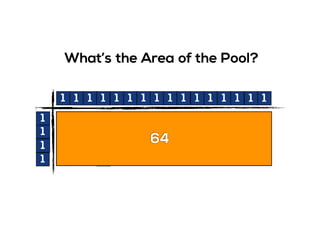
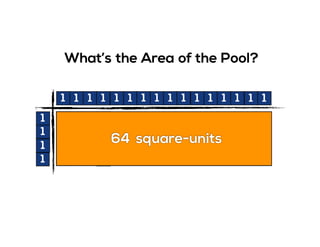
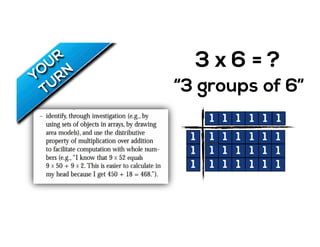
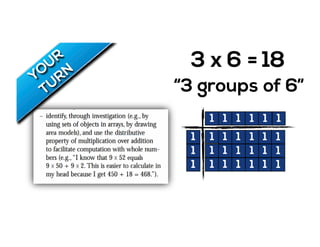
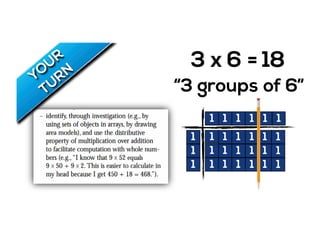
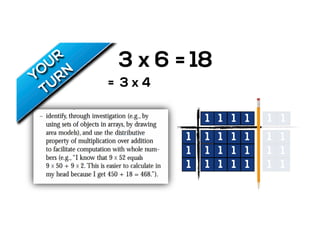
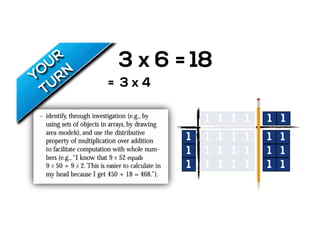
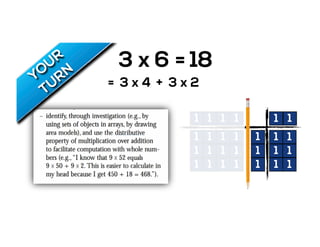
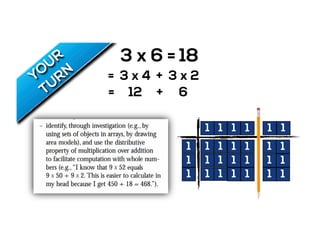
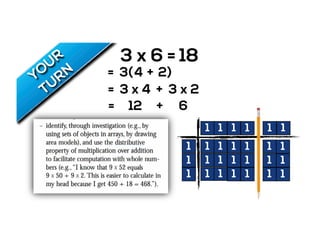
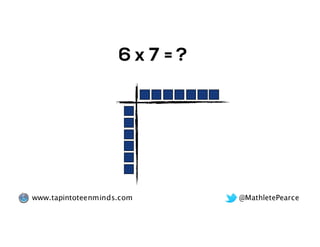
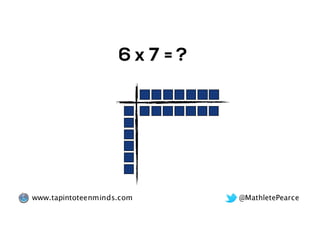
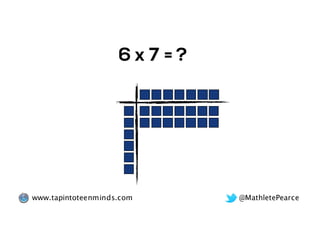
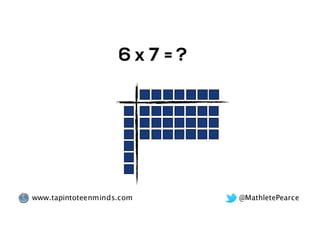
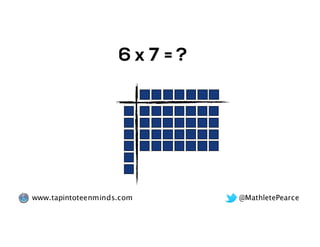
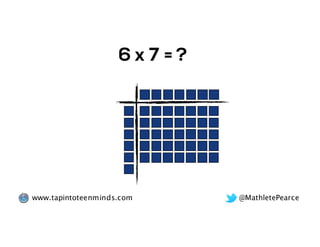
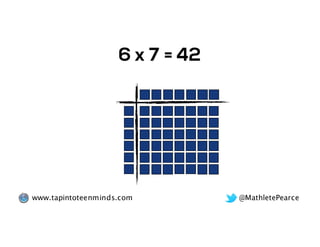
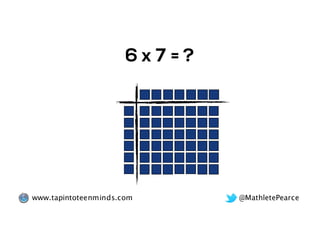
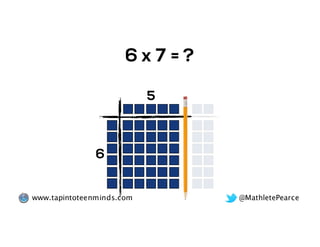
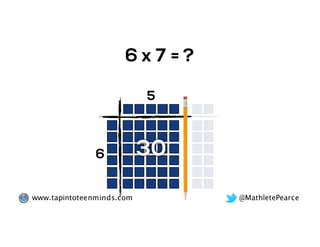
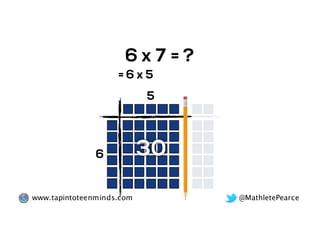
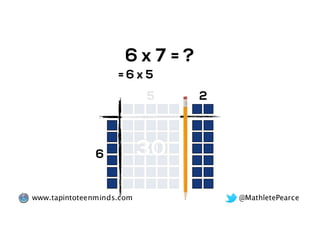
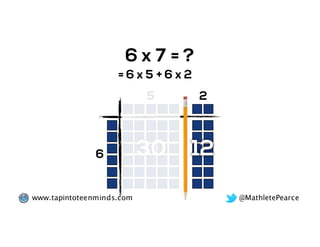
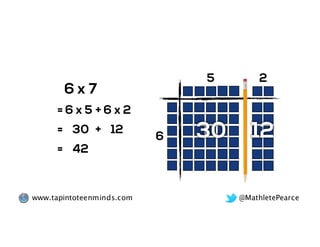
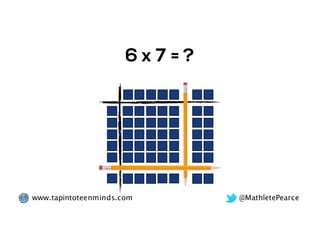
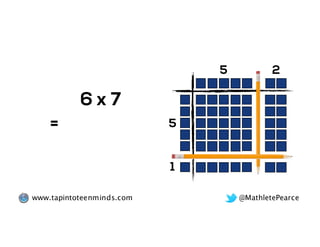
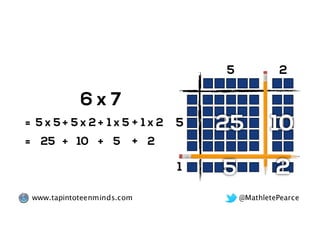
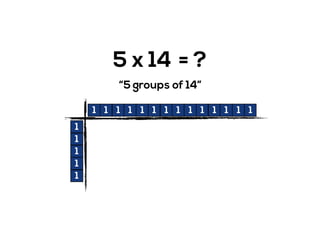
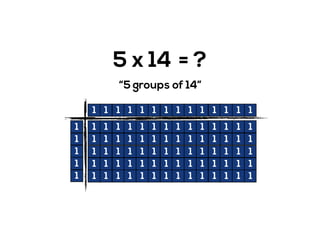
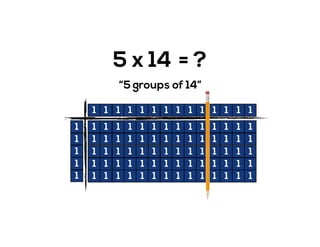
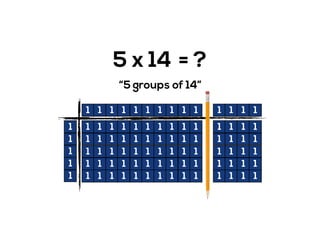
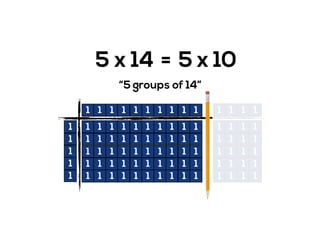
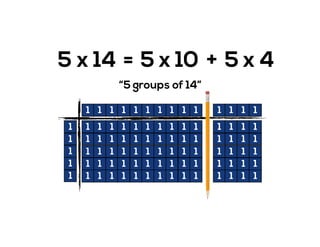
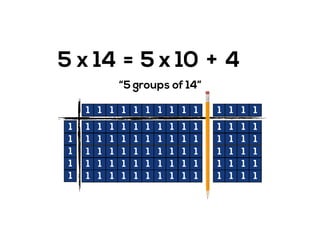
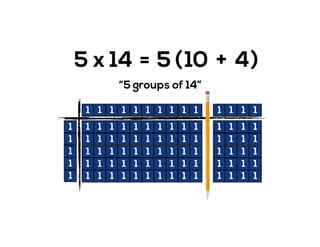
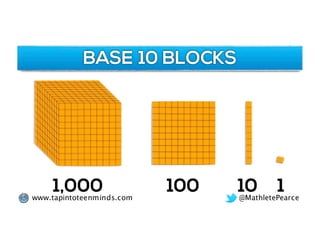
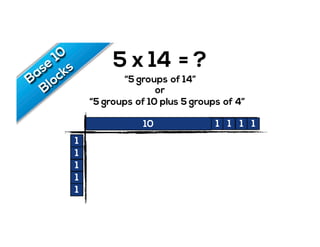
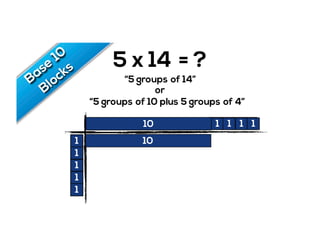
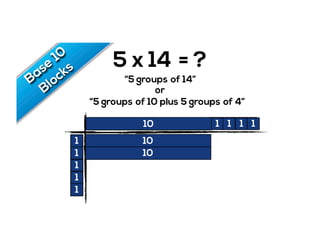
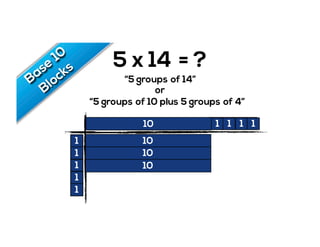
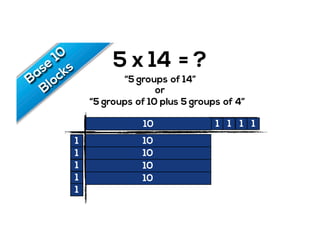
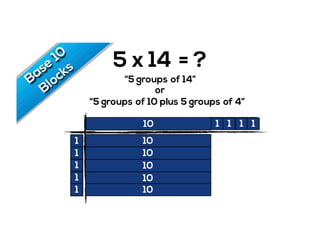
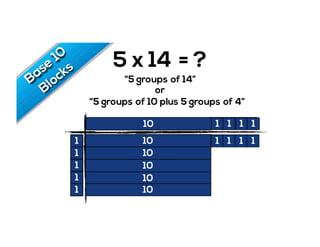
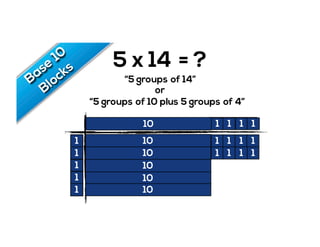
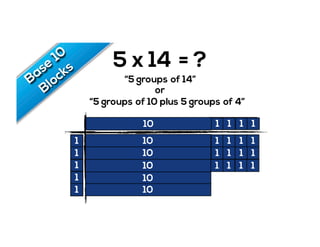
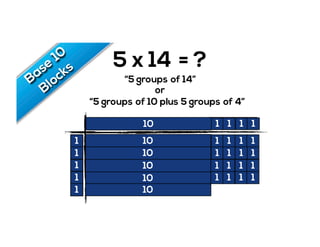
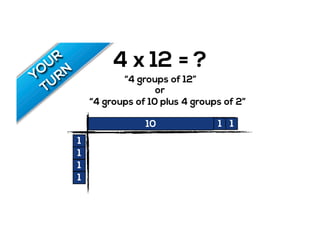
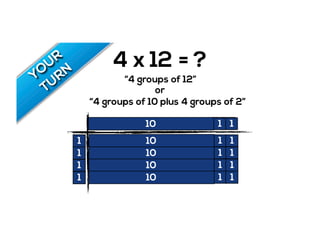
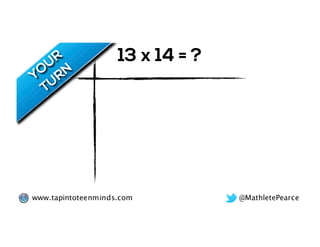
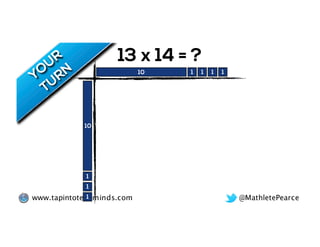
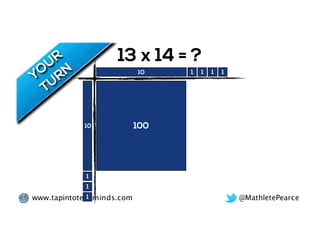
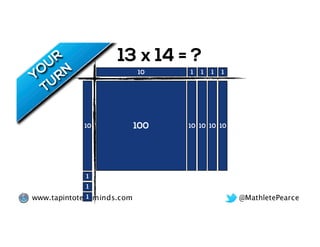
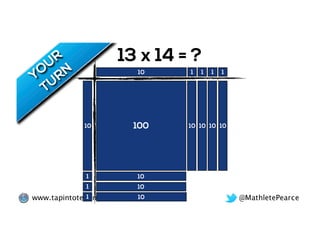
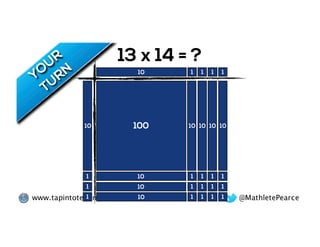
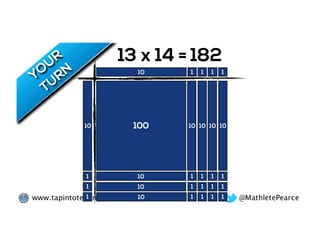
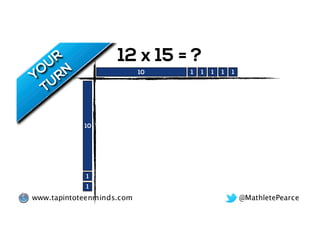
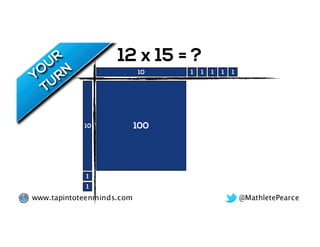
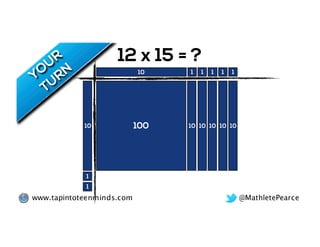
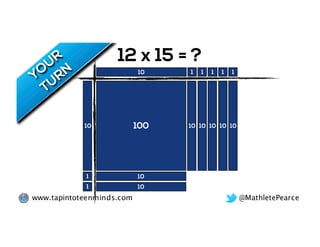
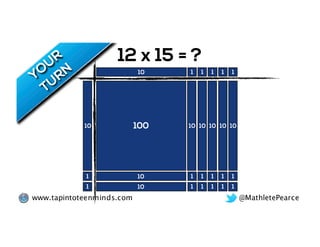
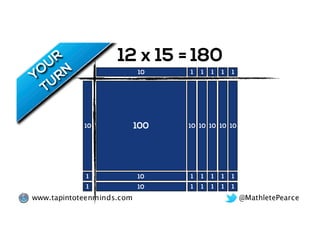
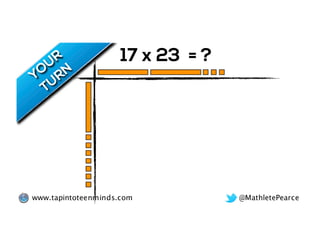
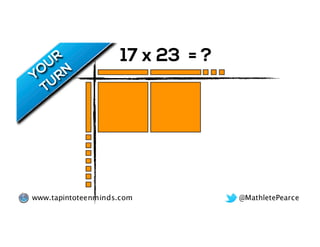
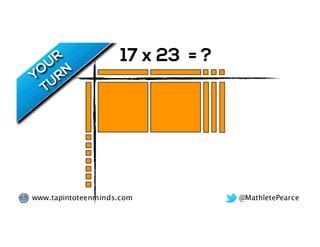
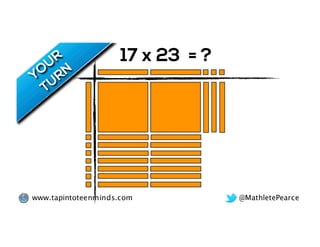
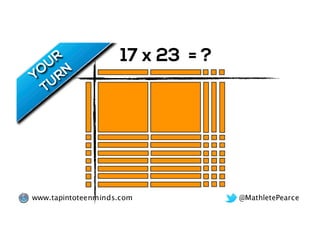
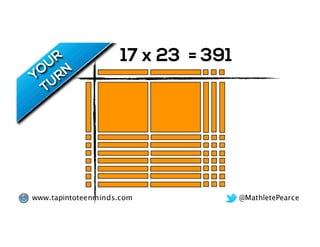
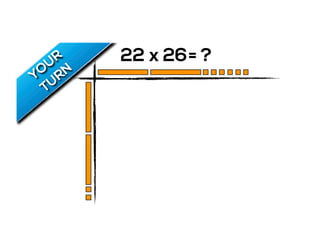
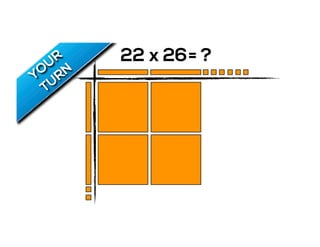
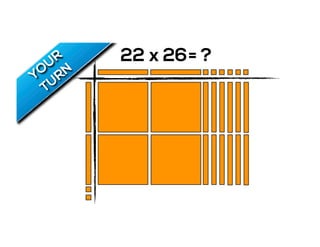
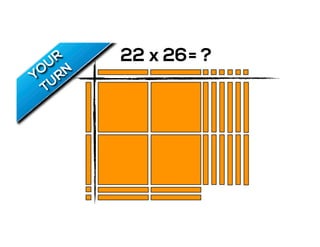
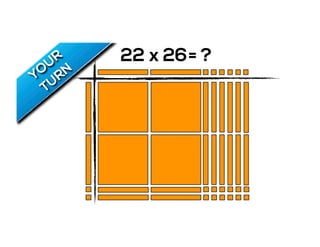
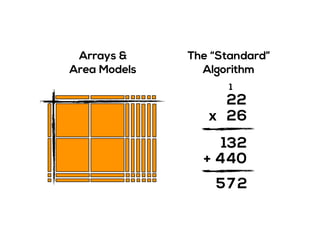
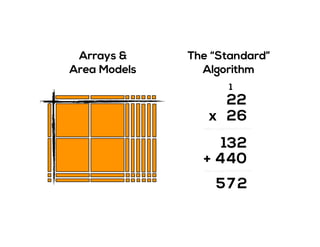
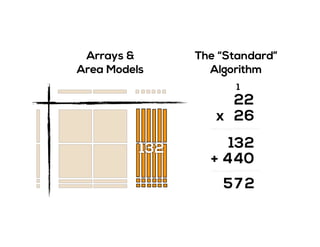
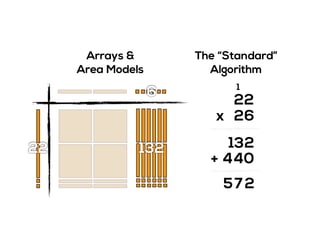
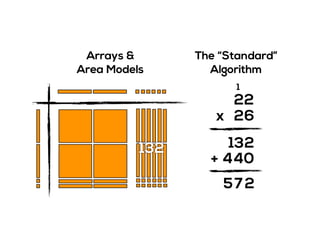
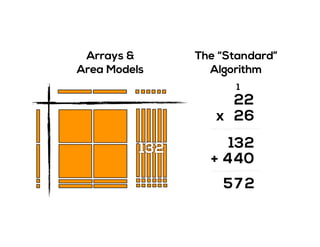
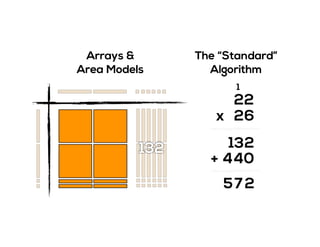
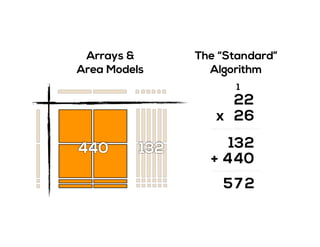
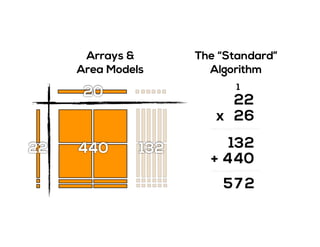
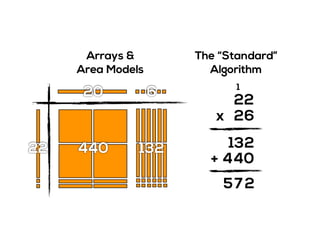
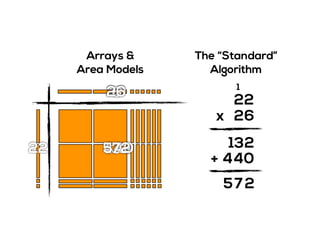
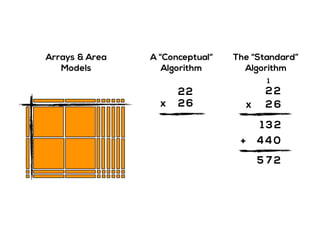
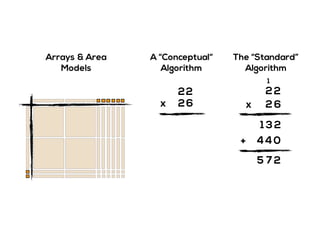
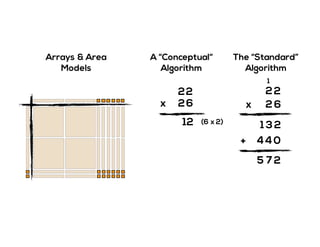
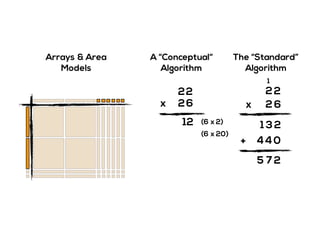
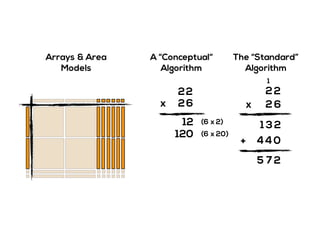
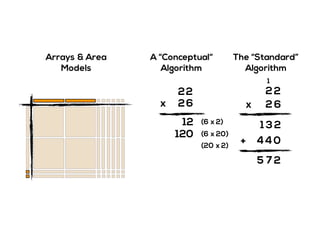
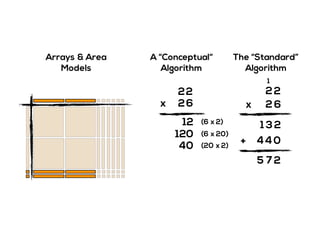
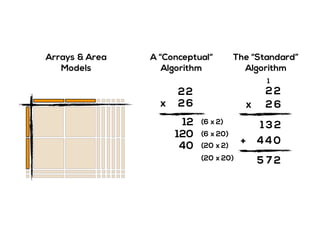
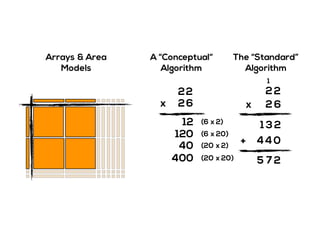
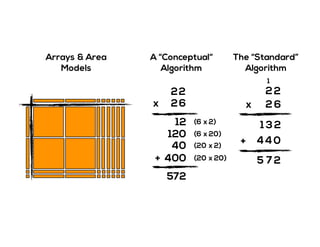
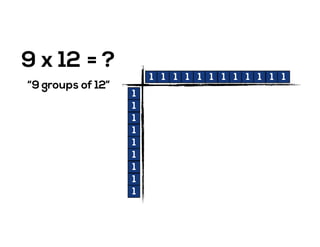
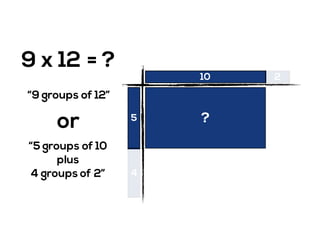
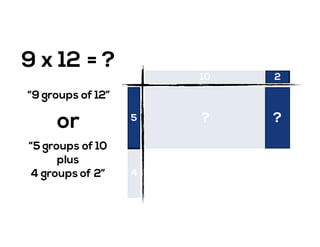
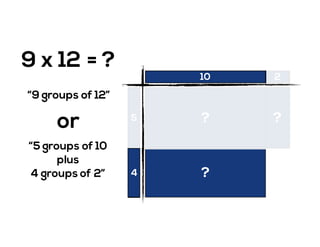
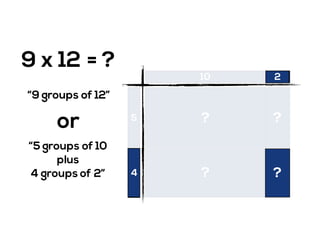
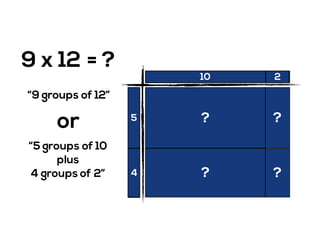
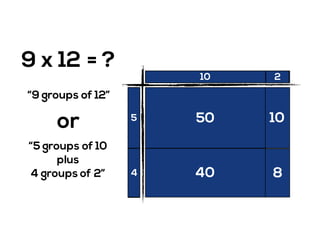
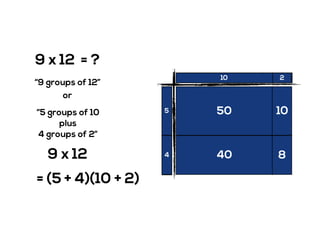
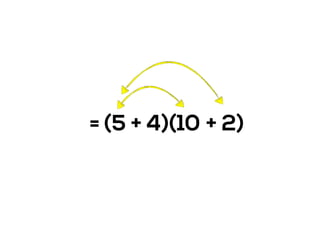
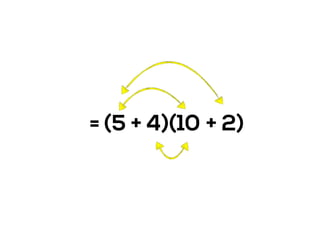
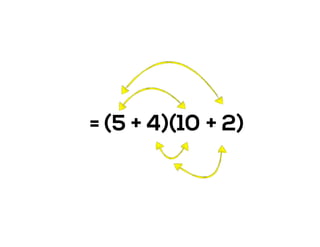
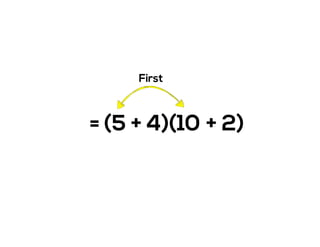
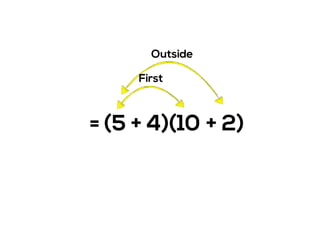
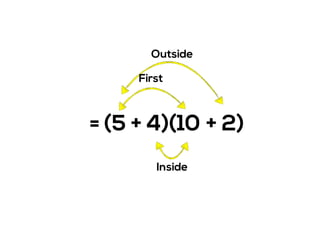
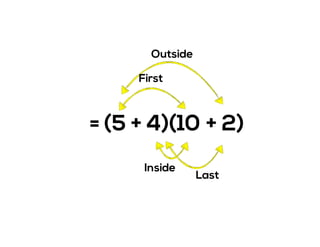
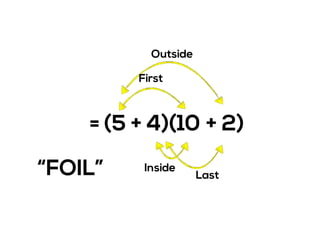
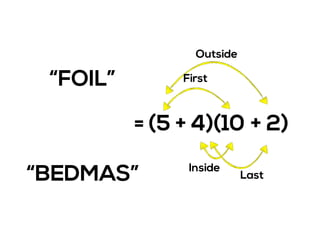
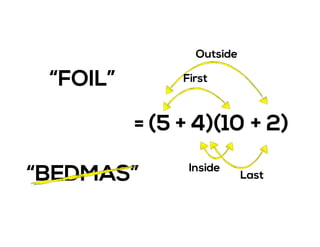
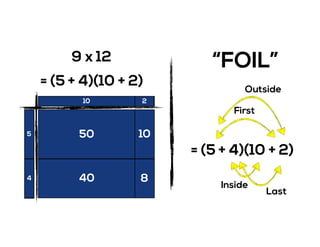
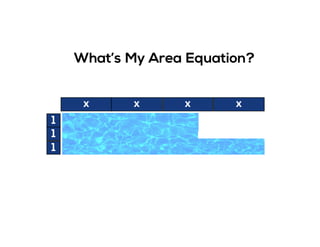
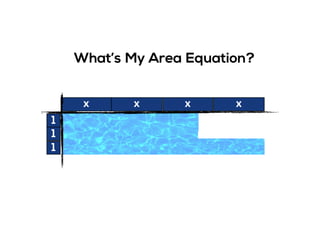
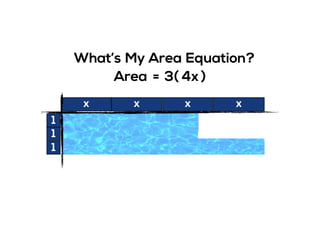
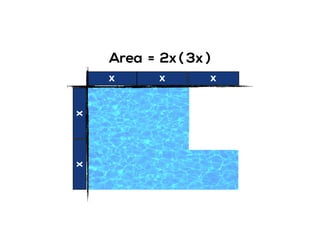
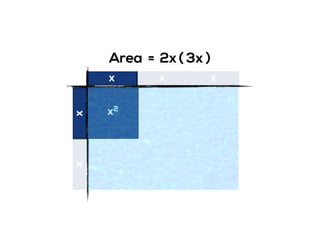
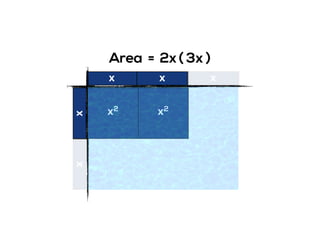
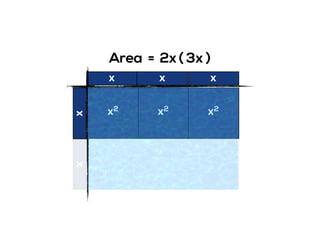
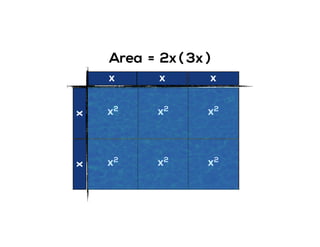
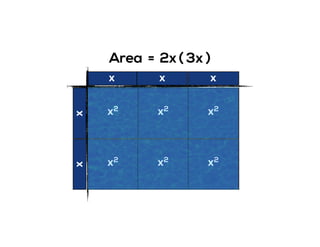
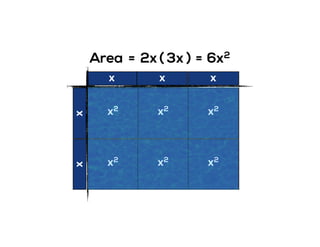
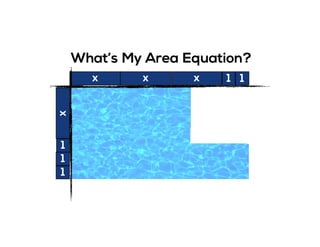
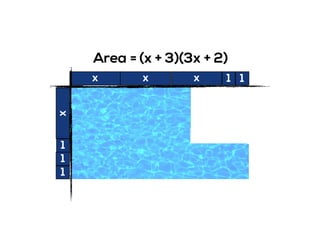
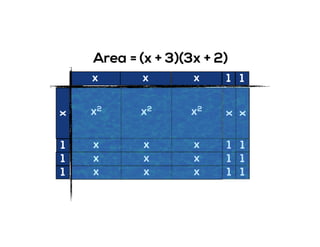
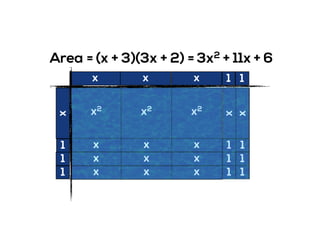
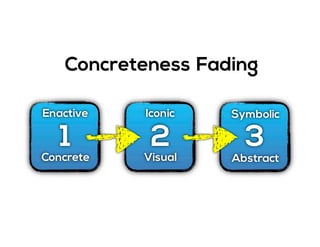
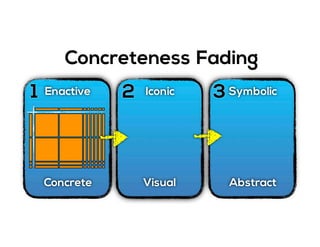
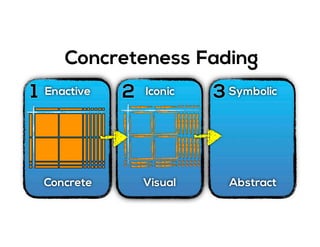
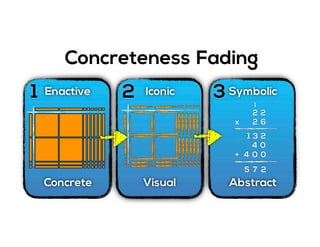
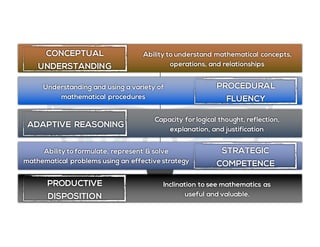
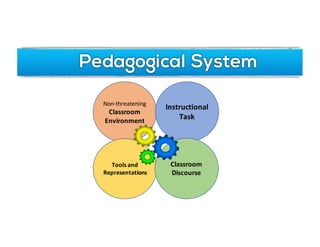
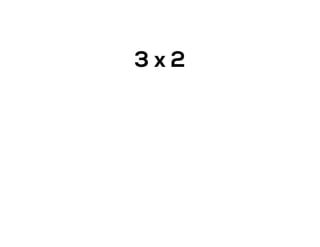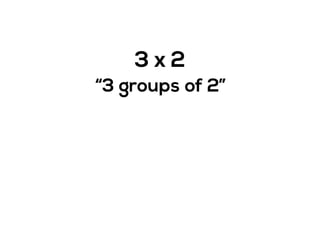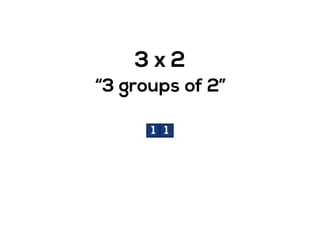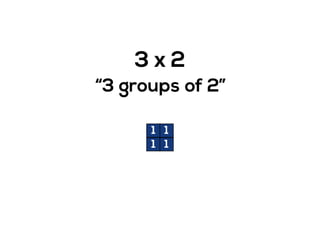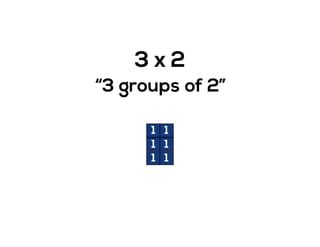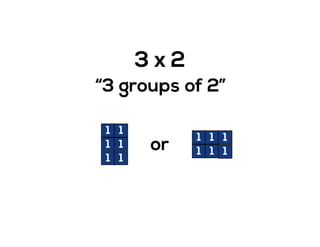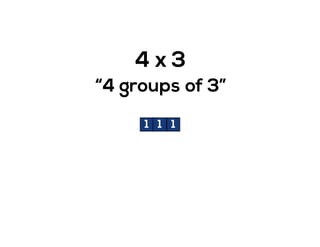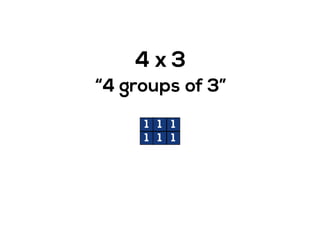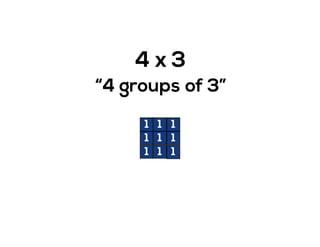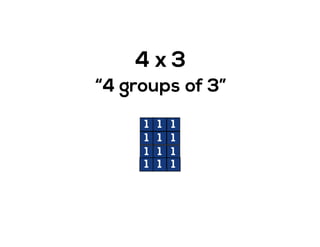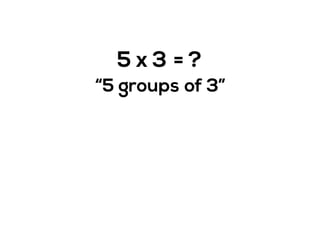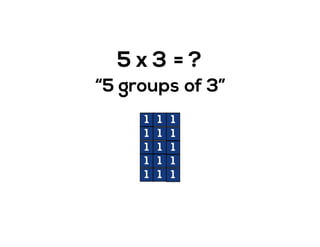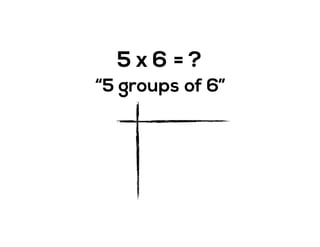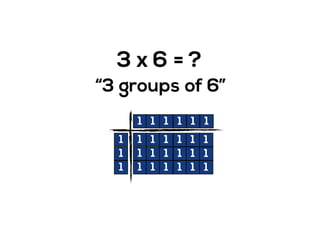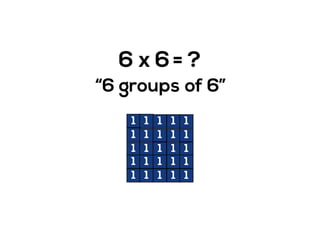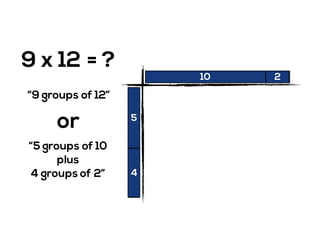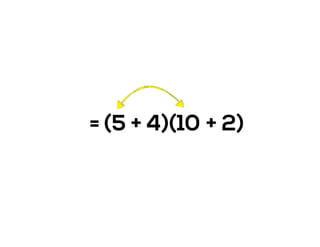The document outlines the agenda for school math learning teams, emphasizing the importance of mathematical vision and proficiency development from K-10. It highlights the necessity for educators to engage students through collaboration, inquiry, and problem-solving while fostering a positive attitude towards mathematics. Additionally, it discusses foundational skills in early mathematics, the role of the math learning team, and the characteristics of effective math education.

1. School Math
Learning Teams

2. AGENDA
MATH VISION
What does it mean to be good at math?
Burning questions
EARLY MATH LEARNING
Counting and Quantity
JUNIOR and INTERMEDIATE MATH
Arrays and Areas Models
PEDAGOGICAL SYSTEMS
Planning a Task
LEADING MATH IN YOUR SCHOOL
The role of the school math learning team

3. TODAY’S LEARNING
We are:
• Extending our understanding of the GECDSB:
Mathematics Vision and Mathematical Proficiencies
• Building an understanding of number sense concepts
from K-10
• Developing an understanding of Pedagogical Systems
• Planning a math task
• Learning to lead math in our schools
Math
Pedagogy
Math
Content
Leadership
&
Professional
Capital

4. THE MATHEMATICS JOURNEY
• Mathematics journey is unlike many others
• It is not an implementation of a program or process
• It is the enaction of the GECDSB Vision

5. The Work: Ambitious and Necessary
Enact the Vision
“The GECDSB provides mathematics education that engages and
empowers students through collaboration, communication, inquiry,
critical thinking and problem-solving, to support each student’s
learning and nurture a positive attitude towards mathematics.”
Table Talk…
Why is this work both ambitious and necessary?

6. SCHOOL MATH TEAM
Click to
add text
Session 1 October
Session 2 November
Session 3 January
Session 4 & 5 February and March
Session 6 April
Table Talk...
What is the role (possible role) of the school math team at your school?
Where are some professional learning spaces in your school?

7. What does it mean to be good
at mathematics?

8. What does it mean to be good at math?
Enjoy learning math
Develop persistence and tenacity
Learn to use math to solve problems
Develop logic and reasoning skills
See the value for mathematics in their world
Learn their facts and mathematical procedures
Understand the ‘whys’ of math

9. GECDSB: A Vision for Mathematics
Strategic Competence
Procedural Fluency
Conceptual Understanding
Adaptive Reasoning
Productive Disposition
This is a vision for mathematics that
is both ambitious and necessary.

10. Math Task Force Data
What does it mean to be good at math?
Math as a functional skill
Math as applied to a profession
Math as a way of thinking and seeing the world

11. Math Vision:
Understanding Proficiency
Strategic Competence
Procedural Fluency
Conceptual Understanding
Adaptive Reasoning
Productive Disposition
Jigsaw: Read Chapter 4

12. Math Task
Click to
add text
How Close to 100?
Instructions can be found at
https://www.youcubed.org/
task/how-to-close-100/

13. Math Task: Consolidation
How do you see this math task
connected to the development of
mathematical proficiency?
Is there are a particular
mathematical proficiency that could
be strengthened through this task?
Does this change your definition of
what it means to be good at math?

14. Does this change your definition of what it
means to be good at math?

15. The Work: Guided By Our Questions
We have many questions about mathematics education.
Table Talk…
With the learners at your table, brainstorm some of the
questions you have or yourstaff may have about mathematics
education.
Share them with the larger group.

16. COFFEE BREAK

17. Early Mathematics
In 2007, it was found that mathematics skills among children in Kindergarten were the
best predictor of later school achievement, regardless of gender or socio-economic
status (Duncan et al., 2007). Kindergarten Program, 2016
Critical Question
How can educators take advantage of the mathematical knowledge and experience that
children have?
Critical Understanding
The presence alone of mathematics in play is insufficient for rich learning to occur
Intentional, purposeful teacher interactions are necessary to ensure that mathematical
learning is maximized during play.

18. Early Mathematics
As educators we must constantly ask ourselves:
Why this learning,
for this student,
at this time?

19. Early Mathematics
What mathematical skills do you think our young learners need?
Number Sense
• Counting
• Quantity Relationships
Geometry and Measurement
are foundational skills that must be in place to support all future
math learning.

20. Counting and Quantity
Conservation
One-to-one
Correspondence
Cardinality
Stable Order
Order
Irrelevance
Abstraction
Movement is
Magnitude
Subitizing
Unitizing

21. Case Study
• What principles of quantity and counting
does the child understand?
• What might be the next step(s) for learning
for this child?

25. Early Mathematics Connections

26. Mathematics
Learning
Teams
M
L
T

27. Counting
and
Quantity
Stable-Order Order Irrelevance
Conservation
One-to-One
Correspondence
Abstraction
Movement is
MagnitudeSubitizing
Unitizing
Cardinality

28. Stable-Order
The list of words used to count must be in a repeatable
order.
This “stable list” must be at least as long as the number of
itemsto be counted.
1
2
3
4
5
6
7 8 9 10

29. Order Irrelevance
The order in which itemsare counted is irrelevant.
1 2 3 4 5 6
1 2 3 4 5 6

30. Conservation
Understanding thatthe count for a set group of objects
stays the same no matterwhether they are spread out or
close together.
7 8 9 10
1 2
3 4
5 6

31. Conservation
Understanding thatthe count for a set group of objects
stays the same no matterwhether they are spread out or
close together.
7 8 9 10
1
2
3 4
5
6

32. … the quantityof five large things is the samecount as a
quantityof five small things or a mixed group of fivesmall
and large things.
Abstraction
…we can count any collection of objects, whether tangible
or not.
1 2
3 4
5
1 2 3 4 5

33. Understanding thateach object being counted must be
given one count and only one count. It is useful in the early
stages for children to actually tag each item being counted
and to movean it out of the way as it is counted.
One-to-One Correspondence
1
2
3
4
5

34. Understanding thatthe last count of a group of objects
represents how many are in the group. A child who
recounts when asked how many candies are in the set that
they just counted, has not understood the cardinality
principle.
Cardinality
1 2 3 4 5 6

35. The ability to 'see' a small amount of objects and know how
many there are without counting.
Subitizing
“5”

36. Understanding thatas you move up the counting sequence
(or forwards), the quantityincreases by one and as you
move down (or backwards), the quantitydecreases by one
or whatever quantityyou are going up/down by.
Movement is Magnitude
1 2 3

37. Understanding thatas you move up the counting sequence
(or forwards), the quantityincreases by one and as you
move down (or backwards), the quantitydecreases by one
or whatever quantityyou are going up/down by.
Movement is Magnitude
1 2 3 4

38. Understanding thatas you move up the counting sequence
(or forwards), the quantityincreases by one and as you
move down (or backwards), the quantitydecreases by one
or whatever quantityyou are going up/down by.
Movement is Magnitude
1 2 3 4 5

39. Understanding thatas you move up the counting sequence
(or forwards), the quantityincreases by one and as you
move down (or backwards), the quantitydecreases by one
or whatever quantityyou are going up/down by.
Movement is Magnitude
1 2 3 4

40. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones

41. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones

42. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones

43. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones

44. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones
1 0

45. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones
1 9

46. Understanding thatin our base ten system objects are
grouped into tens once the count exceeds 9 (and intotens
of tens when it exceeds 99) and that thisis indicated by a 1
in the tens place of a number.
Unitizing
tens ones
2 0

47. PROCEDURAL FLUENCY
STRATEGIC COMPETENCE
ADAPTIVE REASONING
PRODUCTIVE DISPOSITION
CONCEPTUAL
UNDERSTANDING
kylep.ca/gecdsbvision
Math Proficiencies

48. PRODUCTIVE
DISPOSITION
Ability to formulate, represent & solve
mathematical problems using an effective strategy
STRATEGIC
COMPETENCE
PROCEDURAL
FLUENCY
Understanding and using a variety of
mathematical procedures
ADAPTIVE REASONING
Capacity for logical thought, reflection,
explanation, and justification
Inclination to see mathematics as
useful and valuable.
Ability to understand mathematical concepts,
operations, and relationships
CONCEPTUAL
UNDERSTANDING

49. @MathletePearcewww.tapintoteenminds.com
LAST TIME

50. @MathletePearcewww.tapintoteenminds.com

51. @MathletePearcewww.tapintoteenminds.com
Array
Multiplication

52. Array

53. Array

54. Array

55. Array

56. Array

59. 3 x 2

60. 3 x 2
“3 groups of 2”

61. 3 x 2
“3 groups of 2”
1 1

62. 3 x 2
“3 groups of 2”
1 1
1 1

63. 3 x 2
“3 groups of 2”
1 1
1 1
1 1

64. 3 x 2
“3 groups of 2”
1 1
1 1
1 1
1 1
1 1
1
1or

65. 4 x 3

66. 4 x 3
“4 groups of 3”

67. 4 x 3
“4 groups of 3”
1 1 1

68. 4 x 3
“4 groups of 3”
1 1
1 1
1
1

69. 4 x 3
“4 groups of 3”
1 1
1 1
1 1
1
1
1

70. 4 x 3
“4 groups of 3”
1 1
1 1
1 1
1
1
1
1 1 1

71. 4 x 3
“4 groups of 3”
1 1
1 1
1 1
1 1
1 1
1
1or
1
1
1
1 1 1
1
1
1 1 1 1

72. 5 x 3 = ?
“5 groups of 3”

73. 5 x 3
“5 groups of 3”
1 1
1 1
1 1
= ?
1
1
1
1 1
1 1
1
1

74. Virtual Manipulatives
catalog.mathlearningcenter.org/apps

75. Virtual Manipulatives

76. Virtual Manipulatives

77. Virtual Manipulatives

81. 5 x 6
“5 groups of 6”
= ?

82. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1

83. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1
1 1 1 1 1 1

84. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1
1 1 1 1 1 1
1 1 1 11 1 6

85. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1
1 1 1 1 1 1
1 1 1 11 1
1 1 1 11 1
6
12

86. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1
1 1 1 1 1 1
1 1 1 11 1
1 1 1 11 1
1 1 1 11 1
6
12
18

87. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1
1 1 1 1 1 1
1 1 1 11 1
1 1 1 11 1
1 1 1 11 1
1 1 1 11 1
6
12
18
24

88. 5 x 6
“5 groups of 6”
= ?
1
1
1
1
1
1 1 1 1 1 1
1 1 1 11 1
1 1 1 11 1
1 1 1 11 1
1 1 1 11 1
1 1 1 11 1
6
12
18
24
30

89. 1
1
1
3 x 6
“3 groups of 6”
1 1 1 1
= ?
1 1
1 1 1 11 1
1 1 1 11 1
1 1 1 1 1 1

90. 1 1
1
1
1
5 x 5
“5 groups of 5”
1 1 1 1
= ?
1
1
1
1
1 1 1 11
1 1 1 11
1 1 1 11
1 1 1 11
1 1

91. 5 x 5
“5 groups of 5”
1 1 1 1
= 25
1
1 1 1 11
1 1 1 11
1 1 1 11
1 1 1 11

92. 5 x 5
“5 groups of 5”
1 1 1 1
= 25
1
1 1 1 11
1 1 1 11
1 1 1 11
1 1 1 11

93. 5 x 5
“5 groups of 5”
1 1 1 1
= 25
1
1 1 1 11
1 1 1 11
1 1 1 11
1 1 1 11
PERFECT
SQUARE

94. 6 x 6
“6 groups of 6”
1 1 1 1
= ?
1
1 1 1 11
1 1 1 11
1 1 1 11
1 1 1 11

95. 6 x 6
“6 groups of 6”
1 1 1 1
= 36
1
1 1 1 11
1 1 1 11
1 1 1 11
1 1 1 11
1
1
1
1
1
1 1 1 11 1

99. What’s the Length of the Pool?
?

100. 1
1
1
1
What’s the Length of the Pool?
?

101. 1
1
1
1
What’s the Length of the Pool?
1 1 1 1

102. 1
1
1
1
What’s the Length of the Pool?
1 1 1 1 1 1 1 1

103. 1
1
1
1
What’s the Length of the Pool?
1 1 1 1 1 1 1 1 1 1 1 1

104. 1
1
1
1
What’s the Length of the Pool?
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

105. 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?

106. 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?

107. 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?

108. 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?

109. 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?

110. 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?
1 1 1
1 1 1
1 1 1
1
1
1
1 1 1 1

111. 1 1 1
1 1 1
1 1 1
1
1
1
1 1 1 1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?
16 16 16 16

112. 1 1 1
1 1 1
1 1 1
1
1
1
1 1 1 1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?
16 16 16 1664

113. 1 1 1
1 1 1
1 1 1
1
1
1
1 1 1 1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?
16 16 16 1664 square-units

114. 1 1 1
1 1 1
1 1 1
1
1
1
1 1 1 1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
What’s the Area of the Pool?
16 16
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
64 square-units

116. “Spatial thinking, or reasoning,
involves the location and
movement of objects and
ourselves, either mentally or
physically, in space. It is not a
single ability or process but actually
refers to a considerable number of
concepts, tools and processes.”
(National Research Council, 2006)

117. “The relation between spatial
ability and mathematics is so
well established that it no longer
makes sense to ask whether
they are related…”
“…moreover, spatial thinking
was a better predictor of
mathematics success than either
verbal or mathematical skills.”

118. Activities to Develop Geometric
and Spatial Thinking
visualizing diagramming
designing
(Davis, Okamoto & Whiteley, 2015)
orienting
locating
perspective taking
sliding
rotating
reflecting
modeling
exploring symmetry
composing
decomposing
scaling
map-making

122. 1
1
1
3 x 6
“3 groups of 6”
1
= ?
1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1

123. = 18
1
1
1
3 x 6
“3 groups of 6”
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1

124. = 18
1
1
1
3 x 6
“3 groups of 6”
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1

125. = 18
1
1
1
3 x 6
“Splitting the Array”
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1

126. = 18
1
1
1
3 x 6
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1
3 x 4=

127. = 18
1
1
1
3 x 6
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1
3 x 4=

128. = 18
1
1
1
3 x 6
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1
3 x 4= + 3 x 2

129. = 18
1
1
1
3 x 6
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1
3 x 4= + 3 x 2
12= + 6

130. = 18
1
1
1
3 x 6
1 1
1 1
1
1 1 11
1 1 11
1 1 11 1
1 1 1 1 1 1
3 x 4= + 3 x 2
12= + 6
3(= +4 2)

131. @MathletePearcewww.tapintoteenminds.com
=6 x 7 ?

132. @MathletePearcewww.tapintoteenminds.com
6 x 7 = ?

133. @MathletePearcewww.tapintoteenminds.com
6 x 7 = ?

134. @MathletePearcewww.tapintoteenminds.com
6 x 7 = ?

135. @MathletePearcewww.tapintoteenminds.com
6 x 7 = ?

136. @MathletePearcewww.tapintoteenminds.com
6 x 7 = ?

137. @MathletePearcewww.tapintoteenminds.com
= 426 x 7

138. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7

139. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7

140. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7

141. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7
5
6

142. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7
5
6 30

143. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7
5
6 30
= 6 x 5

144. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7
5
6 30
= 6 x 5
2

145. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7
5
6 30
= 6 x 5
2
12
+ 6 x 2

146. @MathletePearcewww.tapintoteenminds.com
6 x 7
5
6 30
= 6 x 5
2
12
+ 6 x 2
= 30 + 12
= 42

147. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7

148. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7

149. @MathletePearcewww.tapintoteenminds.com
= ?6 x 7

150. @MathletePearcewww.tapintoteenminds.com
=
5
5
2
1
6 x 7

151. @MathletePearcewww.tapintoteenminds.com
=
5
5
2
1
5 x 5 5 x 2 1 x 5 1 x 2+ + +
6 x 7

152. @MathletePearcewww.tapintoteenminds.com
6 x 7
=
5
5 25
2
10
1
5 x 5 5 x 2 1 x 5 1 x 2+ + +
= 25 10 5 2+ + +
5 2

153. 5 x 14 = ?
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1

154. 5 x 14 = ?
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1

155. 5 x 14 = ?
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1

156. 5 x 14 = ?
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1

157. 5 x 14 =
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
x 105

158. 5 x 14 =
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
+x 105 x 45

159. 5 x 14 =
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
+x 105 x 45

160. 5 x 14 =
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1
+(105 )45

161. @MathletePearcewww.tapintoteenminds.com
BASE 10 BLOCKS
1001,000 10 1

162. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1

163. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10

164. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10

165. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10

166. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10
10

167. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10
10
10

168. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10
10
10
1 1 1 1

169. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10
10
10
1 1 1 1
1 1 1 1

170. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10
10
10
1 1 1 1
1 1 1 1
1 1 1 1

171. 5 x 14 = ?
“5 groups of 14”
“5 groups of 10 plus 5 groups of 4”
or
1 1 1 1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
1
1
1
1
1
10
10
10
10
10
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1

172. 1 1 1 1
5 x 14 = ?
“5 groups of 14”
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1 1 110
5
“5 groups of 10 plus 5 groups of 4”
or
1
1
1
1
1
10
10
10
10
10
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1

173. 4 x 12 = ?
“4 groups of 12”
“4 groups of 10 plus 4 groups of 2”
or
1 1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110
1
1
1
1

174. 4 x 12 = ?
“4 groups of 12”
“4 groups of 10 plus 4 groups of 2”
or
1 1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110
1
1
1
1
1 110
1 110
1 110
1 110

175. @MathletePearcewww.tapintoteenminds.com
13 x 14 = ?

176. @MathletePearcewww.tapintoteenminds.com
13 x 14 = ?
1 110 1 1
10
1
1
1

177. @MathletePearcewww.tapintoteenminds.com
13 x 14 = ?
1 110 1 1
10
1
1
1
100

178. @MathletePearcewww.tapintoteenminds.com
13 x 14 = ?
1 110 1 1
10
1
1
1
100 10 10 10 10

179. @MathletePearcewww.tapintoteenminds.com
13 x 14 = ?
1 110 1 1
10
1
1
1
100 10 10 10 10
10
10
10

180. @MathletePearcewww.tapintoteenminds.com
13 x 14 = ?
1 110 1 1
10
1
1
1
100 10 10 10 10
10
10
10
1 1 1 1
1 1 1 1
1 1 1 1

181. @MathletePearcewww.tapintoteenminds.com
13 x 14 = 182
1 110 1 1
10
1
1
1
100 10 10 10 10
10
10
10
1 1 1 1
1 1 1 1
1 1 1 1

182. @MathletePearcewww.tapintoteenminds.com
12 x 15 = ?
1 110 1 1 1
10
1
1

183. @MathletePearcewww.tapintoteenminds.com
1 110 1 1 1
10
1
1
100
12 x 15 = ?

184. @MathletePearcewww.tapintoteenminds.com
1 110 1 1 1
10
1
1
100 10 10 10 10 10
12 x 15 = ?

185. @MathletePearcewww.tapintoteenminds.com
1 110 1 1 1
10
1
1
100 10 10 10 10 10
10
10
12 x 15 = ?

186. @MathletePearcewww.tapintoteenminds.com
1 110 1 1 1
10
1
1
100 10 10 10 10 10
10
10
1 1 1 1 1
1 1 1 1 1
12 x 15 = ?

187. @MathletePearcewww.tapintoteenminds.com
1 110 1 1 1
10
1
1
100 10 10 10 10 10
10
10
1 1 1 1 1
1 1 1 1 1
12 x 15 = 180

188. @MathletePearcewww.tapintoteenminds.com
17 x 23 = ?

189. @MathletePearcewww.tapintoteenminds.com
17 x 23 = ?

190. @MathletePearcewww.tapintoteenminds.com
17 x 23 = ?

191. @MathletePearcewww.tapintoteenminds.com
17 x 23 = ?

192. @MathletePearcewww.tapintoteenminds.com
17 x 23 = ?

193. @MathletePearcewww.tapintoteenminds.com
17 x 23 = 391

194. 22 x 26= ?

195. 22 x 26= ?

196. 22 x 26= ?

197. 22 x 26= ?

198. 22 x 26= ?

199. 2
2x
2
6
The “Standard” Algorithm

200. 2
2x
2
6
The “Standard” Algorithm

201. 2
2x
2
6
2
1
The “Standard” Algorithm

202. 2
2x
2
6
2
1
The “Standard” Algorithm

203. 2
2x
2
6
2
1
The “Standard” Algorithm

204. 2
2x
2
6
2
1
12
The “Standard” Algorithm

205. 2
2x
2
6
1
213
The “Standard” Algorithm

206. 2
2x
2
6
1
213
The “Standard” Algorithm

207. 2
2x
2
6
1
213
The “Standard” Algorithm

208. 2
2x
2
6
1
0
213
The “Standard” Algorithm

209. 2
2x
2
6
1
04
213
The “Standard” Algorithm

210. 2
2x
2
6
1
04
213
The “Standard” Algorithm

211. 2
2x
2
6
2
1
1
04
3
The “Standard” Algorithm

212. 2
2x
2
6
2
1
1
04
3
The “Standard” Algorithm

213. 2
2x
2
6
1
044
213
The “Standard” Algorithm

214. 2
2x
2
6
1
044
213
The “Standard” Algorithm
+

215. 2
2x
2
6
1
044
213
The “Standard” Algorithm
+
275

216. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275

217. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275

218. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
132

219. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
13222
6

220. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
132

221. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
132

222. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
132

223. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
132440

224. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
13244022
20

225. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
13244022
20 6

226. The “Standard”
Algorithm
Arrays &
Area Models
2
2x
2
6
1
044
213
+
275
13244022
206
572
26

227. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

228. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

229. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

230. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
(6 x 20)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

231. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
120 (6 x 20)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

232. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
120 (6 x 20)
(20 x 2)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

233. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
120 (6 x 20)
40 (20 x 2)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

234. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
120 (6 x 20)
40 (20 x 2)
(20 x 20)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

235. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
120 (6 x 20)
40 (20 x 2)
400 (20 x 20)
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

236. Arrays & Area
Models
A “Conceptual“
Algorithm
2
2x
2
6
12 (6 x 2)
120 (6 x 20)
40 (20 x 2)
400 (20 x 20)
572
+
The “Standard”
Algorithm
2
2x
2
6
1
044
21 3
+
275

237. 9 x 12 = ?
“9 groups of 12”
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 1

238. 9 x 12 = ?
“9 groups of 12” 1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
“5 groups of 10
plus
4 groups of 2”
or

239. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
?
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or

240. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
? ?
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or

241. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
?
?
?
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or

242. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
?
?
?
?
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or

243. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
?
?
?
?
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or

244. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
50
40
10
8
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or

245. 9 x 12 = ?
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
50
40
10
8
“9 groups of 12”
“5 groups of 10
plus
4 groups of 2”
or
9 x 12
= (5 + 4)(10 + 2)

246. = (5 + 4)(10 + 2)

247. = (5 + 4)(10 + 2)

248. = (5 + 4)(10 + 2)

249. = (5 + 4)(10 + 2)

250. = (5 + 4)(10 + 2)
First

251. = (5 + 4)(10 + 2)
First
Outside

252. = (5 + 4)(10 + 2)
First
Outside
Inside

253. = (5 + 4)(10 + 2)
First
Outside
Inside
Last

254. = (5 + 4)(10 + 2)
First
Outside
Inside
Last“FOIL”

255. = (5 + 4)(10 + 2)
First
Outside
Inside
Last
“FOIL”
“BEDMAS”

256. = (5 + 4)(10 + 2)
First
Outside
Inside
Last
“FOIL”
“BEDMAS”

257. 9 x 12
1
1
1
1
1
1
1
1
1
1 1 1 1 1 1 1 1 1 1 1 110 2
5
4
50
40
10
8
= (5 + 4)(10 + 2)
= (5 + 4)(10 + 2)
First
Outside
Inside
Last
“FOIL”

260. What’s My Area Equation?

261. What’s My Area Equation?
x x x x

262. What’s My Area Equation?
x x x x
1
1
1

263. What’s My Area Equation?
x x x x
1
1
1

264. What’s My Area Equation?
x x x x
1
1
1
Area = 3( )4x

265. What’s My Area Equation?
x x x x
1
1
1
x x x x
x x x x
x x x x
Area = 3( )4x
= 12x units2

266. x x x xx
Area = 2x ( )3x

267. x x x xx
x2
Area = 2x ( )3x

268. x2
x x x xx
x2
Area = 2x ( )3x

269. x2x2
x x x xx
x2
Area = 2x ( )3x

270. x x x xx
x2 x2 x2
x2 x2 x2
Area = 2x ( )3x

271. x x x xx
x2 x2 x2
x2 x2 x2
Area = 2x ( )3x

272. x x x xx
x2 x2 x2
x2 x2 x2
Area = 2x ( )3x

273. x x x xx
x2 x2 x2
x2 x2 x2
6x2Area = 2x ( )3x =

276. What’s My Area Equation?x
1 1
1
1
x
1
x x

277. Area = (x + 3)(3x + 2)x
1 1
1
1
x
1
x x

278. x
1 1
1
1
x
1
x x
x2 x2 x2
x x x
x x x
x x x
x
x
1
1
1
1
1
1
Area = (x + 3)(3x + 2)

279. x
1 1
1
1
x
1
x x
x2 x2 x2
x x x
x x x
x x x
x
x
1
1
1
1
1
1
Area = (x + 3)(3x + 2) = 3x2 + 11x + 6

280. Concreteness Fading
1 2 3
Enactive
Concrete
Iconic
Visual
Symbolic
Abstract

281. Concreteness Fading
1 2 3Enactive
Concrete
Iconic
Visual
Symbolic
Abstract

282. Concreteness Fading
1 2 3Enactive
Concrete
Iconic
Visual
Symbolic
Abstract

283. Concreteness Fading
1 2 3Enactive
Concrete
Iconic
Visual
Symbolic
Abstract
2
2x
2
6
1
04
004
21 3
+
275

284. PROCEDURAL FLUENCY
STRATEGIC COMPETENCE
ADAPTIVE REASONING
PRODUCTIVE DISPOSITION
CONCEPTUAL
UNDERSTANDING
kylep.ca/gecdsbvision
Math Proficiencies

285. PRODUCTIVE
DISPOSITION
Ability to formulate, represent & solve
mathematical problems using an effective strategy
STRATEGIC
COMPETENCE
PROCEDURAL
FLUENCY
Understanding and using a variety of
mathematical procedures
ADAPTIVE REASONING
Capacity for logical thought, reflection,
explanation, and justification
Inclination to see mathematics as
useful and valuable.
Ability to understand mathematical concepts,
operations, and relationships
CONCEPTUAL
UNDERSTANDING

286. Leading Mathematics Learning:
Building Confidence
What’s your next best move?

287. In Math Class
Table Talk…
What would we see, hear and feel in an exemplary
math class?
Write one idea per sticky note.
Identify the groups with a heading/theme/category.

288. Pedagogical System
Non-threatening
Classroom
Environment
Instructional
Task
Tools and
Representations
Classroom
Discourse

289. In Math Class
Table Talk…
Fold the chart paper into quarters to reflect the
4 aspects of the pedagogical system.
Do your ideas fit/match these categories?
What other ideas can you add?
Instructional
Task
Non-
threatening
Classroom
Environment
Tools and
Representations
Classroom
Discourse

290. Pedagogical System: Understanding
Task
What is a Math Task?
Anyproblem or set of problemsthat focuses students'attention on a
particular mathematical ideaand/or providesan opportunitytodevelopor
use a particular mathematical habit of mind.
High or Low CognitiveDemand
The cognitive demandof a task is the levelof cognitive engagement needed
to completethe task (Stein et al. 2009).

291. A task by itself is not rich;
it is what we do with the task and
how it connects to the pedagogical
system that makes it rich.
Understanding Task

292. Bump It Up
Bump up a task as an Assessmentfor Learning
• Use the Task Cards at your table
• Grade, Topic, Overall Expectation and a Task
• Use the Mathematics Curriculum and find
the specific expectations
• Re-write the task

293. Task: Assessment for Learning
Tom Schimmer’s (Grading From the Inside Out, 2016) premise is that
all assessment practices should be put through two filters:
1. Is it accurate?
2. Does it promote confidence/optimism in students?
“School is no longer about the completion of a series of activities,
but rather the pursuit of proficiency as a set of outcomes that
students achieve through the instructional experience”

294. Understanding Math Tasks
Grade 2
Topic: Counting
Overall Expectations: read, represent, compare, and order whole
numbers to 100, and use concrete materials to represent fractions and
money amounts to 100¢
Specific Expectation(s): count forward by 1’s, 2’s, 5’s, 10’s, and 25’s to
200, using number lines and hundreds charts, starting from multiples of
1, 2, 5, and 10 (e.g., count by 5’s from 15; count by 25’s from 125)
Task
Count by 2s
Task: Assessment for Learning

295. What was your task?
What did you notice about the curriculum?
What/How can the task be modified, refined, extended to support ALL
students?
CCoonnssiiddeerr
- students with persistent learning challenges
- students identified as gifted
How could you use this learning to lead math learning in your school?
Understanding Task:
Consolidation

296. Understanding Math Tasks
If you deny students the opportunity to
engage in this activity – to pose their own
problems, to make their own conjectures and
discoveries, to be wrong, to be creatively
frustrated, to have an inspiration, to cobble
together their own explanations and proofs –
you deny them mathematics itself.
Paul Lockhart, A Mathematician’s Lament, 2009
Mathematics Learning

297. Understanding Math Tasks
Quotations about mathematics by mathematicians.
• Choose 1 that connects with your thinking
• Explain your choice and your thinking
Building Confidence in our Next Best Move…
What is your next best move?
Leading Math Learning
in Our Schools

298. Bring student work based on a mathematics task.
Consider
Curriculum expectation
Assessment for Learning
We will analyze the task in the context of pedagogical system.
For Next Time…

299. What was one (or more) key learning(s) from today?
What was one thing you would have changed in the day?
What questions do you still have?
What learning would you like to see for next session?
Feedback