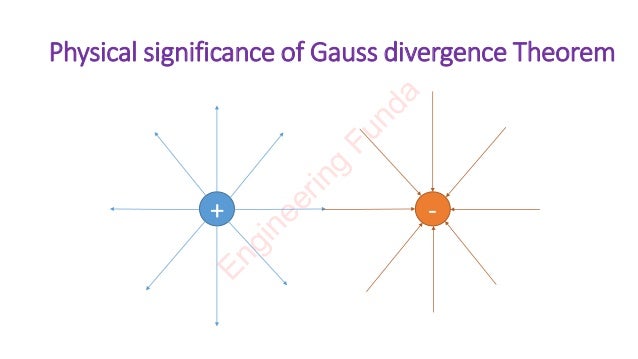
The Gauss divergence theorem explains the relationship between volume and surface integration. It states that the flux of a vector field out of a closed surface is equal to the total divergence of that field over the volume enclosed by the surface. The theorem can be used to understand electromagnetics, fluid mechanics, fields like gravity and electromagnetism, and aerodynamics. It also helps explain the location of sources and sinks of a vector field and the rate of change of a function with respect to position.

1. By Prof. Hitesh Dholakiya
Gauss Divergence
Theorem
Electromagnetics
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a
Engineering Funda Android App Electromagnetic Theory YT Playlist

2. Basics of Gauss Divergence Theorem
Statement of Gauss Divergence Theorem
Proof of Gauss Divergence Theorem
Physical significance of Gauss Divergence Theorem
Outlines of Session
Use of Gauss Divergence Theorem
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a
Engineering Funda Android App Electromagnetic Theory YT Playlist

3. Basics of Gauss Divergence Theorem
❖ Divergence theorem explains relationship in between volume integration and surface
integration.
❖ Divergence theorem also use to see the location of source and sink.
❖ Divergence theorem explains rate of change of function with respect to position.
❖ Divergence is flux density, it explains how much flux is entering or leaving the source
or sink.
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a
Engineering Funda Android App Electromagnetic Theory YT Playlist

4. Function of Gauss Divergence Theorem
❖ Mathematically Divergence theorem expressed as
ර 𝑃. 𝑑𝑆 = ර ∇ . 𝑃 𝑑𝑉
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a

5. Proof of Gauss Divergence Theorem
❖ Divergence of any function 𝑷 can be calculated by
❖ So further calculation can be done by
❖ So for total volume
𝐷𝑖𝑣 𝑃 = ∇. 𝑃 = lim
∆𝑉→0
‫ׯ‬ 𝑃 𝑑𝑆
∆𝑉
⇒ lim
∆𝑉→0
∇. 𝑃 ∆𝑉 = lim
∆𝑉→0
ර 𝑃 𝑑𝑆
ර 𝑃. 𝑑𝑆 = ර ∇ . 𝑃 𝑑𝑉
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a

6. Physical significance of Gauss divergence Theorem
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a

7. Physical significance of Gauss divergence Theorem
+ -
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a

8. Use of Gauss Divergence Theorem
❖ It is used in applications of fluid mechanics
❖ It is used to understand electromagnetics
❖ It is used to understand flaw of fields (e.g. Gravitational fields, Electric field, Magnetic
field etc)
❖ It is used in aerodynamics.
E
n
g
i
n
e
e
r
i
n
g
F
u
n
d
a