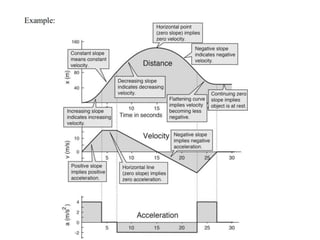
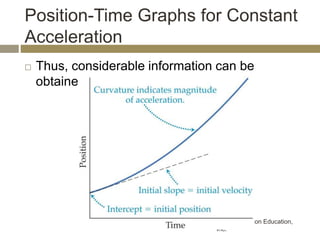
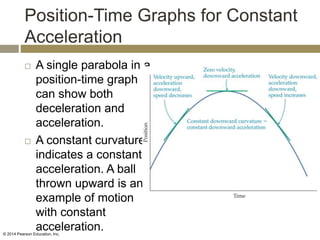
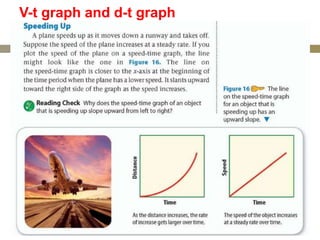
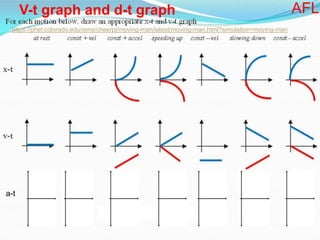
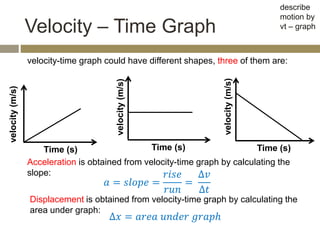
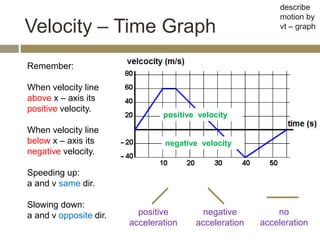
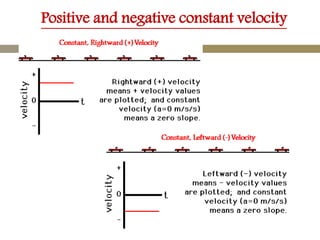
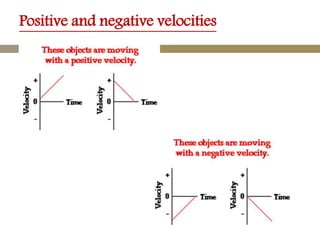
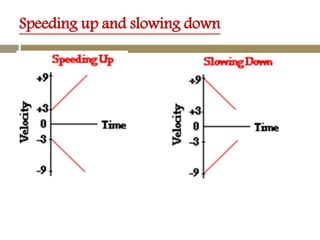
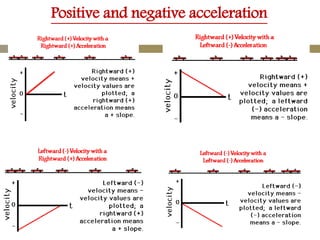
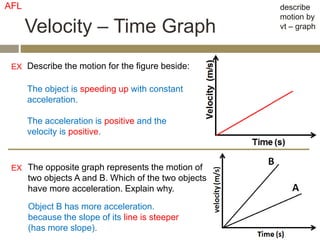
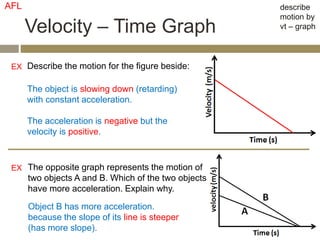
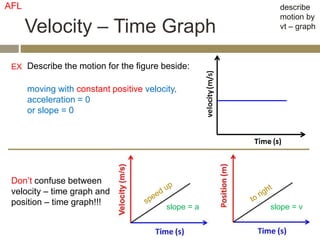
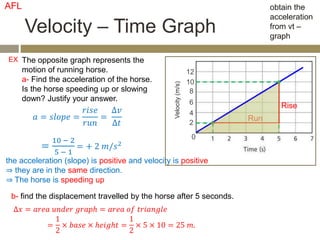
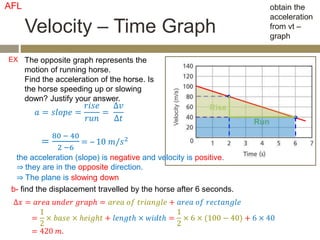
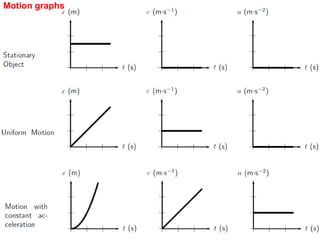
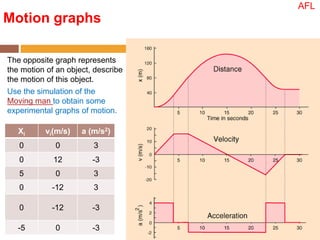
The velocity vector for an object in uniform circular motion is tangential to the circle. The velocity vector is always tangent to the circular path. It is changing direction but constant in magnitude. It is never directed toward or away from the center. The radius of the circle does not affect the velocity. The answer is A.

1. TOPIC 2.3 – POSITION-
TIME GRAPHS FOR
CONSTANT
ACCELERATION
GRADE 9 PHYSICS

2. Lesson Objectives:

4. Position-Time Graphs for Constant
Acceleration
 The Position-time
graph for a uniformly
accelerated object is
a parabola.
 The greater the
curvature of the
parabola, the
greater the
magnitude of the
acceleration
© 2014 Pearson Education, Inc.

5. Position-Time Graphs for Constant
Acceleration
 Constant acceleration produces a parabolic
position-time graph.
 The sign of the acceleration determines
whether the parabola has an upward or
downward curvature.
© 2014 Pearson Education,
Inc.

6. Position-Time Graphs for Constant
Acceleration
 The magnitude of the acceleration is related to
how sharply a position-time graph curves. In
general, the greater the curvature of the
parabola, the greater the magnitude of the
acceleration.
© 2014 Pearson Education,
Inc.

7. Position-Time Graphs for Constant
Acceleration
 Each term in the equation
has graphical meaning.
 The vertical intercept is equal to the initial position
xi.
 The initial slope is equal to the initial velocity.
 The sharpness of the curvature indicates the
magnitude of the acceleration.

8. Position-Time Graphs for Constant
Acceleration
 Thus, considerable information can be
obtained from a position-time graph.
© 2014 Pearson Education,
Inc.

9. Position-Time Graphs for Constant
Acceleration
 A single parabola in a
position-time graph
can show both
deceleration and
acceleration.
 A constant curvature
indicates a constant
acceleration. A ball
thrown upward is an
example of motion
with constant
acceleration.
© 2014 Pearson Education, Inc.

10. V-t graph and d-t graph

11. V-t graph and d-t graph

12. V-t graph and d-t graph

13. V-t graph and d-t graph

14. V-t graph and d-t graph
a-t
AFL
https://phet.colorado.edu/sims/cheerpj/moving-man/latest/moving-man.html?simulation=moving-man

15. Velocity – Time Graph
describe
motion by
vt – graph
velocity-time graph could have different shapes, three of them are:
Time (s)
velocity
(m/s)
Time (s)
velocity
(m/s)
Time (s)
velocity
(m/s)
Acceleration is obtained from velocity-time graph by calculating the
slope:
𝑎 = 𝑠𝑙𝑜𝑝𝑒 =
𝑟𝑖𝑠𝑒
𝑟𝑢𝑛
=
Δ𝑣
Δ𝑡
Displacement is obtained from velocity-time graph by calculating the
area under graph:
∆𝑥 = 𝑎𝑟𝑒𝑎 𝑢𝑛𝑑𝑒𝑟 𝑔𝑟𝑎𝑝ℎ

16. Velocity – Time Graph
Remember:
When velocity line
above x – axis its
positive velocity.
When velocity line
below x – axis its
negative velocity.
Speeding up:
a and v same dir.
Slowing down:
a and v opposite dir.
positive velocity
negative velocity
positive
acceleration
negative
acceleration
no
acceleration
describe
motion by
vt – graph

17. Positive and negative constant velocity

18. Positive and negative velocities

19. Speeding up and slowing down

20. Positive and negative acceleration

21. Velocity – Time Graph
describe
motion by
vt – graph
Describe the motion for the figure beside:
EX
The object is speeding up with constant
acceleration.
The acceleration is positive and the
velocity is positive.
The opposite graph represents the motion of
two objects A and B. Which of the two objects
have more acceleration. Explain why.
EX
Object B has more acceleration.
because the slope of its line is steeper
(has more slope).
AFL

22. Velocity – Time Graph
describe
motion by
vt – graph
Describe the motion for the figure beside:
EX
The object is slowing down (retarding)
with constant acceleration.
The acceleration is negative but the
velocity is positive.
The opposite graph represents the motion of
two objects A and B. Which of the two objects
have more acceleration. Explain why.
EX
Object B has more acceleration.
because the slope of its line is steeper
(has more slope).
AFL

23. Velocity – Time Graph
describe
motion by
vt – graph
Describe the motion for the figure beside:
EX
moving with constant positive velocity,
acceleration = 0
or slope = 0
Don’t confuse between
velocity – time graph and
position – time graph!!!
slope = a slope = v
AFL

24. Velocity – Time Graph
obtain the
acceleration
from vt –
graph
The opposite graph represents the
motion of running horse.
a- Find the acceleration of the horse.
Is the horse speeding up or slowing
down? Justify your answer.
EX
2
0
4
6
8
10
12
Velocity
(m/s)
Rise
Run
𝑎 = 𝑠𝑙𝑜𝑝𝑒 =
𝑟𝑖𝑠𝑒
𝑟𝑢𝑛
=
Δ𝑣
Δ𝑡
=
10 − 2
5 − 1
= + 2 𝑚/𝑠2
the acceleration (slope) is positive and velocity is positive
⇒ they are in the same direction.
⇒ The horse is speeding up
∆𝑥 = 𝑎𝑟𝑒𝑎 𝑢𝑛𝑑𝑒𝑟 𝑔𝑟𝑎𝑝ℎ = 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒
b- find the displacement travelled by the horse after 5 seconds.
=
1
2
× 𝑏𝑎𝑠𝑒 × ℎ𝑒𝑖𝑔ℎ𝑡 =
1
2
× 5 × 10 = 25 𝑚.
AFL

25. Velocity – Time Graph
obtain the
acceleration
from vt –
graph
The opposite graph represents the
motion of running horse.
Find the acceleration of the horse. Is
the horse speeding up or slowing
down? Justify your answer.
EX
𝑎 = 𝑠𝑙𝑜𝑝𝑒 =
𝑟𝑖𝑠𝑒
𝑟𝑢𝑛
=
Δ𝑣
Δ𝑡
=
80 − 40
2 −6
= ‒ 10 𝑚/𝑠2
Velocity
(m/s)
Run
Rise
the acceleration (slope) is negative and velocity is positive.
⇒ they are in the opposite direction.
⇒ The plane is slowing down
∆𝑥 = 𝑎𝑟𝑒𝑎 𝑢𝑛𝑑𝑒𝑟 𝑔𝑟𝑎𝑝ℎ = 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡𝑟𝑖𝑎𝑛𝑔𝑙𝑒 + 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑟𝑒𝑐𝑡𝑎𝑛𝑔𝑙𝑒
b- find the displacement travelled by the horse after 6 seconds.
=
1
2
× 𝑏𝑎𝑠𝑒 × ℎ𝑒𝑖𝑔ℎ𝑡 + 𝑙𝑒𝑛𝑔𝑡ℎ × 𝑤𝑖𝑑𝑡ℎ =
1
2
× 6 × (100 − 40) + 6 × 40
= 420 𝑚.
AFL

26. Motion graphs

27. Motion graphs
The opposite graph represents
the motion of an object, describe
the motion of this object.
Use the simulation of the
Moving man to obtain some
experimental graphs of motion.
Xi vi(m/s) a (m/s2)
0 0 3
0 12 -3
5 0 3
0 -12 3
0 -12 -3
-5 0 -3
AFL

28. Guided example

29. CW
Centripetal acceleration always points to the
of the circle.
A. back
B. center
C. front
D. outer edge

30. CW

31. CW

32. Assessment

33. Assessment
9. The velocity vector for an object in
uniform
circular motion is .
A. tangential to the circle
B. directed toward the center of the circle
C. directed away from the center of the
circle
D. proportional to the radius of the circle