The document provides an overview of functional programming, including its key features, history, differences from imperative programming, and examples using Lisp and Scheme. Some of the main points covered include: - Functional programming is based on evaluating mathematical functions rather than modifying state through assignments. - It uses recursion instead of loops and treats functions as first-class objects. 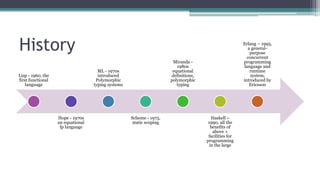- Lisp was the first functional language in 1960 and introduced many core concepts like lists and first-class functions. Scheme was developed in 1975 as a simpler dialect of Lisp. - Functional programs are more focused on what to compute rather than how to compute it, making them more modular and easier to reason about mathematically.

1. Functional
Programming
Girish Khanzode

2. Contents
• Key Features
• LISP
• Scheme
• Predicate Functions
• Lambda Calculus
• Tail Recursive Function
• Higher-Order Functions
• Static Lexical Scoping
• Delayed Evaluation
• Anonymous Functions
• Currying
• Bound and Free variables
• References

3. Definition
• A style of programming with basic method of computation as
application of functions to arguments
• Mimics mathematical functions to the greatest extent possible
• Abstract nature leads to considerably simpler programs
• Supports new ways to structure and reason about programs
• More focused on what to compute than how

4. Definition
• Functions as first-class objects
• Supports high-order functions
• Recursion instead of loop constructs - tail recursion
• Lists as basic data structures
• Avoids side effects - no shared state
• Suitable for parallel execution

5. History
Lisp - 1960, the
first functional
language
Hope - 1970s
an equational
fp language
ML - 1970s
introduced
Polymorphic
typing systems
Scheme - 1975,
static scoping
Miranda -
1980s
equational
definitions,
polymorphic
typing
Haskell –
1990, all the
benefits of
above +
facilities for
programming
in the large
Erlang – 1995,
a general-
purpose
concurrent
programming
language and
runtime
system,
introduced by
Ericsson

6. Imperative vs. Functional
• Imperative languages – design based on von Neumann architecture
▫ Efficiency is primary concern than suitability of the language for
software development
▫ Operations are done and the results are stored in variables for later use
▫ Management of variables is a constant concern and source of complexity
• Functional languages - design based on mathematical functions
▫ Theoretical basis
▫ Unconcerned with the architecture of the machines on which programs
will run

7. Imperative vs. Functional
• Concept of a variable
▫ In imperative programming languages, variables refer to memory
locations that store values
▫ In math, variables always stand for actual values
• Assignment statements
▫ In imperative languages, assignments allow memory locations to be reset
with new values
▫ In math, there are no concepts of memory location and assignment

8. Necessary Features
• 1st class and high-order functions
• Serious polymorphism
• Powerful list facilities
• Recursion
• Structured function returns
• Fully general aggregates
• Garbage collection

9. Key Features
• A mathematical approach to the concept of a variable
▫ Treats computation as evaluation of mathematical functions
▫ Variables are bound to values, not memory locations
▫ Variable value cannot change - eliminates assignment as an available
operation
• Most FPL retain some notion of assignment
▫ Possible to create a pure functional program that takes a strictly
mathematical approach to variables

10. Key Features
• Lack of assignment makes loops impossible
▫ A loop requires a control variable whose value changes as the loop
executes
▫ Recursion is used instead of loops
• No internal state of a function
▫ Value depends only on the values of its arguments and possibly nonlocal
variables

11. Key Features
• Function value cannot depend on the order of evaluation of its
arguments
▫ An advantage for concurrent applications
• Data and programs represented in the same way
• Lack of local state - opposite of OO programming wherein
computation proceeds by changing the local state of objects

12. Key Features
• Functions must be general language objects, viewed as values
themselves
• Functions are first-class data values
▫ Can be passed as arguments
▫ Can be returned as a value
▫ Can be put into a data structure as a value
▫ Can be the value of an expression

13. Key Features
• All procedures are functions that distinguish incoming parameters
from outgoing results
• Programs have no explicit state
• Programs constructed entirely by composing expressions
• Value of a function depends only on its parameters, not on order of
evaluation or execution path

14. Referential Transparency
• A function has the property of referential transparency if its value
depends only on the values of its parameters.
• the evaluation of a function always produces the same result given
the same parameters
• Similar to a constant
• Referential transparency means that equals can be replaced by
equals

15. Example Code
Imperative style Functional style
• x := 0; i := 1; j := 100;
• while i < j do
x := x + i*j; i := i + 1;
j := j – 1
• end while
• return x
f(x,i,j) == if i < j then
f (x+i*j, i+1, j-1)
else x

16. Why Functional Programming
• Designed to support problem solving
• Many features to design clear, concise, abstract, modular, correct
and reusable solutions to problems
• Allows formulation of solutions to problems to be as easy, clear, and
intuitive as possible
• Lack of side effects makes programs easier to understand

17. Why Functional Programming
• Modularity - built by combining well understood simpler functions
• Programs are easy to write - system relieves the user from dealing
with many tedious implementation considerations such as memory
management, variable declaration…
• Concise programs - typically 1/10th of non-FPL program
• Programs easy to understand - programs have mathematical
properties

18. Why Functional Programming
• Functional programs are referentially transparent - if a variable is set to be
a certain value in a program, that value cannot be changed again
• Programs are easy to reason about - they are just mathematical functions
• Can prove or disprove claims about programs using familiar mathematical
methods and ordinary proof techniques (encountered in high school
algebra)
• Can always replace left hand side of a function definition by corresponding
right hand side

19. Mathematical Functions
• A mapping of members of one set, called the domain set, to another
set, called the range set
• Functional Composition
▫ A function takes two functions as parameters and produces another
function as its returned value
▫ In math, the composition operator o is defined as
 if f:XY and g:YZ, then g o f:XZ is given by (g o f)(x) = g(f(x))
 Hence, if f(x) x+2 and g(x)3*x then h  f°g gives (3*x)+2

20. Mathematical Functions
• Construction - A functional form that takes a list of functions as
parameters and yields a list of the results of applying each of its
parameter functions to a given parameter
Form: [f, g]
For f (x)  x * x * x and g (x)  x + 3,
[f, g] (4) yields (64, 7)

21. LISP
• A first language with many features of modern FPLs
• Defined by John McCarthy ~1958 as a language for AI
• Lists stored internally as single-linked lists
• LISP meaning - LIST Processing
• Based on the Lambda calculus
• Lambda notation is used to specify functions and function
definitions
• Function applications and data have same form

22. LISP
• If list (A B C) is interpreted as data it is a simple list of three atoms
A, B, and C
• If interpreted as function application, it means function A applied to
two parameters B and C
• Uniform representation of programs and data using a single general
structure: list
• Interpreter written in the same language
• Automatic memory management by runtime system
• Many variations

23. Scheme
• A new LISP-like Language
• Defined in mid 70 by Sussman and Steele (MIT)
• Goals
▫ move Lisp back toward it’s simpler roots
▫ incorporate ideas which had been developed in the PL community since
1960
• Designed to be a cleaner, modern and simpler version than the
contemporary dialects of LISP
• Uses static scoping and a more uniform treatment of functions
• All programs and data considered expressions

24. Scheme
• Designed with very few regular constructs to support a variety of
programming styles
▫ Functional, object-oriented, and imperative
• All data types are equal
▫ What one can do to one data type, one can do to all data types
• Functions are first-class
▫ Can be values of expressions and elements of lists
▫ Can be assigned to variables and passed as parameters

25. Elements of Scheme
• Syntax expressed in extended Backus-Naur form
notation
▫ -> means - is defined as
▫ | indicates alternative
▫ {} encloses an item seen zero or more times
▫ ‘ ‘ encloses a literal item
• Syntax of Scheme - expression  atom | ‘(‘ {expression}
’)’ atom  number | string | symbol | character |
Boolean

26. Elements of Scheme
• Standard evaluation rules
▫ Parameters are evaluated in no particular order
▫ Values of the parameters substituted into the function body
▫ Function body is evaluated
▫ Value of the last expression in the body is value of the function

27. Elements of Scheme
• Types of expressions
▫ Atoms: Anything that can’t be decomposed further such as a string of
characters beginning with a letter, number or special character
 2, #t, #f, “hello”, foo, bar
 #t = true, #f = false
▫ Parenthesized expression: a sequence of zero or more expressions
separated by spaces and surrounded by parentheses
• All expressions must be written in prefix form
▫ (+ 2 3)
 + is a function applied to values 2 and 3 to return 5

28. Elements of Scheme

29. Elements of Scheme
• Example: (* (+ 2 3) (+ 4 5 ))
▫ Two additions are evaluated first, then the multiplication

30. Elements of Scheme
• Value of a function (as an object) is clearly distinguished from a call
to the function
▫ Function is represented by the first expression in an application
▫ Function call is surrounded by parentheses
• Applicative order evaluation
▫ All sub-expressions are evaluated first
▫ A corresponding expression tree is evaluated from leaves to root

31. Elements of Scheme
• Primitive arithmetic functions
▫ +, -, *, /, ABS, SQRT, REMAINDER, MIN, MAX
• Loops are provided by recursive call
• Numeric Predictor Functions
▫ #T is true and #F is false (sometimes () is used for false)
▫ =, <>, >, <, >=, <=
▫ EVEN?, ODD?, ZERO?, NEGATIVE?

32. Elements of Scheme - Quote
• Problem arises when data are represented directly in a program, such as a
list of numbers
• Example: (2.1 2.2 3.1)
▫ Scheme will try to evaluate it as a function call
▫ Must prevent this and consider it to be a list literal, using a special form with the
keyword quote
• Example: (quote (2.1 2.2 3.1))
• Rule for evaluating a quote special form is to simply return the expression
following quote without evaluating it

33. Elements of Scheme
• Loops are provided by recursive call
• Selection is provided by special forms:
▫ if form: like an if-else construct
▫ cond form: like an if-elseif construct; cond stands for conditional
expression
• Neither the if nor the cond special form obey the standard
evaluation rule
▫ If they did, all arguments would be evaluated each time, rendering them
useless as control mechanisms

34. Elements of Scheme
• Scheme function applications use pass by value, while special forms
in Scheme and Lisp use delayed evaluation

35. Define
• A function to construct functions
• Creates a global binding of a variable visible in top-level environment
• Forms
▫ bind a symbol to an expression
(DEFINE pi 3.141593)
(DEFINE two_pi (* 2 pi))
▫ bind names to lambda expressions
(DEFINE (square x) (* x x))
(square 5)
• First parameter never evaluated
• Second parameter evaluated and bound to first

36. Predicate Functions
• Run-time tests to determine kind of variable when they are
un-typed
• Eq?
▫ Takes two symbolic parameters
▫ Returns #T if both are atoms and same else #F
▫ (EQ? 'A 'A) yields #T
▫ (EQ? 'A 'B) yields #F
▫ If called with list parameters, result unreliable
▫ Does not work for numeric atoms

37. Predicate Functions
• List?
▫ Returns #T if parameter is a list else #F
• Null?
▫ Returns #T if parameter is empty list else #F
▫ Returns #T if parameter is()
• Number? : is argument a number
• Symbol? : is argument a symbol
• Atom? : if argument is an atom

38. Scheme Functions - Let
• Similar to temporary variable declarations in block-structured
languages
• Provides a local environment and scope for a set of variable names
▫ Similar to temporary variable declarations in block-structured languages
▫ Values of the variables can be accessed only within the let form, not
outside it
• Binds a variable to a value within an expression
▫ (let ((a 2) (b 3)) (+ 1 b))
▫ First expression in a let is a binding list

39. Scheme Functions - Let
• Values of the variables can be accessed only within the let form
• Binding a name to a lambda within a let
▫ (let ((circlearea (lambda (radius) (* 3.14 (* radius radius))))) (circlearea
10))
• Letrec - special form that works like a let
▫ Allows arbitrary recursive references within the binding list
▫ (letrec ((factorial (lambda (n) (if (= n 0) 1 (* n (factorial (- n 1)))))))
(factorial 10)

40. Scheme Functions - equalsimp
• Takes two lists as parameters
• returns #T if two lists equal, #F otherwise
define (EQUALSIMP lis1 lis2)
(cond
((null? lis1) (null? lis2))
((null? lis2) #F)
((eq? (car lis1) (car lis2)) (EQUALSIMP (cdr lis1) (cdr lis2)))
(else #F)
))

41. Scheme Functions - member
• Takes an atom and a list
• Returns #T if atom in list else #F
define (member? x list)
(if (null? list) #f
(if (equal? x (car list)) #t
(member? x (cdr list)))))

42. Scheme Functions - append
• Given two lists as parameters, returns first list with the elements of
the second list appended
(define (append list1 list2)
(if (null? list1) list2
(cons (car list1) (append (cdr list1) list2))))

43. Scheme Functions - equal
• Given two lists as parameters, returns #T if two lists are equal, #F otherwise
(DEFINE (equal lis1 lis2)
(COND
((NOT (LIST? lis1))(EQ? lis1 lis2))
((NOT (LIST? lis2)) #F)
((NULL? lis1) (NULL? lis2))
((NULL? lis2) #F)
((equal (CAR lis1) (CAR lis2))
(equal (CDR lis1) (CDR lis2)))
(ELSE #F)
))

44. Lambda Calculus
• A notation/model of computation based
on purely syntactic symbol manipulation,
in which everything is a function
• Mathematical abstraction
• Special form based on  notation
• Defines function parameters and body
• Nameless function
• Format: (LAMBDA (x) (* x x )
▫ x is called a bound variable
▫ (lambda (radius) (* 3.14 (* radius radius)))
• A reduction rule permits 2 to be substituted for x in the
lambda, yielding this: ( .x + 1 x) 2  1+2  3

45. Lambda Calculus
• Variables do not occupy memory
• Set of constants and variables not specified by the grammar
• In the expression
▫ x is bound by lambda
▫ The expression E is the scope of the binding
▫ Free occurrence: any variable occurrence outside the scope
▫ Bound occurrence: an occurrence that is not free
• Different occurrences of a variable can be bound by different
lambdas
• Some occurrences of a variable may be bound, while others are free

46. Lambda Calculus
• Applicative order evaluation vs. normal order evaluation
▫ pass by value vs. pass by name
▫ Evaluate expression:
▫ Use applicative order – replace (+ 2 3) by its value and then
applying beta-reduction
▫ Use normal order - apply beta-reduction first and then evaluation
• Normal order evaluation is delayed evaluation

47. Lambda Calculus
• Church-Rosser theorem: reduction sequences are essentially
independent of the order in which they are performed
▫ Id λx.x
▫ Const λx.2
▫ Plus λx.λy.x + y
▫ Square λx.x * x
▫ Hypot λx. λy.sqrt (plus (square x) (square y))

48. Dynamic Type Checking
• Scheme’s semantics include dynamic type checking
▫ Only values have data types
▫ Types of values not checked until necessary at runtime
• Automatic type checking happens right before a primitive function - such as
+
• Arguments to programmer-defined functions not automatically checked
• If wrong type Scheme halts with an error message
• Use built-in type recognition functions like number? and procedure? to
check a value’s type

49. List - Basic Data Structures in
Scheme• List can be visualized as a pair
of values: the car and the cdr
▫ List L is a pointer to a box of
two pointers, one to its car and
the other to its cdr
• Box and pointer notation for a
simple list (1 2 3)
• Black rectangle in the end box
stands for the empty list ( )

50. Box and Pointer Notation for List
• List L = ((a b) c (d))

51. Programming Techniques in
Scheme• Scheme relies on recursion to perform loops and other repetitive operations
▫ To apply repeated operations to a list, “cdr down and cons up”: apply the
operation recursively to the tail of a list and then use the cons operator to
construct a new list with the current result
• Example:
(define square-list (lambda (L)
(if (null? L) '()
(cons (* (car L) (car L)) (square-list
(cdr L)))))

52. List Functions
• All basic list manipulation done using functions car, cdr, cons, and null?
• CAR
▫ accesses the head of the list
▫ (CAR '(A B C)) yields A
▫ (CAR '((A B) C D)) yields (A B)
• CDR
▫ returns the tail of the list (minus the head)
▫ (CDR '(A B C)) yields (B C)
▫ (CDR '((A B) C D)) yields (C D)

53. List Functions
• CONS
▫ adds a new head to an existing list
▫ (CONS 'A '(B C)) returns (A B C)
▫ X = 2 and Y = (3 4 5) : (cons x y)  (2 3 4 5)
▫ X = () and Y =(a b c) : (cons x y)  (() a b c)
▫ X = a and Y =() : (cons x y )  (a)
• null? : returns true if list is empty or false otherwise

54. Tail Recursive Function
• A function call is tail recursive if there is nothing to do after the
function returns except return its value
• Recursive call is the last step
• Scheme compiler translates function to code having a loop with no
additional overhead for function calls other than the top-level call
▫ Eliminates performance hit of recursion
• Loops preferred to recursion in imperative languages
▫ Avoids runtime overhead of procedure calls

55. Tail Recursive Function

56. Tail and Non-Tail Recursion

57. Tail and Non-Tail Recursion
• After each recursive call, the value returned by the call must be
multiplied by n (the argument to the previous call)
• Requires a runtime stack to track the value of this argument for each
call as the recursion unwinds
• Entails a linear growth of memory and a substantial performance hit

58. Tail and Non-Tail Recursion
• All the work of computing values is done when the arguments are
evaluated before each recursive call
• Argument result is used to accumulate intermediate products on the
way down through the recursive calls
• No work remains to be done after each recursive call, so no runtime
stack is necessary to remember arguments of previous calls

59. Higher-Order Functions
• Take other functions as parameters
• Can return functions as values
• (define make-double (lambda (f) (lambda (x) (f x x)))
• Apply-to-all functional form
▫ Takes a single function as a parameter
▫ Yields a list of values obtained by applying the given function to each element of a list of
parameters
▫ Form: 
For h(x)x*x
(h,(2,3,4)) yields (4,9,16)

60. Static Lexical Scoping
• Modern dialects Scheme and Common Lisp are statically scoped
• Early dialects of Lisp were dynamically scoped
• Static scope is the area of a program in which a variable declaration
is visible
▫ For static scoping, the meaning or value of a variable can be determined
by reading the source code
▫ For dynamic scoping, the meaning depends on the run-time context
• Declaration of variables can be nested in block-structured languages

61. Static Lexical Scoping
• Scope of a variable extends to the end of the block in which it is
declared, including any nested blocks (unless it is re-declared within
a nesting block)
• Free variable: a variable referenced within a function that is not also
a formal parameter to that function and is not bound within a
nested function
• Bound variable: a variable within a function that is also a formal
parameter to that function

62. Static Lexical Scoping
• Lexical scoping fixes the meaning of free variables in one place in
the code, making a program easier to read and verify than dynamic
scoping

63. Delayed Evaluation
• Evaluate all expressions only if needed
• Example: (if a b c) - Evaluation of b and c must be delayed until the
result of a is known; then either b or c is evaluated, but not both
• Useful for large or infinite streams of data
• Usually implemented using closures – data structures containing
all the information required to evaluate the expression
• Equivalent to call-by-name

64. Delayed Evaluation
• Short-circuit evaluation of Boolean expressions allows a result
without evaluating the second parameter
• Must distinguish between forms that use standard evaluation
(function applications) and those that do not (special forms)
• Inefficient when same delayed expression is repeatedly evaluated
• Scheme uses a memorization process to store the value of the
delayed object the first time it is forced and then return this value
for each subsequent call to force - pass by need

65. Delayed Evaluation
• Runtime rules for lazy evaluation:
▫ All arguments to user-defined functions are delayed
▫ All bindings of local names in Let and Letrec expressions are delayed
▫ All arguments to constructor functions are delayed
▫ All arguments to other predefined functions are forced
▫ All function-valued arguments are forced
▫ All conditions in selection forms are forced
• Lists that obey lazy evaluation may be called streams
• Primary example of a functional language with lazy evaluation is Haskell

66. Anonymous Functions
• Written as lambda abstractions
• The function (x -> x * x) behaves exactly like sqr
▫ sqr x = x * x
▫ sqr 10  100
▫ (x -> x * x) 10  100
• Anonymous functions are first-class values
▫ map (x -> x * x) [1..10]
▫  [1, 4, 9, 16, 25, 36, 49, 64, 81, 100]

67. Currying
• Currying is when you break down a function that takes multiple
arguments into a series of higher-order functions that take part of
the arguments
▫ fname :: (type1, type2) -> type3 =>
▫ fname :: type1 -> type2 -> type3
▫ (+ 2 3) => ((+ 2) 3)

68. Bound and Free variables
• (λx.E)
▫ Scope of binding of lambda is expression E
▫ All occurrences of x in E are bound
▫ All occurrences of x outside E not bound by this lambda
• (λx. + y x)
▫ X bound like a local variable
▫ y is free like a nonlocal reference in the function

69. ILs vs. FPLs
• Imperative Languages
▫ Efficient execution
▫ Complex semantics
▫ Complex syntax
▫ Concurrency is programmer designed
• Functional Languages
▫ Simple semantics
▫ Simple syntax
▫ Inefficient execution
▫ Programs can automatically be made concurrent

70. FPL Issues
• Difficult to implement efficiently on von Neumann machines
• Lots of copying of data through parameters
• Need to create a whole new array in order to change one element
• Heavy use of pointers (space/time and locality problem)
• Frequent procedure calls
• Heavy space use for recursion
• Requires garbage collection
• Requires a different mode of thinking by the programmer
• Difficult to integrate I/O into purely functional model

71. References
1. “Conception, Evolution, and Application of Functional Programming Languages,” Paul Hudak,
ACM Computing Surveys 21/3, 1989, pp 359-411
2. “A Gentle Introduction to Haskell,” Paul Hudak and Joseph H. Fasel www.haskell.org/tutorial/
3. Report on the Programming Language Haskell 98 A Non-strict, Purely Functional Language,
Simon Peyton Jones and John Hughes [editors], February 1999 www.haskell.org
4. Real World Haskell, Bryan O'Sullivan, Don Stewart, and John Goerzen
book.realworldhaskell.org/read/

72. Thank You
Check Out My LinkedIn Profile at
https://in.linkedin.com/in/girishkhanzode