The document introduces principles of programming languages, focusing on modeling computational processes and differentiating between programming paradigms such as functional, logic, and imperative programming. Topics covered include types, semantics, language features, and specific languages like Scheme, ML, and Prolog, along with the mechanics of the Scheme interpreter and evaluation processes. Administrative issues, such as assessment methods and class materials, are also addressed.

1. Principles of
Programming Languages

2. Introduction
• We will study Modeling and Programming Computational Processes
• Design Principles
– Modularity, abstraction, contracts…
• Programming languages features
– Functional Programming
• E.g. Scheme, ML
• Functions are first-class objects
– Logic Programming
• E.g. Prolog
• “Declarative Programming”
– Imperative Programming
• E.g. C,Java, Pascal
• Focuses on change of state
– Not always a crisp distinction – for instance scheme can be used for imperative
programming.

3. 3
Declarative Knowledge
0
and
such that
the
is 2

 y
x
y
y
x
“
What is true
”

4. 4
To find an approximation of x:
• Make a guess G
• Improve the guess by averaging G and x/G
• Keep improving the guess until it is good enough
Imperative and Functional
Knowledge
“
How to
”
An algorithm due to
:
[
Heron of Alexandria
]

5. More topics
• Types
– Type Inference and Type Checking
– Static and Dynamic Typing
• Different Semantics (e.g. Operational)
• Interpreters vs. Compilers
– Lazy and applicative evaluation

6. Languages that will be studied
• Scheme
– Dynamically Typed
– Functions are first-class citizens
– Simple (though lots of parenthesis  )
and allows to show different programming styles
• ML
– Statically typed language
– Polymorphic types
• Prolog
– Declarative, Logic programming language
• Languages are important, but we will focus on the principles

7. Administrative Issues
• Web-site
• Exercises
• Mid-term
• Exam
• Grade

8. Use of Slides
• Slides are teaching-aids, i.e. by nature
incomplete
• Compulsory material include everything
taught in class, practical sessions as well as
compulsory reading if mentioned

9. Today
• Scheme basics
– Syntax and Semantics
– The interpreter
– Expressions, values, types..

10. 10
Scheme
• LISP = LISt Processing
– Invented in 1959 by John McCarthy
– Scheme is a dialect of LISP – invented by Gerry
Sussman and Guy Steele

11. 11
The Scheme Interpreter
• The Read/Evaluate/Print Loop
– Read an expression
– Compute its value
– Print the result
– Repeat the above
• The
(Global) Environment
– Mapping of names to values
score 23
total 25
percentage 92
Name Value

12. 12
Language Elements
Means of
Abstraction
(define score 23) Associates score with
23 in environment
table
Syntax Semantics
Means of
Combination
(composites)
(+ 3 17 5) Application of proc to
arguments
Result = 25
Primitives 23
+
*
#t, #f
23
Primitive Proc (add)
Primitive Proc (mult)
Boolean

13. 13
Computing in Scheme
>==
23
23
+( >==
3
17
5
)
25
+( >==
3
*(
5
6
)
8
2
)
43
( >==
define score 23
)
Name Value
Environment Table
23
score
Opening parenthesis
Expression whose
value is a procedure
Other expressions
Closing parenthesis

14. 14
Computing in Scheme
>==
score
23
( >==
define total 25
)
*( >==
100
/(
score total
))
92
( >==
define percentage (* 100 (/ score total))
Name Value
Environment
23
score
25
total
92
percentage
>==
Atomic (can’t decompose) but not primitive
A name-value pair in the env. is called binding

15. 15
Evaluation of Expressions
To Evaluate a combination: (as opposed to special form)
a. Evaluate all of the sub-expressions in some order
b. Apply the procedure that is the value of the leftmost
sub-expression to the arguments (the values of the other
sub-expressions)
The value of a numeral: number
The value of a built-in operator: machine instructions to execute
The value of any name: the associated value in the environment

16. 16
Using Evaluation Rules
( >==
define score 23
)
+( *( >==
5
6
-( )
score (* 2 3 2 )
))
Special Form (second sub-
expression is not evaluated)
* + 5 6
11
- 23 * 3 2
2
12
11
121

17. 17
Abstraction – Compound Procedures
•
How does one describe procedures
?
•
(
lambda (x) (* x x)
)
To process something multiply it by itself
formal parameters
body
Internal representation
• Special form – creates a “procedure object” and
returns it as a “value”
Proc (x) (* x x)

18. 18
More on lambdas
• The use of the word “lambda” is taken from lambda
calculus.
• A lambda body can consist of a sequence of
expressions
• The value returned is the value of the last one
• So why have multiple expressions at all?

19. 19
Evaluation of An Expression
To Apply a compound procedure: (to a list of arguments)
Evaluate the body of the procedure with the formal parameters
replaced by the corresponding actual values
(( >==
lambda(x)(* x x)
)
5
)
Proc(x)(* x x) 5
*(
5
5
)
25

20. 20
Evaluation of An Expression
To Apply a compound procedure: (to a list of arguments)
Evaluate the body of the procedure with the formal parameters
replaced by the corresponding actual values
To Evaluate a combination: (other than special form)
.a
Evaluate all of the sub-expressions in any order
.b
Apply the procedure that is the value of the leftmost sub-expression to the
arguments (the values of the other sub-expressions)
The value of a numeral: number
The value of a built-in operator: machine instructions to execute
The value of any name: the associated object in the environment

21. 21
Using Abstractions
( >==
square 3
)
9
( +( >==
square 3
( )
square 4
))
( >==
define square (lambda(x)(* x x))
)
*(
3
3
*( )
4
4
)
9 16
+
25
Environment Table
Name Value
square Proc (x)(* x x)

22. 22
Yet More Abstractions
==> (define f
(lambda(a)
(sum-of-two-squares (+ a 3) (* a 3))))
( >==
sum-of-two-squares 3 4
)
25
==> (define sum-of-two-squares
(lambda(x y)(+ (square x) (square y))))
Try it out…compute (f 3) on your own

23. 23
Evaluation of An Expression (reminder)
To Apply a compound procedure: (to a list of arguments)
Evaluate the body of the procedure with the formal parameters
substituted by the corresponding actual values
To Evaluate a combination: (other than special form)
.a
Evaluate all of the sub-expressions in any order
.b
Apply the procedure that is the value of the leftmost sub-expression to the
arguments (the values of the other sub-expressions)
The value of a numeral: number
The value of a built-in operator: machine instructions to execute
The value of any name: the associated object in the environment

24. 24
Lets not forget The Environment
( >==
define x 8
)
+( >==
x 1
)
9
( >==
define x 5
)
+( >==
x 1
)
6
The value of (+ x 1) depends
on the environment
!

25. 25
Using the substitution model
(
define square (lambda (x) (* x x))
)
(
define average (lambda (x y) (/ (+ x y) 2))
)
(
average 5 (square 3)
)
(
average 5 (* 3 3)
)
(
average 5 9
)
first evaluate operands,
then substitute
+( /(
5
9
)
2
)
/(
14
2
)
if operator is a primitive procedure,
7
replace by result of operation

26. 26
Booleans
Two distinguished values denoted by the constants
#
t and #f
The type of these values is boolean
<( >==
2
3
)
#
t
<( >==
4
3
)
#
f

27. Values and types
Values have types. For example
:
In scheme almost every expression has a value
Examples:
1) The value of 23 is 23
2) The value of + is a primitive procedure for addition
3) The value of (lambda (x) (* x x)) is the compound
procedure proc(x) (* x x) (also denoted <Closure (x) (* x
x)>
1) The type of 23 is numeral
2) The type of + is a primitive procedure
3) The type of proc (x) (* x x) is a compound procedure
4) The type of (> x 1) is a boolean (or logical)

28. Atomic and Compound Types
• Atomic types
– Numbers, Booleans, Symbols (TBD)
• Composite types
– Types composed of other types
– So far: only procedures
– We will see others later

29. 29
No Value
?
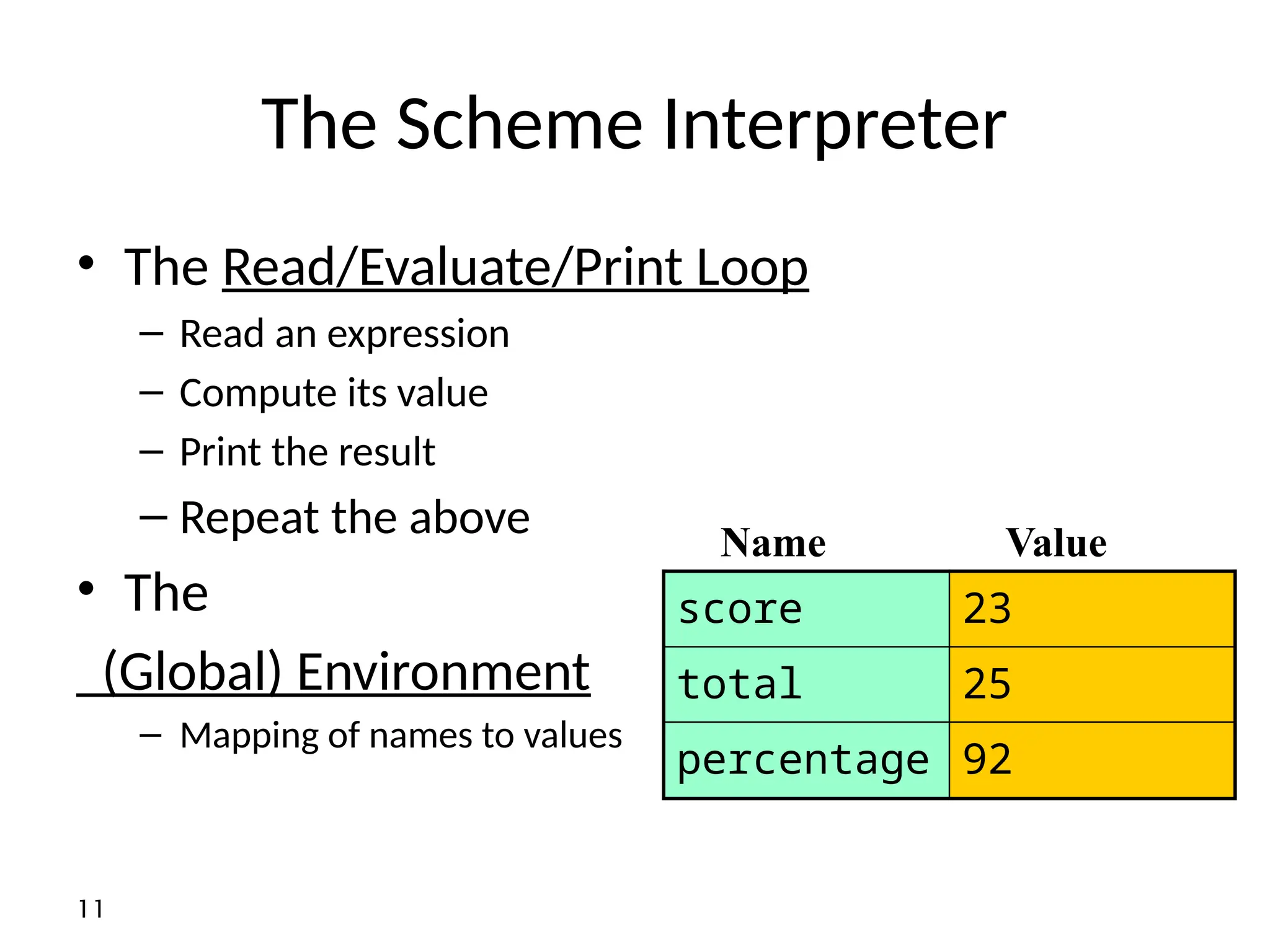
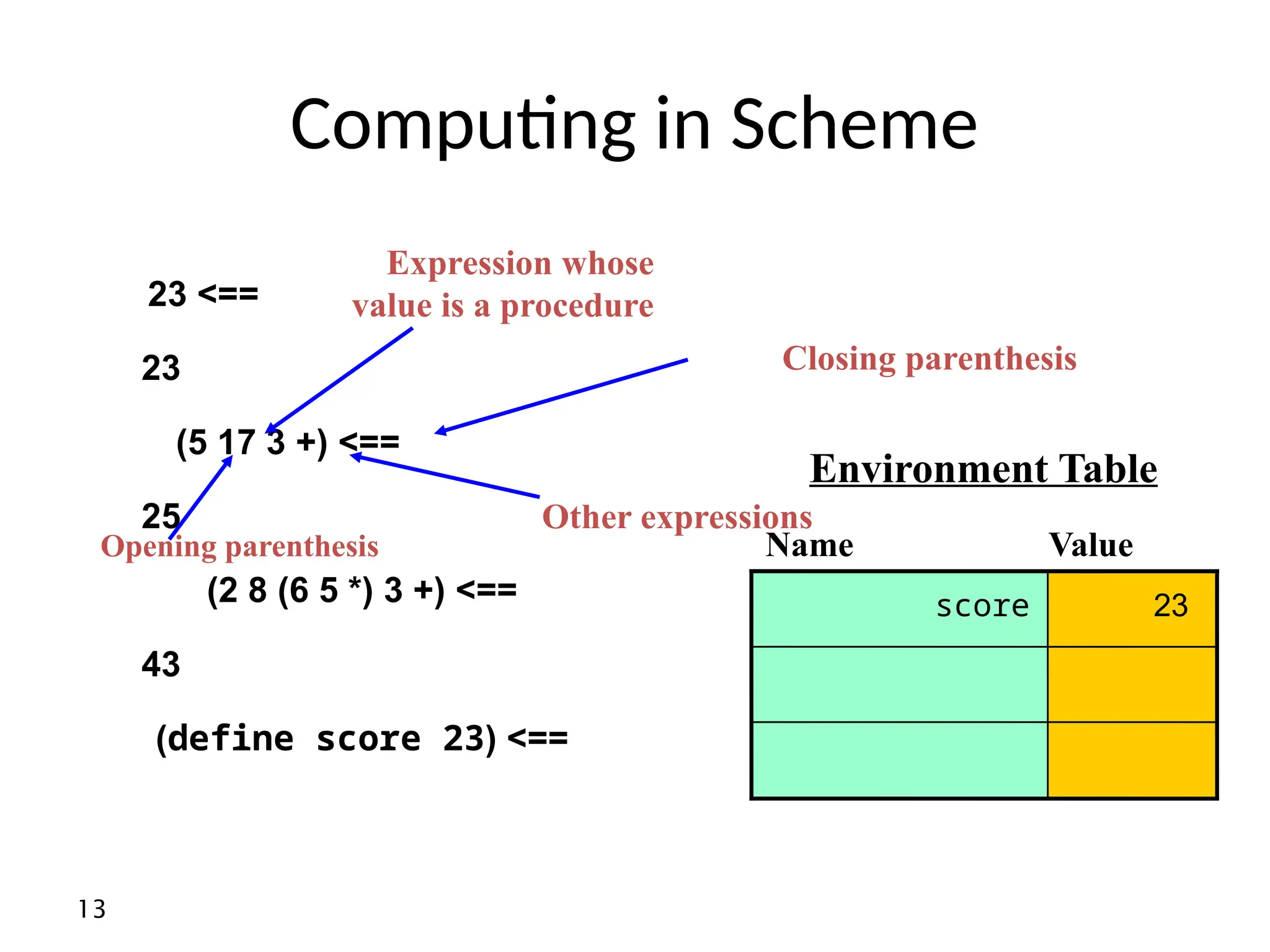
• In scheme most expressions have values
• Not all! Those that don’t usually have side effects
Example : what is the value of the expression
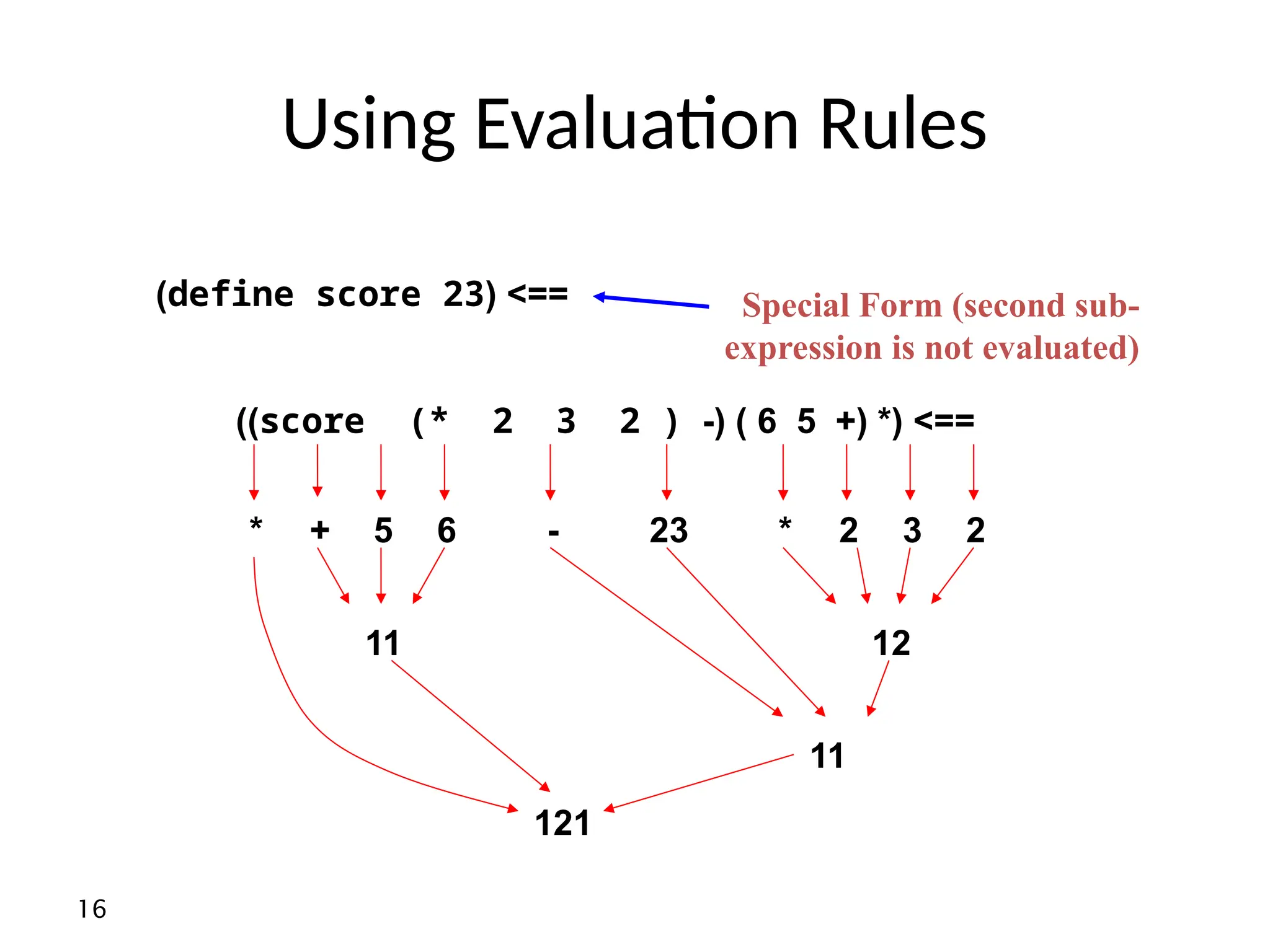
(define x 8)
And of
(display x)
[display is a primitive func., prints the value of its
argument to the screen]
• In scheme, the value of a define, display expression is
“undefined” . This means “implementation-dependent”
• Never write code that relies on such value!

30. Dynamic Typing
• Note that we never specify explicitly types of
variables
• However primitive functions expect values of a
certain type!
– E.g. “+” expects numeral values
• So will our procedures (To be discussed soon)
• The Scheme interpreter checks type correctness
at run-time: dynamic typing
– [As opposed to static typing verified by a compiler ]

31. 31
More examples
( >==
define x 8
)
Name Value
Environment Table
8
x
( >==
define x (* x 2)
)
>==
x
16
16
( >==
define x y
)
reference to undefined identifier: y
( >==
define
)- +
>-<#
+
+( >==
2
2
)
0
Bad practice, disalowed by some interpreters

32. The IF special form
ERROR
2
(
if <predicate> <consequent> <alternative
)>
If the value of <predicate> is #t,
Evaluate <consequent> and return it
Otherwise
Evaluate <alternative> and return it
(
if (< 2 3) 2 3
>== )
2
(
if (< 2 3) 2 (/ 1 0)
>== )

33. IF is a special form
• In a general form, we first evaluate all arguments and then
apply the function
• (if <predicate> <consequent> <alternative>)
is different:
<predicate> determines whether we evaluate
<consequent> or <alternative>.
We evaluate only one of them !

34. Conditionals
(lambda (a b)
(cond ( (> a b) a)
( (< a b) b)
(else -1 )))

35. Syntactic Sugar for naming procedures
(
define square (lambda (x) (* x x))
(
define (square x) (* x x)
)
Instead of writing
:
We can write:

36. (
define second
)
(
second 2 15 3
>== )
15
(
second 34 -5 16
- >== )
5
Some examples
:
(
lambda (x) (* 2 x)
)
(
lambda (x y z) y
)
Using “syntactic sugar
:”
(
define (twice x) (* 2 x)
)
Using “syntactic sugar
:”
(
define (second x y z) y
)
(define twice )
(twice 2) ==> 4
(twice 3) ==> 6

37. Symbols
> (quote a)
a
> ’a
a
> (define a ’a)
> a
a
> b
a
> (define b a)
> (eq? a b)
#t
> (symbol? a)
#t
> (define c 1)
> (symbol? c)
#f
> (number? c)
#t
Symbols are atomic
types, their values
unbreakable
:
‘
abc is just a symbol

38. More on Types
• A procedure type is a composite type, as it is
composed of the types of its inputs (domain)
and output (range)
• In fact, the procedure type can be instantiated
with any type for domain and range, resulting
in a different type for the procedure (=data)
• Such types are called polymorphic
– Another polymorphic type: arrays of values of type
X (e.g. STL vectors in C++)

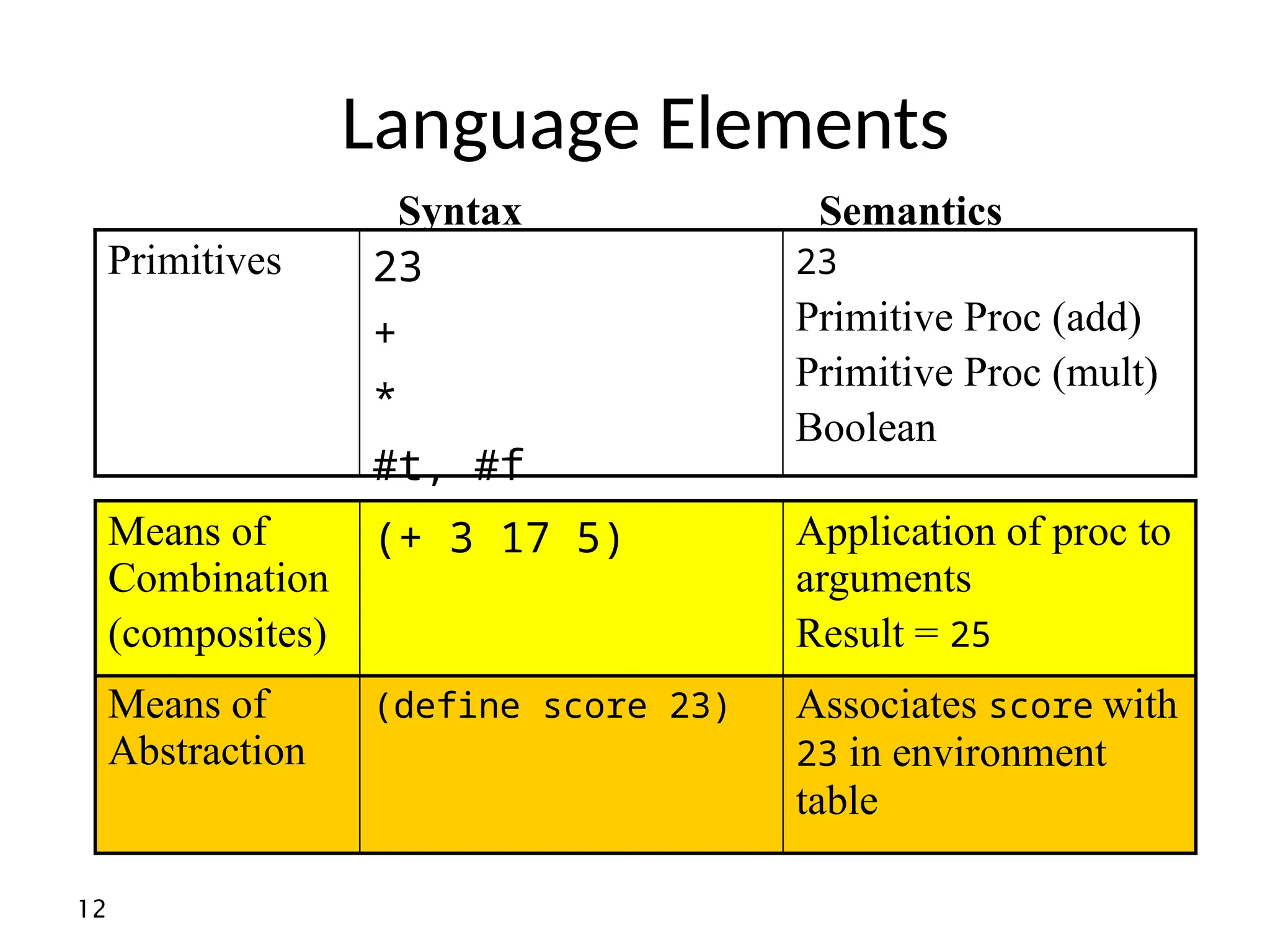
39. Type constructor
• Defines a composite type out of other types
• The type constructor for functions is denoted “->”
• Example: [Number X Number –> Number] is the type of all procedures
that get as input two numbers, and return a number
• If all types are allowed we use a type variable:
– [T –> T] is the type of all procs. That return the same type as they get as input
• Note: there is nothing in the syntax for defining types! This is a
convention we manually enforce (for now..).

40. Scheme Type Grammar
Type --> ’Unit’ | Non-Unit [Unit=Void]
Non-unit -> Atomic | Composite | Type-variable
Atomic --> ’Number’ | ’Boolean’ | ’Symbol’
Composite --> Procedure | Union
Procedure --> ’Unit ’->’ Type | ’[’ (Non-Unit ’*’)* Non-
Unit ’->’ Type ’]’
Union --> Type ’union’ Type
Type-variable -> A symbol starting with an upper case
letter

41. Value constructor
• Means of defining an instance of a particular
type.
• The value constructors for procedures is
lambda
– Each lambda expression generates a new
procedure