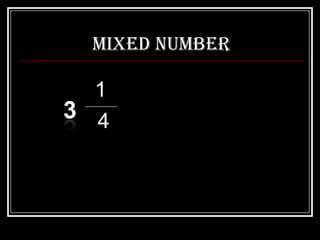This document provides information about fractions, including definitions and classifications. It defines a fraction as the quotient of two rational numbers, and classifies fractions as proper, improper, or mixed numbers. It also discusses equivalent fractions, ordering fractions with like and unlike denominators using common denominators, and methods for finding the least common multiple (LCM) of denominators.

1. Understanding
Fractions

2. Fraction
o A fraction is the quotient of two rational numbers.
Numerator
Denominator

3. Classification of Fractions
Proper Fraction
 Improper Fraction
 Mixed Number

4. Classification of Fractions
 A proper fraction is a fraction with the
numerator less (smaller) than the
denominator.
 An improper fraction is a fraction with the
numerator great (larger) than or equal (the
same) to the denominator.
 A mixed number has a fraction and a whole
number.

5. Proper Fractions
3 1
4 2

6. Improper Fractions
7 9
5 9

7. Mixed Number
1
4

8. Equivalent Fractions
equivalent fractions are fractions that
have different denominators, but are the
same size.
These are equivalent fractions.
6 1
18 3

9. Ordering Fractions
 To order fractions with like denominators:
 First look at the numerators.
 Place the fractions with the lowest numerator
first.
 Place the second lowest numerator next.
 Keep doing this until there are no more fractions.

10. Ordering Fractions
 Order the following fractions:
2 1 3
4 4 4
 The answer:
1 2 3
4 4 4

11. Ordering Fractions
To order fractions with unlike denominators.
First, find a common denominator, which is the
smallest whole number that is divisible by each of the
denominators.
You find a common denominator by finding the Least
Common Multiple (LCM) for those numbers.

12. Least Common Multiple (LCM)
Method 1
List the multiples of each denominator (multiply by
2, 3, 4, etc.) then look for the smallest common number in
each list.
Example
1/5, 1/6, and 1/15
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 45
Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48
Multiples of 15: 15, 30, 45

13. LCM
 The LCM of 5, 6, and 15 is 30; so the common
denominator would be 30.
x6 =
x6 =
 You continue with the other two fractions.

14. Ordering Fractions
Now that you have a common denominator. You
put the fractions in order from Least to Greatest.
6 5 2 2 5 6
30 30 30 30 30 30

15. LCM
Method 2:
• Factor each of the denominators into primes.
• Then count the number of times each prime number appears in
the factorizations.
•For each prime number, take the largest of these counts. Write
down that prime number as many times as you counted.
• The product of all the prime numbers written down is the least
common denominator.

16. Method 2
o Factor each of the numbers into primes.
o Count the number of times each prime number appears in the
factorizations.
o For each prime number, take the largest of these counts.
o Write down that prime number as many times as you counted
for it in step 2.
o The least common multiple is the product of all the prime
numbers written down.

17. Method 2
Example: Find the LCM of 5, 6, and 15
• Prime factorization of 5 is 5
• Prime factorization of 6 is 2 x 3
• Prime factorization of 15 is 3 x 5
• The LCM of 5, 6. & 15 is: 5 x 2 x 3; which = 30

18. Method 2
o The largest count of 2s is one
o The largest count of 3s is one
o The largest count of 5s is one
o So, we simply take 2 x 3 x 5 = 30
o Therefore, 30 is the LCM of 5, 6, and 15.