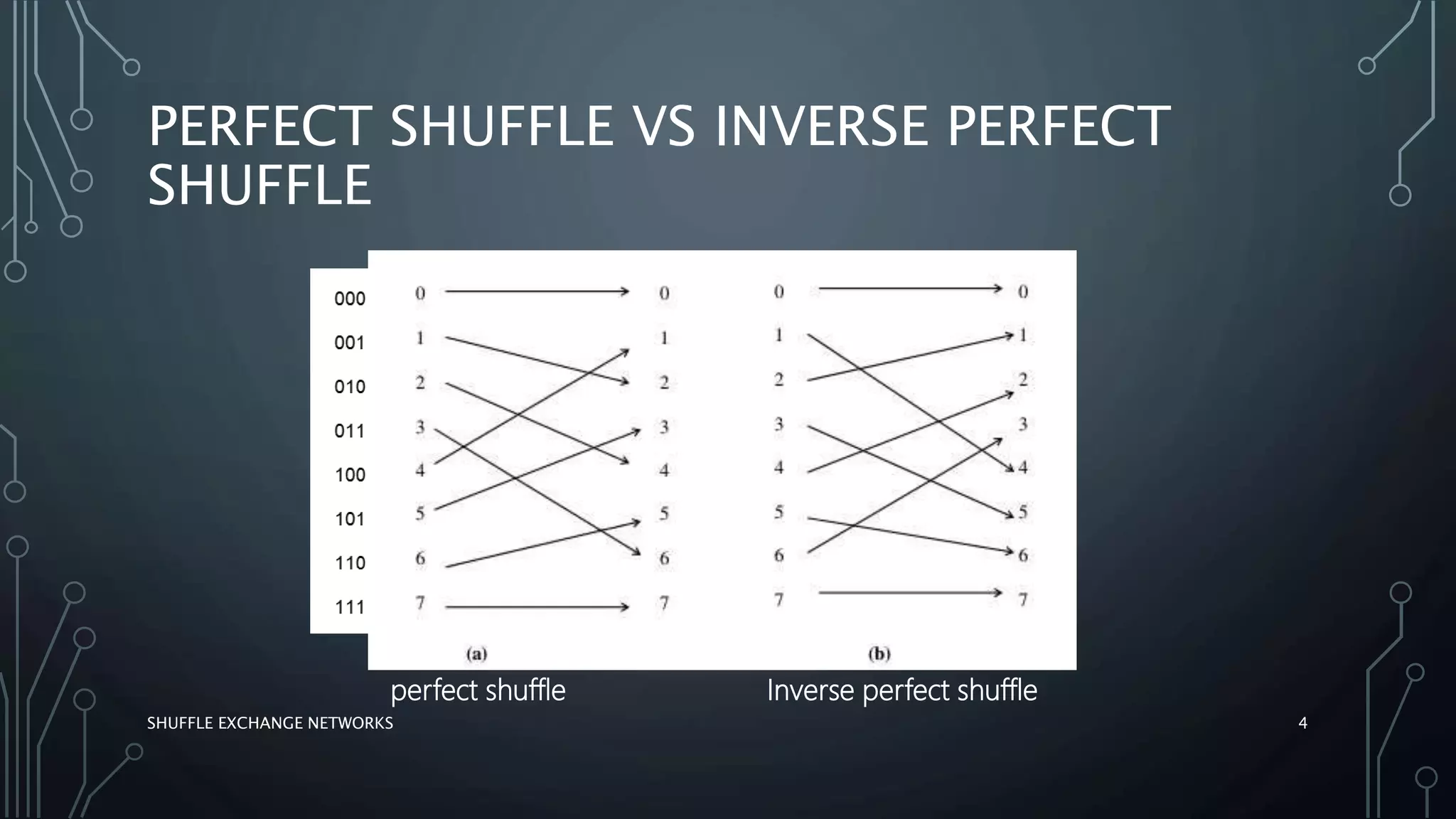
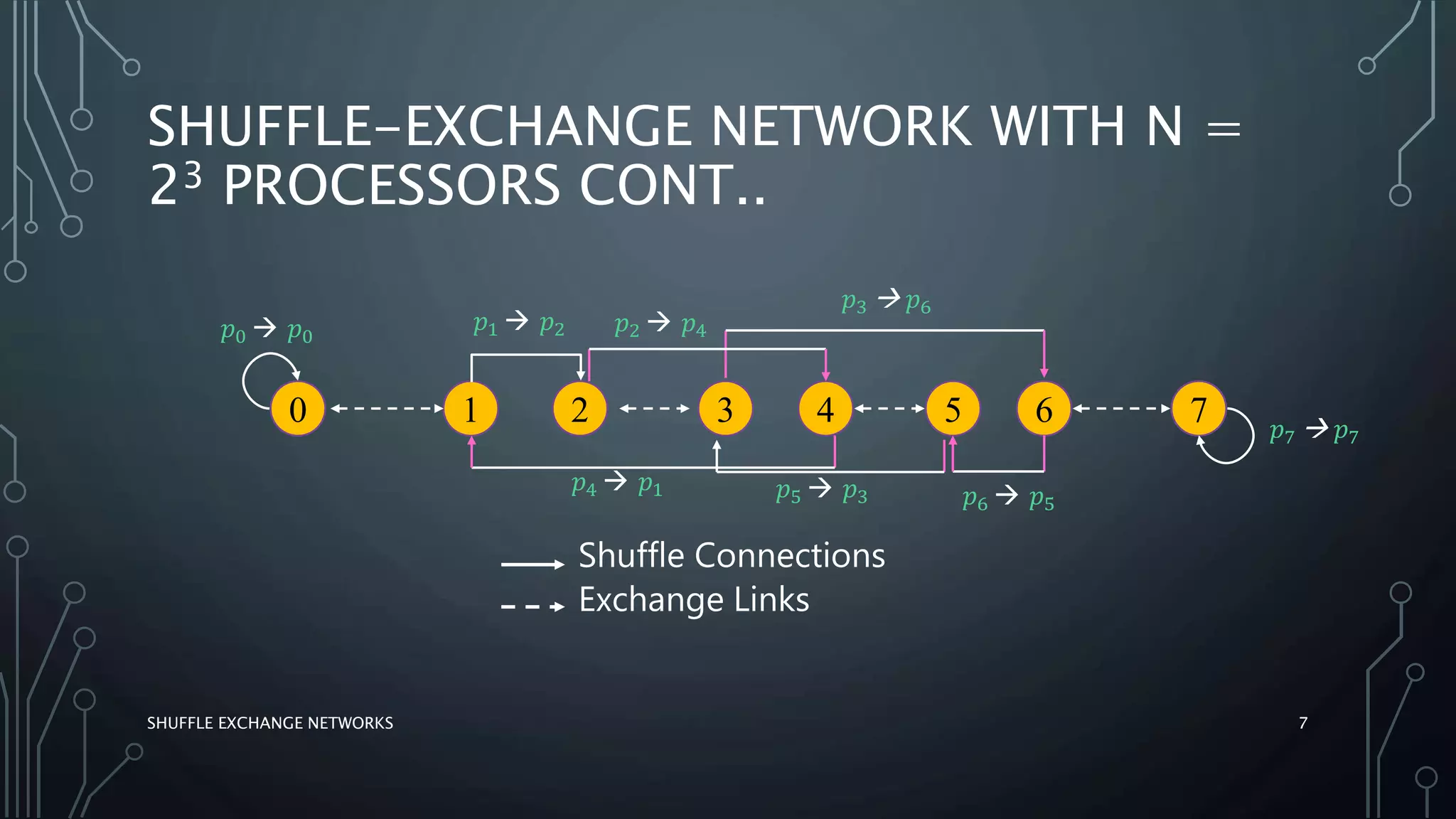
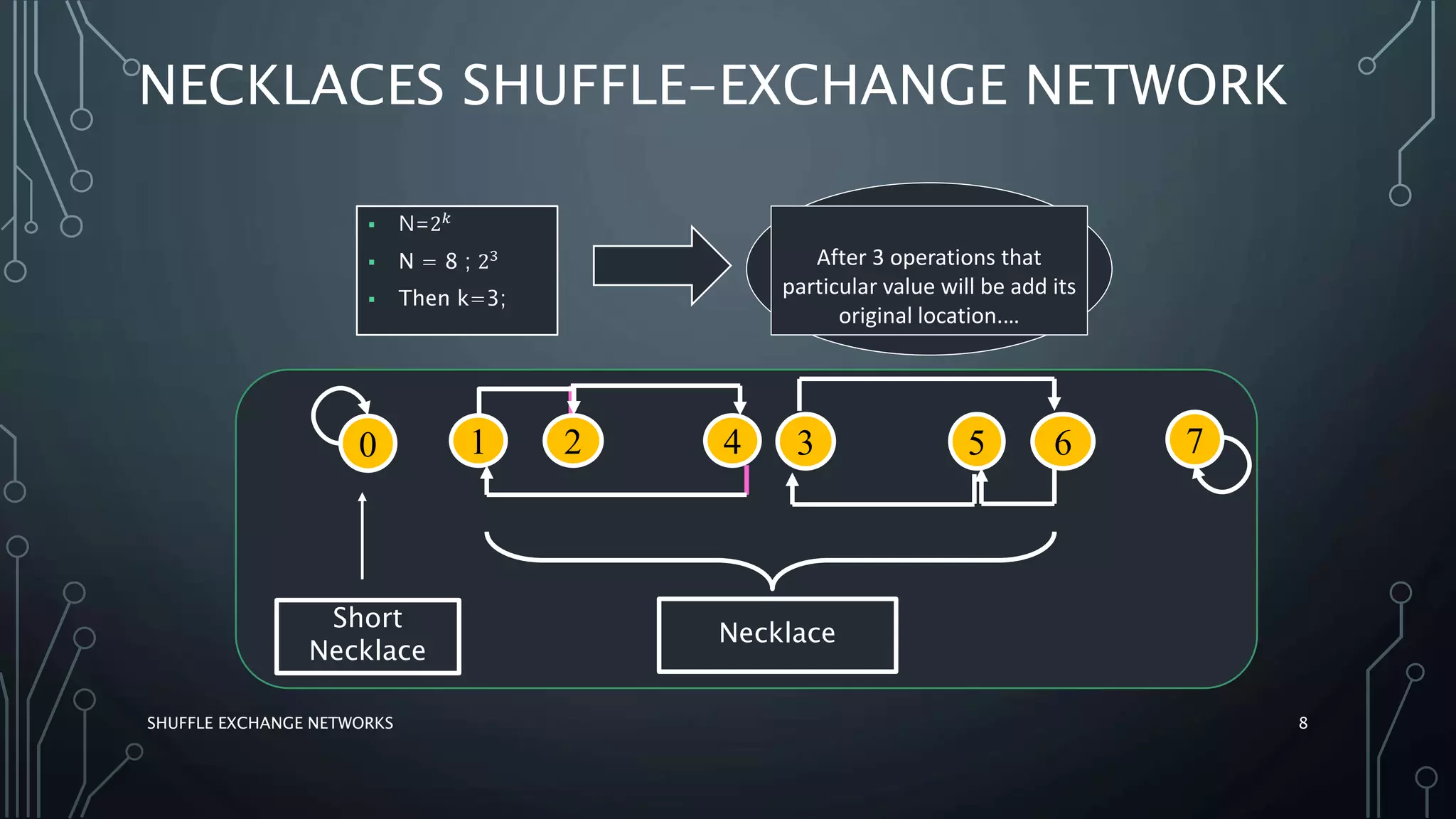
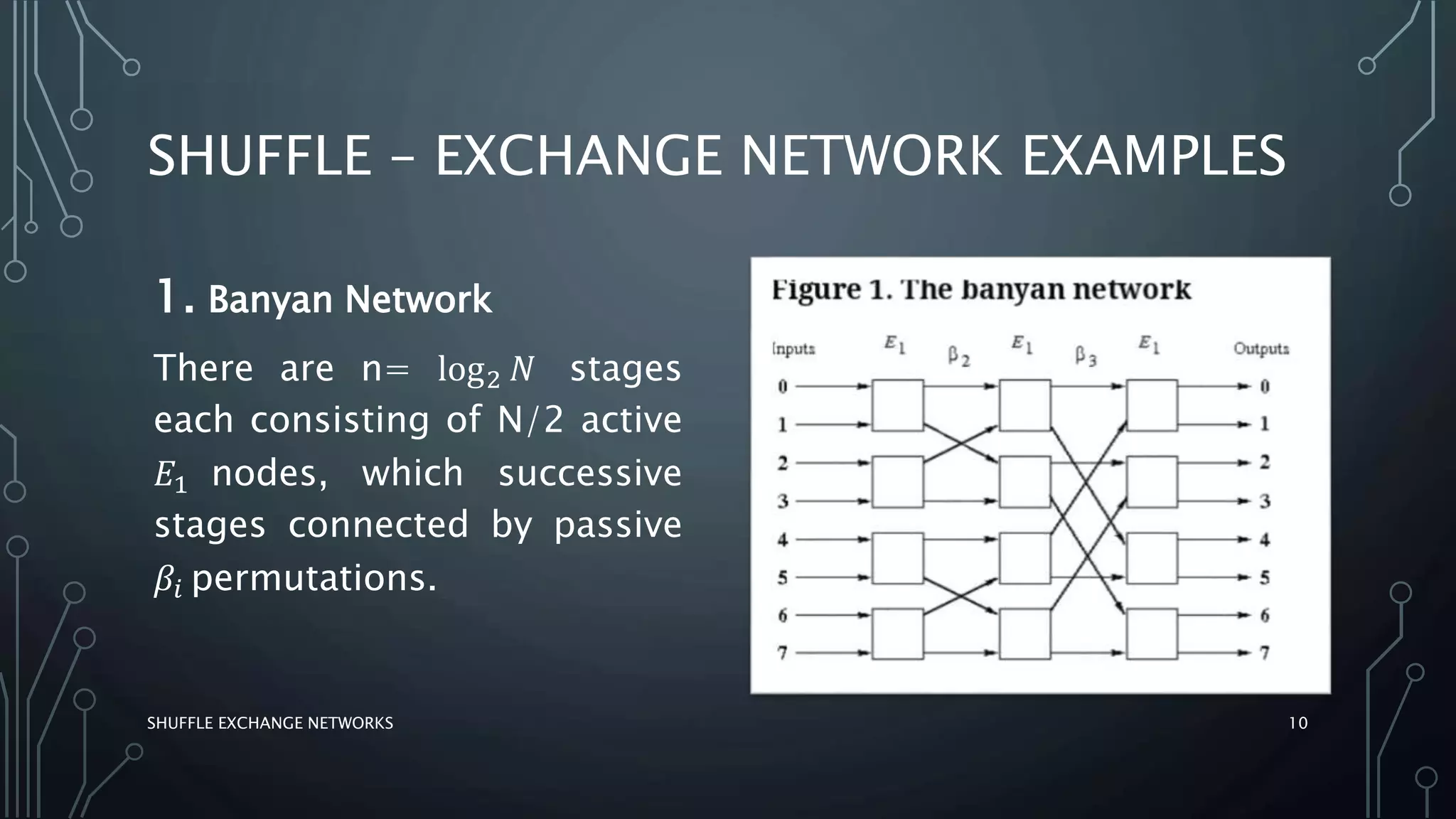
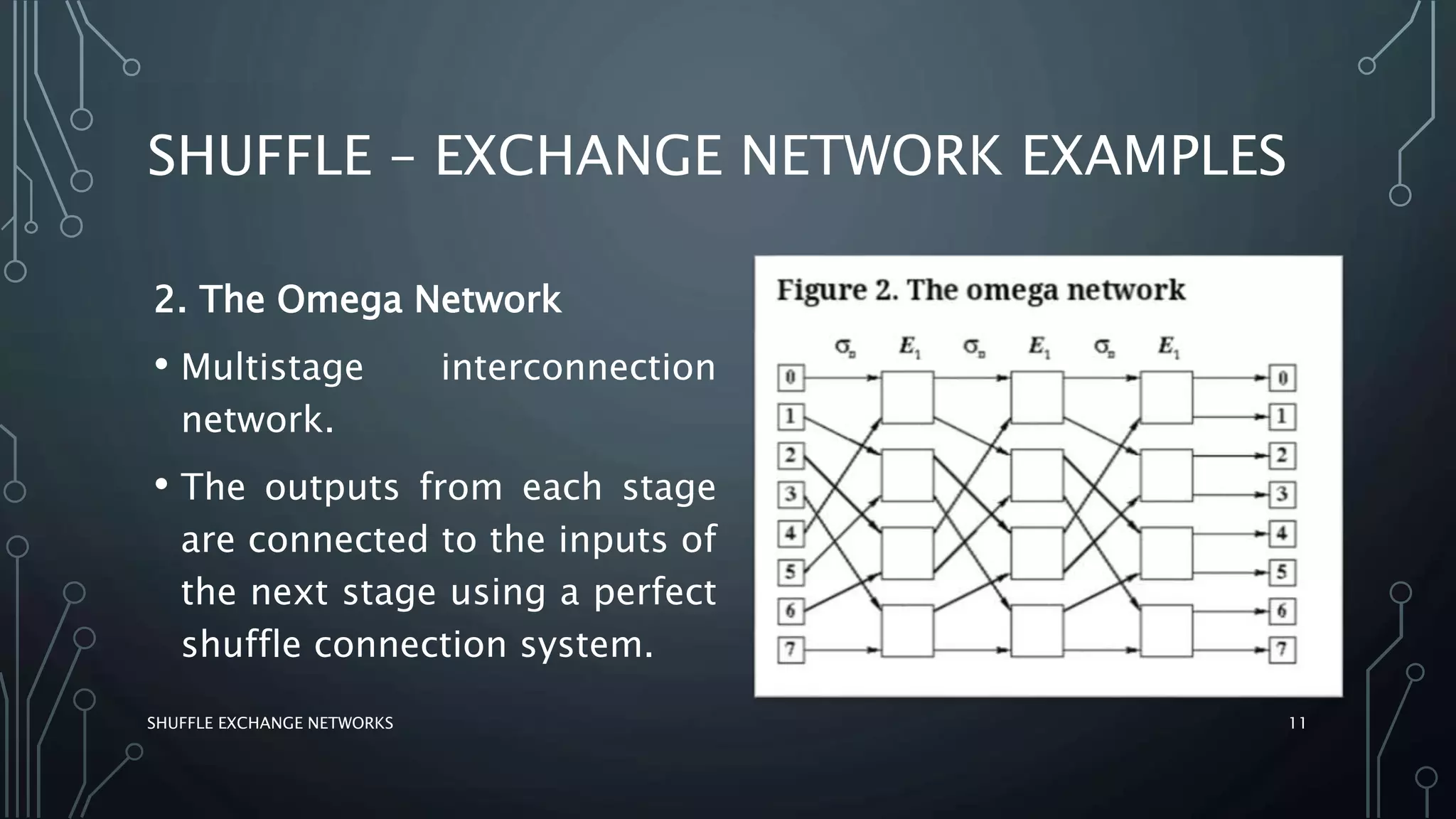
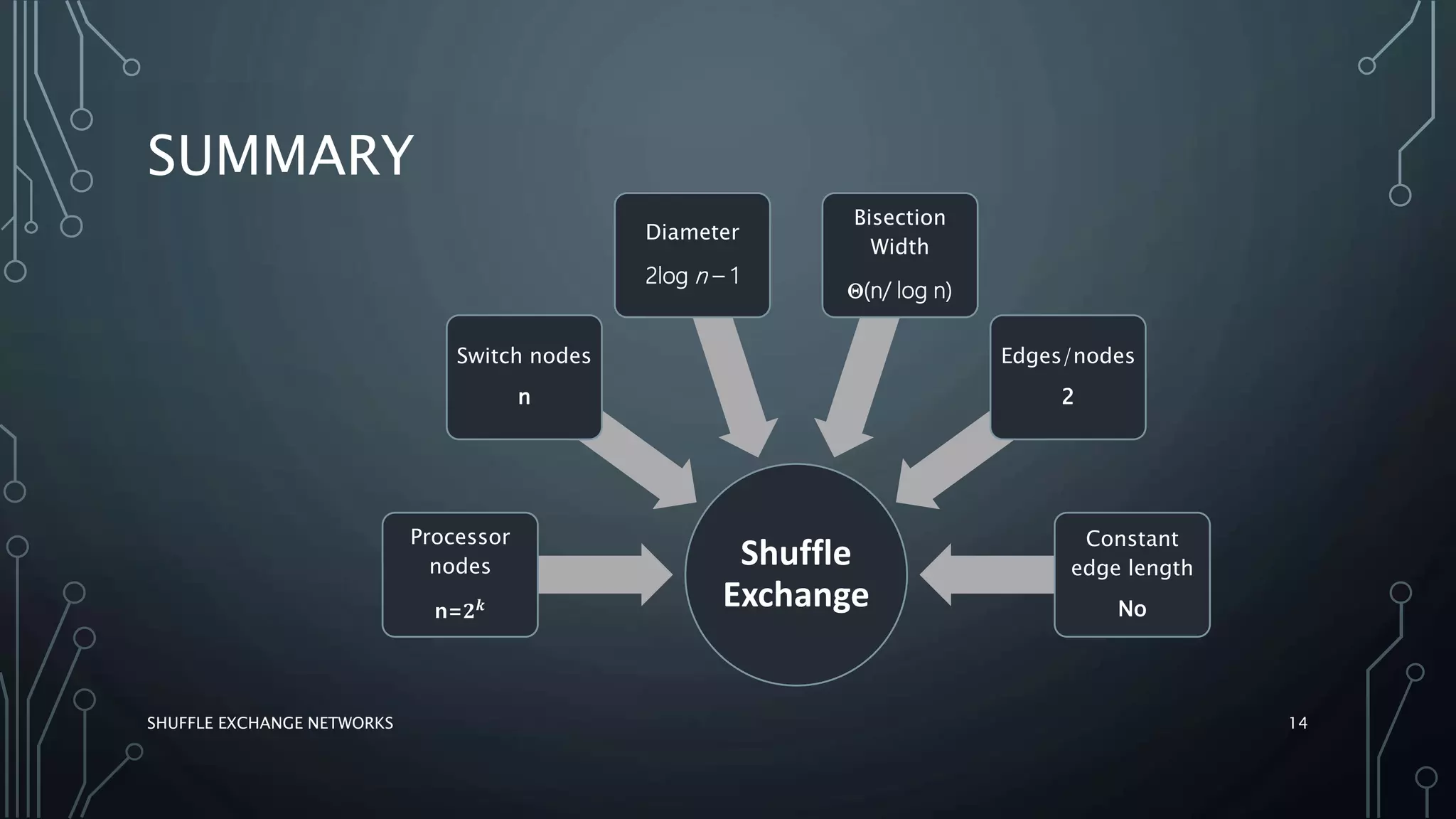
The document discusses shuffle exchange networks (SEN), which facilitate multistage interconnection through unique paths between inputs and outputs, particularly suited for parallel algorithms. It covers the concepts of perfect and inverse perfect shuffles, implementation examples, and applications such as polynomial evaluation and Fast Fourier Transform. Additionally, it highlights challenges faced by larger networks, including traffic hotspots and decomposition issues.

1. SHUFFLE EXCHANGE
NETWORKS
A G A L DANUSHKA - SEU/IS/14/PS/101 - PS0722

2. CONTENT
• Introduction
• Perfect Shuffle Vs Inverse Perfect Shuffle
• Perfect Shuffle Interconnection Network
• Perfect Shuffle Implementation
• Examples
• Applications
• Problems
• Summary
2SHUFFLE EXCHANGE NETWORKS

3. INTRODUCTION
• Shuffle Exchange Network (SEN) is a unique path it has only a single
path between a particular input and output.
• These networks are frequently applied with simple modular switches,
make use of two input and two output switching elements.
• Shuffle exchange network suitable in multistage interconnection
network architecture because it can provide an alternative path for
routing procedure.
3SHUFFLE EXCHANGE NETWORKS

4. PERFECT SHUFFLE VS INVERSE PERFECT
SHUFFLE
perfect shuffle Inverse perfect shuffle
4SHUFFLE EXCHANGE NETWORKS

5. PERFECT SHUFFLE INTERCONNECTION
NETWORK
 Let N; no. of processors where; 𝑝0 , 𝑝1 , 𝑝 𝑁−1
 N is power of 2
 There are one way link between each pair of processors
𝑝𝑖 to 𝑝𝑗 ; where
2𝑖 𝑓𝑜𝑟 0 ≤ 𝑖 ≤
𝑁
2
− 1
2𝑖 + 1 − 𝑁 𝑓𝑜𝑟
𝑁
2
≤ 𝑖 ≤ 𝑁 − 1
(Basic permutation for the perfect shuffle network.)
j =
5SHUFFLE EXCHANGE NETWORKS

6. SHUFFLE-EXCHANGE NETWORK WITH N =
23 PROCESSORS
6SHUFFLE EXCHANGE NETWORKS
2𝑖 𝑓𝑜𝑟 0 ≤ 𝑖 ≤
𝑁
2
− 1
2𝑖 + 1 − 𝑁 𝑓𝑜𝑟
𝑁
2
≤ 𝑖 ≤ 𝑁 − 1
Solving the equation for N=8
j =
j= 2i for 0 ≤ i ≤ 3
j= 2i-7 for 4 ≤ i ≤ 7
For i=0 to 3 ; (𝑝0 , 𝑝1 , 𝑝2, 𝑝3 ;
𝑝 − 𝑝𝑟𝑜𝑐𝑒𝑠𝑠𝑜𝑟)
Links will be
• i=0  2i  0
• i=1  2i  2
• i=2  2i  4
• i=3  2i  6
𝑝0  𝑝0
𝑝1  𝑝2
𝑝2  𝑝4
𝑝3  𝑝6
For i=4 to 7 ; (𝑝4 , 𝑝5 , 𝑝6, 𝑝7 )
Links will be
• i=4  2i-7  1
• i=5  2i-7  3
• i=6  2i-7  5
• i=7  2i-7  7
𝑝4  𝑝1
𝑝5  𝑝3
𝑝6  𝑝5
𝑝7  𝑝7
Therefore the range is 0 to 7

7. SHUFFLE-EXCHANGE NETWORK WITH N =
23 PROCESSORS CONT..
SHUFFLE EXCHANGE NETWORKS 7
Shuffle Connections
Exchange Links
0 1 2 3 4 5 6 7
𝑝0  𝑝0
𝑝1  𝑝2 𝑝2  𝑝4
𝑝3  𝑝6
𝑝4  𝑝1 𝑝5  𝑝3 𝑝6  𝑝5
𝑝7  𝑝7

8. SHUFFLE EXCHANGE NETWORKS 8
 N=2 𝑘
 N = 8 ; 23
 Then k=3;
After 3 operations that
particular value will be add its
original location.…
1 2 4 3 5 6
Necklace
Short
Necklace
0 7
NECKLACES SHUFFLE-EXCHANGE NETWORK

9. IMPLEMENTATION OF PERFECT SHUFFLE
SHUFFLE EXCHANGE NETWORKS 9
01. Define a array of length
n and initialize processor
numbers
02. Shuffle First Half
03. Shuffle Second Half

10. SHUFFLE – EXCHANGE NETWORK EXAMPLES
1. Banyan Network
There are n= log2 𝑁 stages
each consisting of N/2 active
𝐸1 nodes, which successive
stages connected by passive
𝛽𝑖 permutations.
SHUFFLE EXCHANGE NETWORKS 10

11. SHUFFLE – EXCHANGE NETWORK EXAMPLES
2. The Omega Network
• Multistage interconnection
network.
• The outputs from each stage
are connected to the inputs of
the next stage using a perfect
shuffle connection system.
SHUFFLE EXCHANGE NETWORKS 11

12. SHUFFLE EXCHANGE NETWORK
APPLICATIONS
Shuffle exchange network provides suitable interconnection
patterns for implementing certain parallel algorithms such as;
SHUFFLE EXCHANGE NETWORKS 12
• Polynomial evaluation
• Fast Fourier Transform(FFT)
• Sorting
• Matrix transposition

13. PROBLEMS WITH SHUFFLE EXCHANGE
SHUFFLE EXCHANGE NETWORKS 13
• A large shuffle-exchange network does not decompose well
into smaller separate shuffle exchange networks.
• In a large shuffle-exchange network, a small percentage of
nodes will be hot spots
• They will encounter much heavier traffic

14. SUMMARY
14SHUFFLE EXCHANGE NETWORKS
Shuffle
Exchange
Processor
nodes
n=𝟐 𝒌
Switch nodes
n
Diameter
2log n – 1
Bisection
Width
(n/ log n)
Edges/nodes
2
Constant
edge length
No

15. THANK
YOU
15SHUFFLE EXCHANGE NETWORKS

16. QUESTIONS
?
16SHUFFLE EXCHANGE NETWORKS