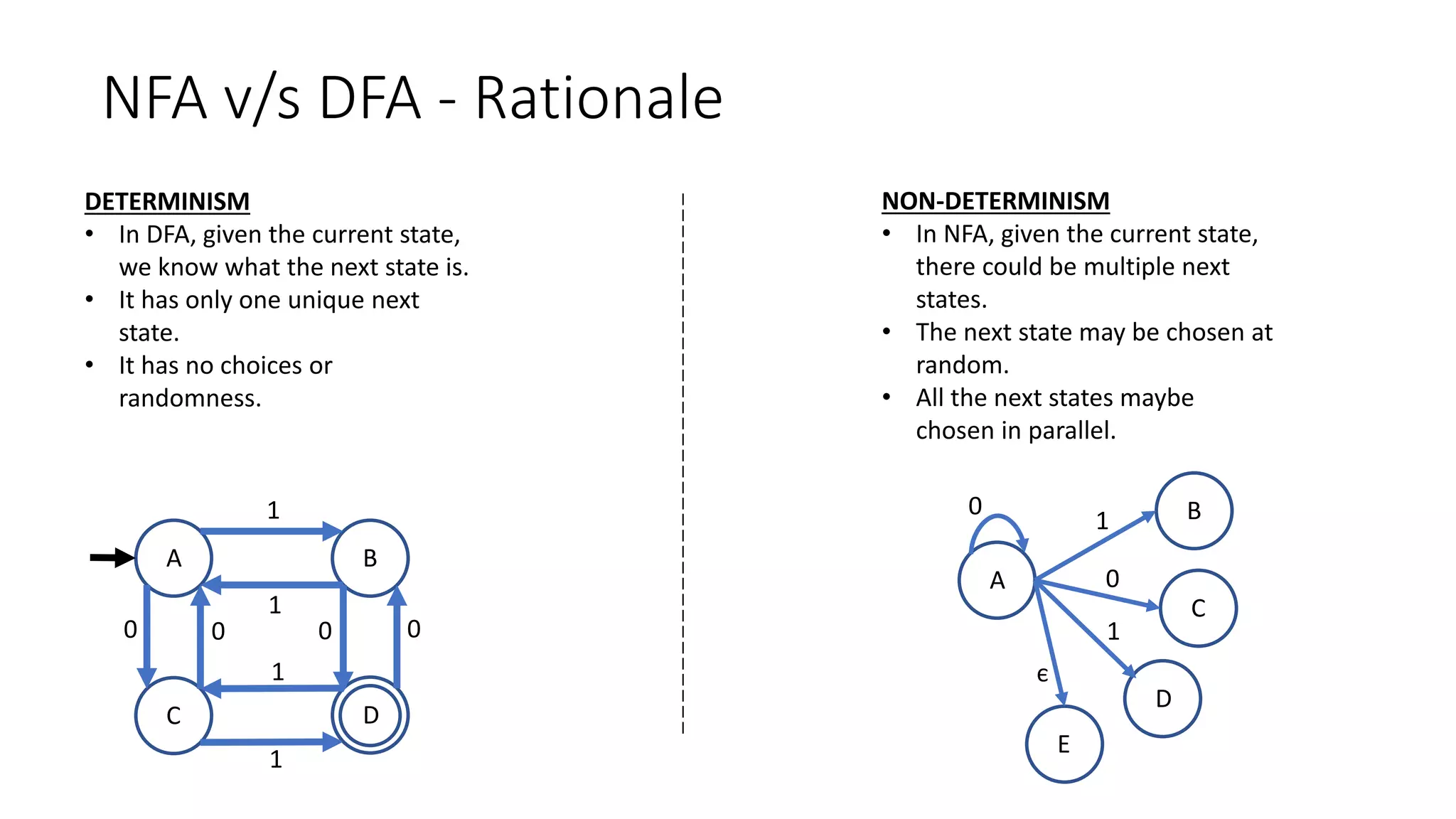
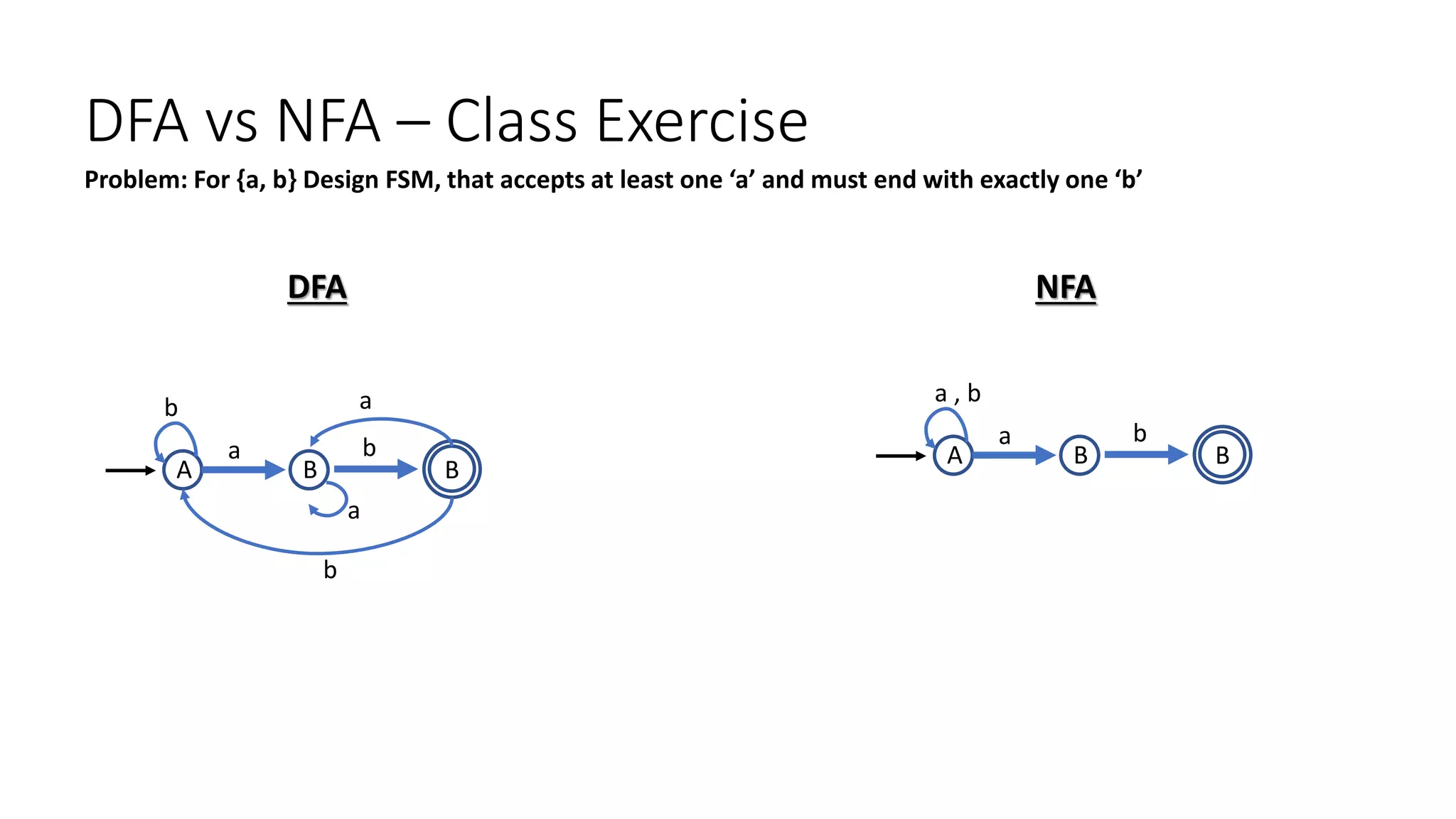
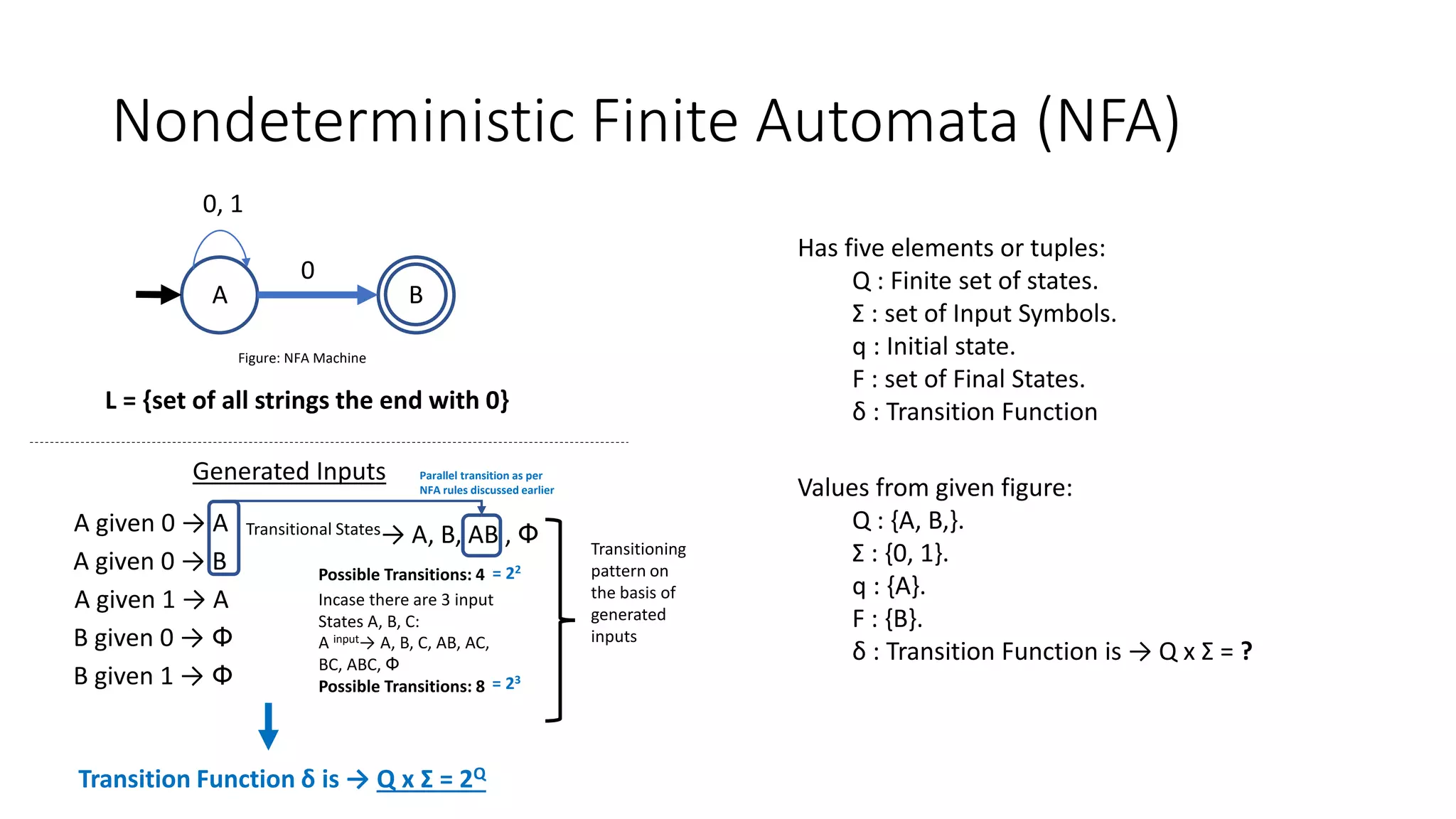
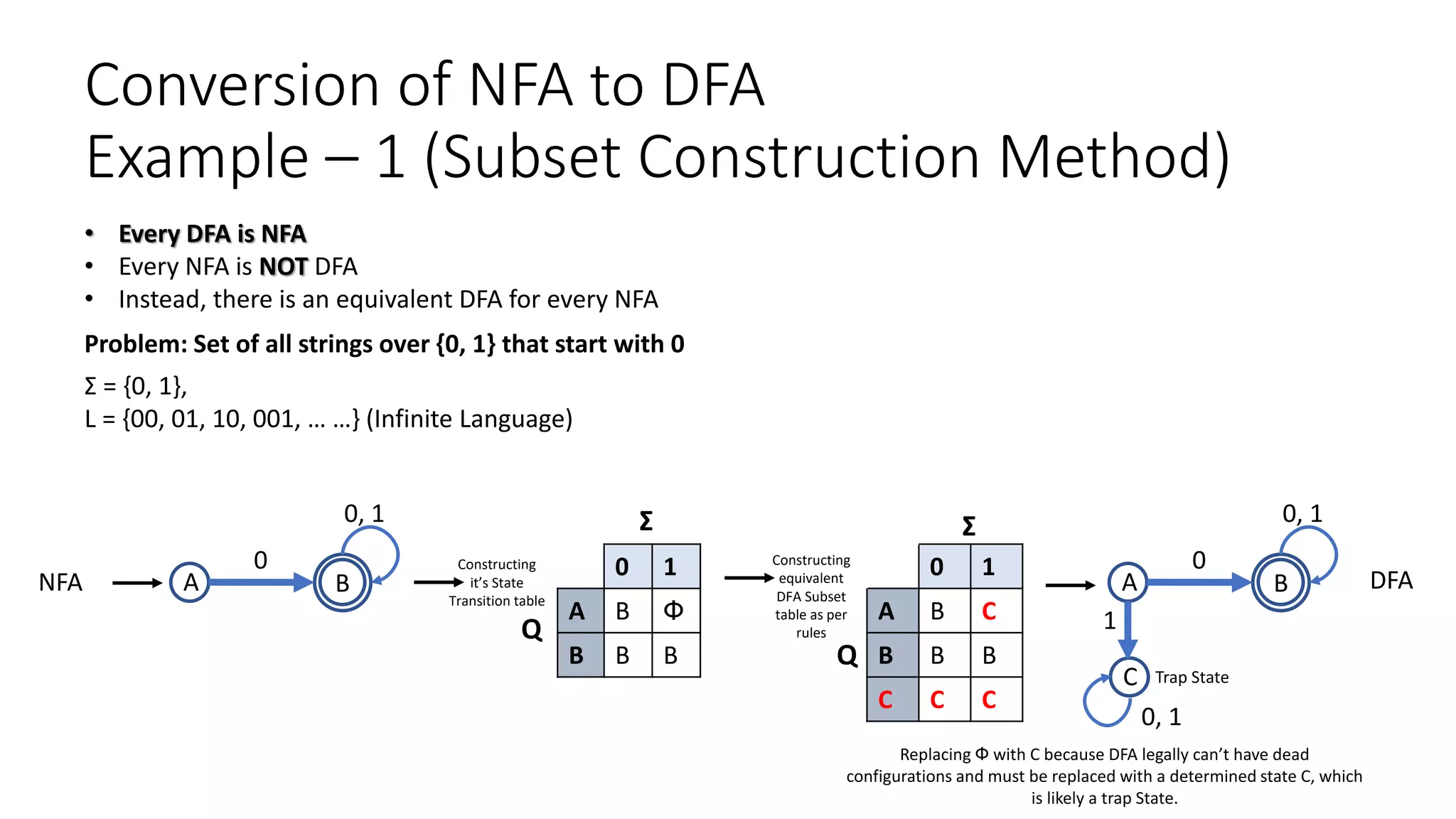
Here are the steps to solve the assignments: 1. Draw NFA and DFA over L = {0, 1} where machine should only accept at least two 1s NFA: A 1 B 0,1 1 C DFA: A 1 B 1 C 2. Draw DFA for following state transition table of NFA: A {A} {A, B} B {C} {C} C Փ Փ 0 1 DFA: A 0,1 B 1 C The key steps are to identify the states of the N

1. Computational Theory and
Automata

2. Rationale 1/2
• It is a study of abstract machines and the computation problems that
can be solved by using these machines.
• An Abstract Machine is a theoretical model that allows for a detailed
and precise analysis of how a computer system functions. The
abstract machine is referred to as “Automata”.
• The main motivation behind developing the automata theory was to
develop methods to describe and analyze the dynamic behavior of
discrete systems. (Example: Number Classification)
• Automata theory is a pure representation of computer science in
mathematics as a mathematical function that receives input, does
some processing and produces output.

3. Rationale 2/2
• Focuses on automation of tasks using computers/machines
• e.g.:
• Accept any binary string → 1110101
1011
0011111 etc…
• Accept any binary string that ends with “0” → 10010100
10001110
00111110 etc…
• Accept valid C++ code → Convert code to binary instructions (Compiler)

4. Computational Theory
Core
Finite State
Machine
Context Free Language
Turing Machine
Undecidable
Undecidable: The problems
that cannot be solved mechanically.
Tier 1
Tier 2
Tier 3
Tier 4

5. Tier 1
Finite State Machine

6. FSM - Prerequisites (1/3)
• Symbol: can be individual letters/numbers/characters
• a,b,c,1,2,3,A,B,C etc.
• Alphabet: Represented by ‘∑’ → Collection of Symbols
• ∑ = {a, b, c}
• ∑ = {1, 2, 3, 4}
• ∑ = {A, B}
etc.
• Strings: Sequence of Symbols
• a,b,c,aa,ab,bb,cc,01,0 etc.

7. FSM - Prerequisites (2/3)
• Language: Set of strings derived from alphabets
Example: For given alphabet ∑ = {a,b}, we can devise multiple languages as
below:
L1: Set of all strings are of length 2.
L1 = {aa, ab, ba, bb}
L2: Set of all strings are of length 3.
L2 = {aaa, aab, aba, abb, baa, bab, bba, bbb}
L3: Set of all strings begin with a.
L3 = {aaa, aab, aba, abb, aaaab, abbb, ... … (can have infinite strings because no length
given – hence infinite language) … …}

8. FSM - Prerequisites (3/3)
• Powers of ‘∑’:
For give alphabet ∑ = {a, b}
• ∑0 = set of all strings of length 0: {є} where ‘є’ represents epsilon
• ∑1 = set of all strings of length 1: {a, b}
• ∑2 = set of all strings of length 2: {aa, ab, ba, bb}
• ∑3 = set of all strings of length 3: {aaa, aab, aba, abb, baa, bab, bba, bbb}
• ∑n = set of all strings of length n
.
.
• ∑* = ∑0 U ∑1 U ∑2 … … …
∑* = {є}U {a, b} U {aa, ab, ba, bb} U {aaa, aab, aba, abb, baa, bab, bba, bbb} … … …
• Infinite Set of all possible strings of all lengths over {a, b} as given above.
.
.
• ∑+ = Infinite set of all possible strings of all possible lengths excluding ‘Ɛ’.
∑+ = ∑* - {є} → ∑+ = ∑1 U ∑2 U ∑3 … … … (also called as Positive Closure/Kleene Closure)
• Cardinality:
Total number of elements in a set → (cardinality)∑n = 2n

9. FSM – Finite Automata
Finite Automata
Finite Automata with output
Finite Automata without output
Moore
Machine
Mealy
Machine
Deterministic
Finite
Automata (DFA)
Non-deterministic
Finite
Automata (NFA)
є - Nondeterministic
Finite
Automata (є-NFA)
• It is the simplest machine to recognize patterns
• Simplest model of computation
• It has very limited memory
• The finite automata or finite state machine is an abstract
machine that has

10. Deterministic Finite Automata (DFA)
Has five elements or tuples:
Q : Finite set of states.
Σ : set of Input Symbols.
q : Initial state.
F : set of Final States.
δ : Transition Function from Q x Σ → Q.
A B
C D
0 0 0 0
1
1
1
1
Figure: DFA Machine
Values from given figure:
Q : {A, B, C, D}.
Σ : {0, 1}.
q : {A}.
F : {D}.
δ : Transition Function is →
C B
D A
A D
B C
1
0
A
B
C
D
Input Σ
States
(Q)
Table shows where
each state transfers
control corresponding
to its input

11. Deterministic Finite Automata (DFA)
Example - 1
Given Language: L1 = Set of all strings that start with ‘0’
= {0, 00, 01, 000, 010, 011, 0000, … … … } (Infinite Language)
A
C
1
B
0
0, 1
0, 1
A successful machine on this language will
always have string starting with ‘0’
Dead State/Trap State
Example: If we run 001 on this machine
Initial State A
First 0 of input
string passed to
state B
0
B
Second 0 of
input string
Looped back to
state B
0
B
Lastly, 1 of
input string
Looped back to
state B
1
B
Input Completed: B is
ending state, hence
input string validates
DFA machine
Example: If we run 101 on this machine
Initial State A
1 of input
string passed to
state C
1
C
Next, 0 of input
string Looped
back to state C
0
C
Lastly, 1 of
input string
Looped back to
state C again
1
C
Input Completed: C is
NOT ending state,
hence input string
doesn’t comply with
rule of language and
our DFA machine as
well

12. Deterministic Finite Automata (DFA)
Example - 2
Problem: Construct a DFA that accepts sets of all string over {0, 1} of length 2
First, we need to construct language out of it:
Σ = {0, 1}, L = {00, 01, 10, 11}
A
A successful machine on this language will
always have string length of 2
Dead
State/Trap
State
Example: If we run 00 on this machine
Initial State A
First 0 of input
string passed to
state B
0
B
Second 0 of
input string
passed to state
C
0
C
Input Completed: C is
ending state, hence
input string validates
DFA machine
Example: If we run 001 on this machine
Initial State A
0 of input
string passed to
state B
0
B
Next, 0 of input
string Looped
back to state C
0
C
Length of input
string exceeds
given language
(i.e 2), third
and final input
value “1” of
string is passed
to D
1
D
Input Completed: D is
NOT ending state,
hence input string
doesn’t comply with
rule of language and
our DFA machine as
well
B C D
Start 0,1 0,1 0,1
0,1
The reason to make another
state (D), is that we need to flush
out any input string that has
length of more than 2 length
If input string is less than 2, it
will not pass B and will not
proceed further, willingly
staying away from final state

14. NFA v/s DFA - Rationale
DETERMINISM
• In DFA, given the current state,
we know what the next state is.
• It has only one unique next
state.
• It has no choices or
randomness.
A B
C D
0 0 0 0
1
1
1
1
NON-DETERMINISM
• In NFA, given the current state,
there could be multiple next
states.
• The next state may be chosen at
random.
• All the next states maybe
chosen in parallel.
A
B
C
D
E
0
1
0
1
є

15. Nondeterministic Finite Automata (NFA)
Has five elements or tuples:
Q : Finite set of states.
Σ : set of Input Symbols.
q : Initial state.
F : set of Final States.
δ : Transition Function
Figure: NFA Machine
Values from given figure:
Q : {A, B,}.
Σ : {0, 1}.
q : {A}.
F : {B}.
δ : Transition Function is → Q x Σ = ?
A B
0
0, 1
L = {set of all strings the end with 0}
Generated Inputs
A given 0 →
A given 0 →
A given 1 →
B given 0 →
B given 1 →
A
B
A
Փ
Փ
Transitional States→ A, B, AB , Փ Transitioning
pattern on
the basis of
generated
inputs
Incase there are 3 input
States A, B, C:
Parallel transition as per
NFA rules discussed earlier
Possible Transitions: 4
A input→ A, B, C, AB, AC,
BC, ABC, Փ
Possible Transitions: 8
= 22
= 23
Transition Function δ is → Q x Σ = 2Q

16. Nondeterministic Finite Automata (NFA)
Example - 1
Given Language: L1 = Set of all strings that end with ‘0’
= {0, 00, 010, 000, 110, 0000, … … … } (Infinite Language)
A successful machine on this language will
always have string ending with ‘0’
AND
If there is any way to run the machine that
ends in any set of states out of which
at least one state is a final state,
then NFA accepts the process
A B
0
0, 1
From previous example
Example: If we run 100 on this machine
Initial State A
1
A
0
A
0
B Փ
A
B
A is not a concluding state,
so it will not be an
appropriate path
B is an ending state, so it is
an appropriate path of this
NFA machine
Example: If we run 01 on this machine
Initial State A
0
1
Փ
A
A is not a concluding state,
so it will not be an
appropriate path
A
B

17. Nondeterministic Finite Automata (NFA)
Example - 2
Given Language: L1 = Set of all strings that start with ‘0’
= {0, 00, 000, 0001, 0110, 0000, … … … } (Infinite Language)
A successful machine on this language will
always have string starting with ‘0’
AND
If there is any way to run the machine that
ends in any set of states out of which
at least one state is a final state,
then NFA accepts the process
A B
0
0, 1
Example: If we run 001 on this machine
Initial State A
0
B
0 B is an ending state, so the
string is accepted
Example: If we run 101 on this machine
Initial State A
1
Փ
B
1
B
Goes nowhere. A state that
does not lead to anywhere is
called as “Dead
Configuration”
“DFA is not allowed to have dead
configuration because of its Deterministic
model, and it has to drain all states into
transition.
NFA, because of its Non-Deterministic
model, can have dead configuration with
appropriate paths”

18. DFA vs NFA – Class Exercise
Problem: For {a, b} Design FSM, that accepts at least one ‘a’ and must end with exactly one ‘b’
DFA
A
a
a
B
B
a
b
b
b
NFA
A
a
B
B
b
a , b

19. Conversion of NFA to DFA
Example – 1 (Subset Construction Method)
• Every DFA is NFA
• Every NFA is NOT DFA
• Instead, there is an equivalent DFA for every NFA
Problem: Set of all strings over {0, 1} that start with 0
Σ = {0, 1},
L = {00, 01, 10, 001, … …} (Infinite Language)
NFA A B
0
0, 1
Constructing
it’s State
Transition table
0 1
A B Փ
B B B
Σ
Q
Constructing
equivalent
DFA Subset
table as per
rules
0 1
A B C
B B B
C C C
Σ
Q
Replacing Փ with C because DFA legally can’t have dead
configurations and must be replaced with a determined state C, which
is likely a trap State.
A B
0
0, 1
C
1
Trap State
DFA
0, 1

20. Conversion of NFA to DFA
Example - 2 (Subset Construction Method)
NFA A B
1
0, 1
Constructing
it’s state
transition table
0 1
A A A,B
B Փ Փ
Σ
Q
Constructing
equivalent
DFA subset
table as per
rules
Problem: Set of all strings over {0, 1} that ends with 1
Σ = {0, 1},
L = {001, 01, 101, 001, … …} (Infinite Language)
0 1
A A AB
AB A AB
Σ
Q
• Union of A and B over “0” input value, which is “A”, as B in NFA State
Transition table is null, and A is “A”
• Union of A and B over “1” input value, which is “AB” (union), as B in
NFA State Transition table is null, and A is “A, B”
1
A AB
1
0
DFA
0
A is leading towards two states simultaneously
A,B in State transition Table of NFA. In DFA, a
state is prohibited to transfer same value to
more than one state simultaneously. the value
will be replaced with a new state created by
union of A and B

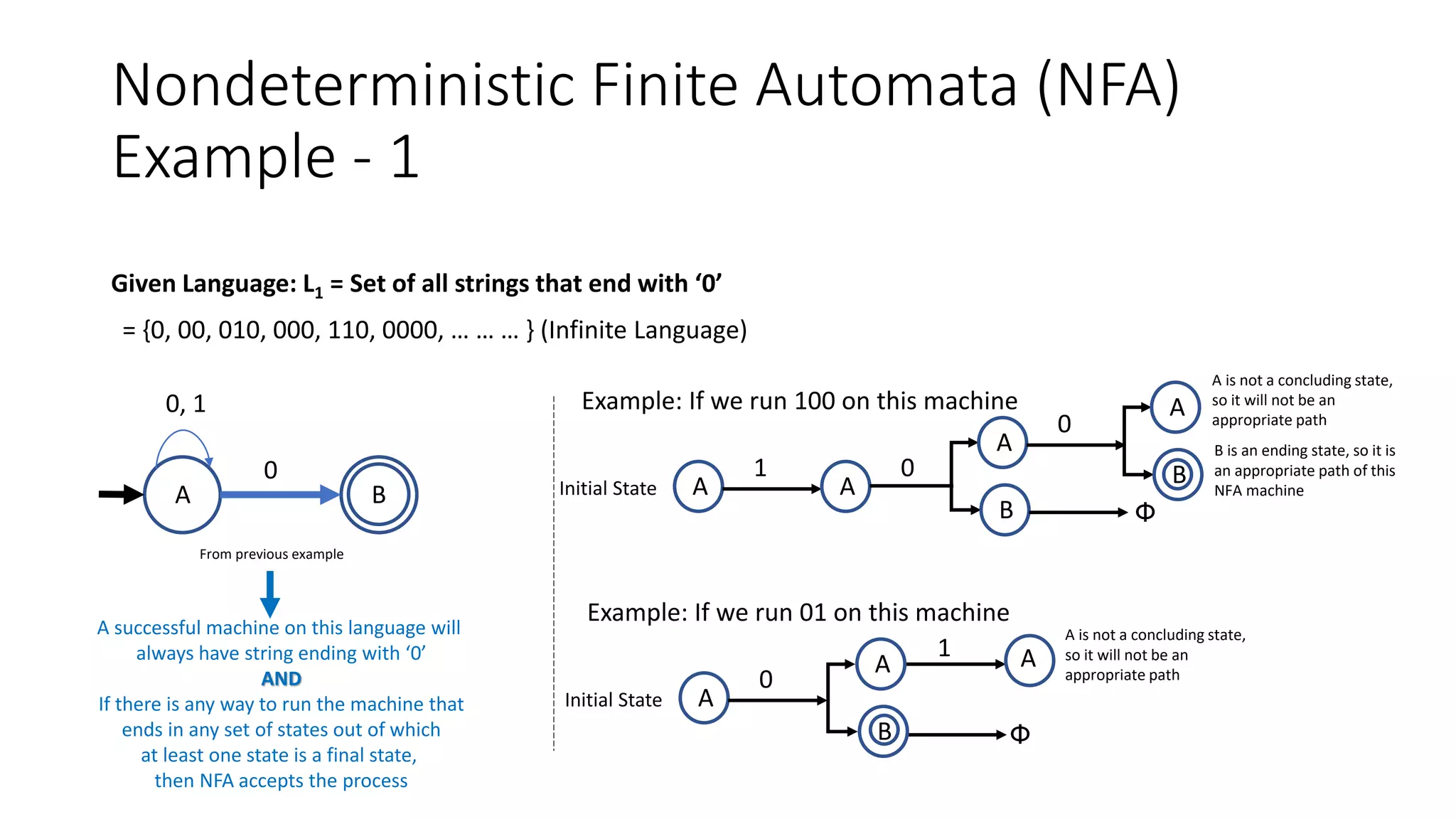
21. Conversion of NFA to DFA
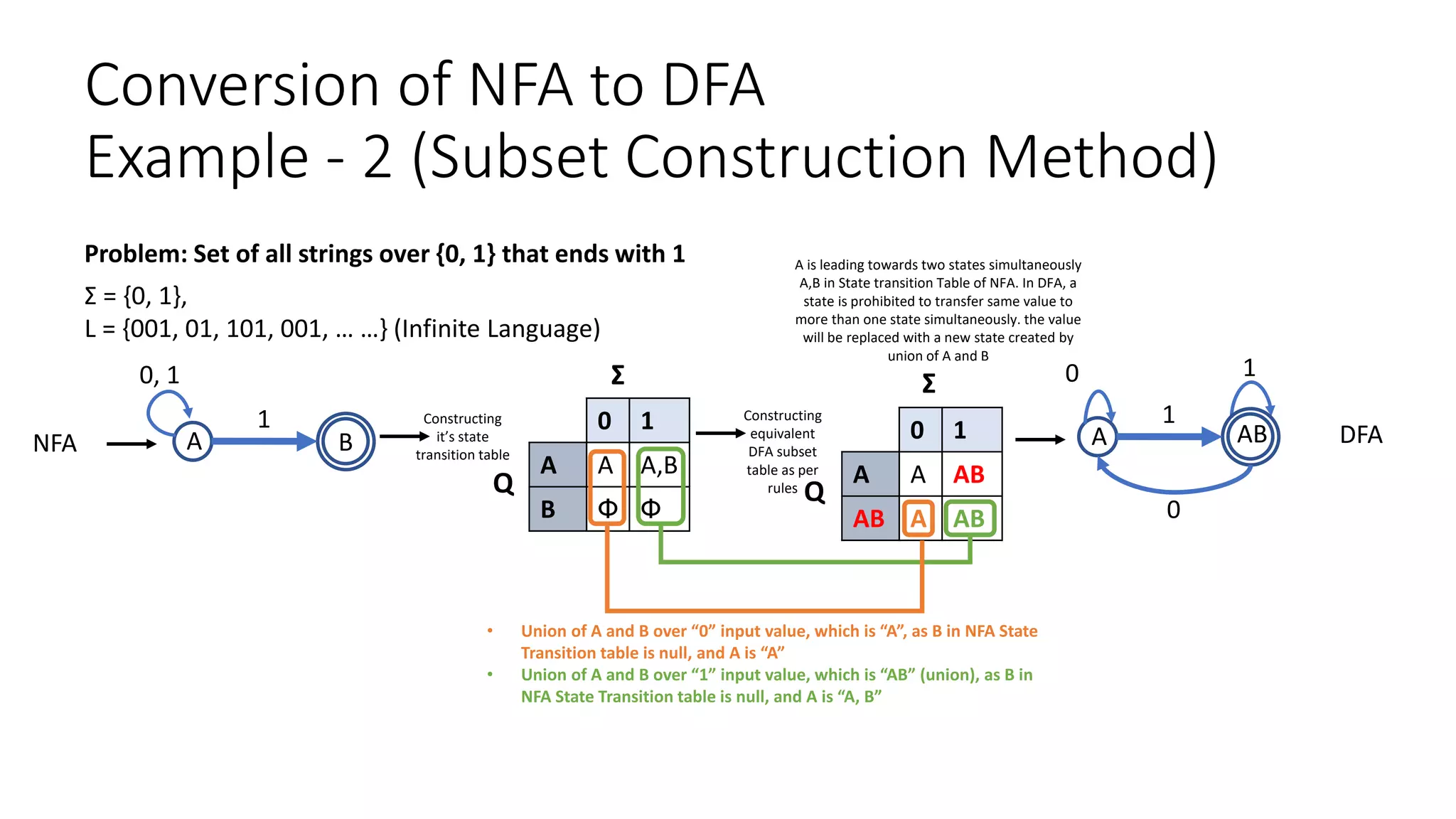
Example – 3 (Subset Construction Method)
a b
A AB C
AB AB BC
BC A AB
C D AB
D D D
Find the equivalent DFA for the NFA given by M = [{A,B,C}, (a,b), δ, A, {C} ] where δ is
given by:
a b
A A,B C
B A B
C - A,B
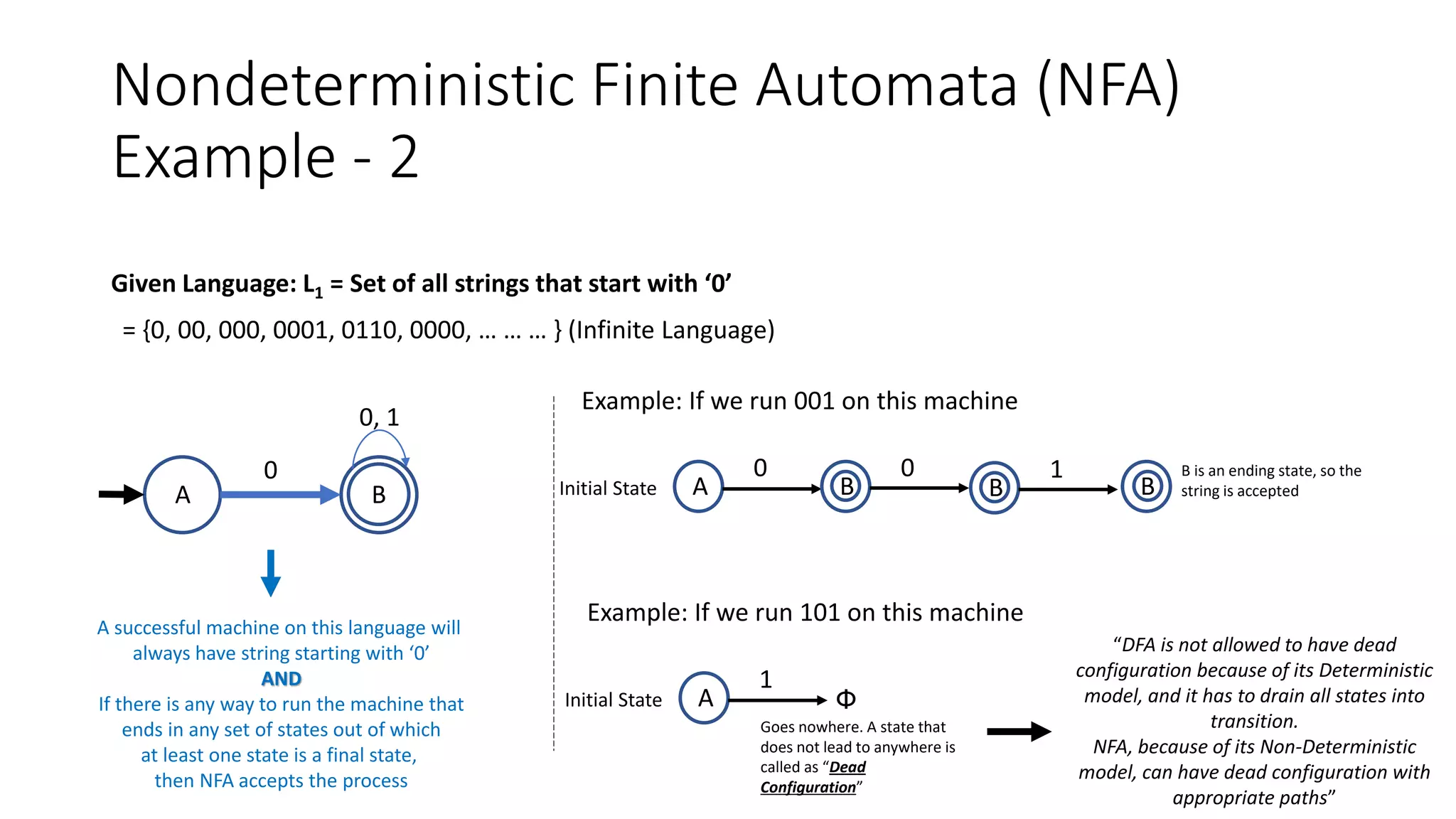
Σ
Q
=
M = [{A,B,C}, (a, b), δ, A, {C} ]
Q Σ δ q F
Formal Representation
of an NFA
A B
a b
C
b
NFA State
Transition
Diagram
a
b a
b
Union of A, B from given δ against
corresponding 0 and 1
Union of B, C from given δ against
corresponding 0 and 1
Combining 2 states into one in order to maintain
deterministic property
“C” was final state in given δ, so
we will make every state final
which have C
AB
A
D
C
BC
a
b b
a
a
b
b
a
a,b Remember! It is most likely
that you’ll find next state
while constructing
transition table for DFA. You
have to use given NFA table
for union operations only
“
“

22. Assignments
1 - Draw NFA and DFA over L = {0, 1} where machine should only accept at least two 1s
2 - Draw DFA for following state transition table of NFA:
A {A} {A, B}
B {C} {C}
C Փ Փ
0 1