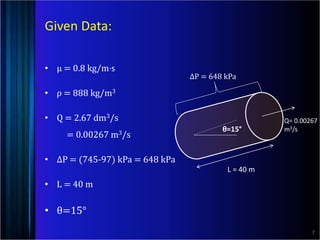
This document presents the analysis of steady, laminar flow of oil through an inclined pipe. The given information includes the properties of the oil, flow rate, inlet and outlet pressures, pipe length and inclination. An equation for force balance in inclined pipes is derived. Using this, the Hagen-Poiseuille equation is modified to calculate the pipe diameter. The calculations determine the pipe diameter to be 5.0 cm. The Reynolds number is also calculated and found to be less than 2100, confirming the flow is laminar as assumed. Therefore, the analysis is valid.

1. Fluid Flow Numerical
Chandrima Shrivastava
13FET1001
1

2. Numerical
• Oil at 20°C (ρ = 888 kg/m3 and µ = 0.800 kg/m·s) is
flowing steadily through a 40-m-long pipe with a flow
rate of 2.67 dm3/s. The pipe is inclined 15° upward.
• The pressure at the pipe inlet and outlet are
measured to be 745 and 97 kPa, respectively.
Determine the flow diameter of the pipe. Also verify
that the flow through the pipe is laminar.
2

3. Assumptions
• The flow is steady and incompressible
• The entrance effects are negligible, and thus the flow is fully
developed
• The entrance and exit loses are negligible
• The flow is laminar (to be verified)
• The pipe involves no components such as bends, valves, and
connectors
• The piping section involves no work devices such as pumps and
turbine
• Neglecting frictional losses in the pipe
3

4. Inclined Pipes – Force Balance
P
4

5. 

sin
)(
gr
dx
dPr
dr
rd



r
L
P
r
L
gLP
rg
L
P
dr
rd





 





 









 'sin
sin
)( 


1
2
2
'
c
r
L
P
r 




 
 01 c











 

dr
dv
r
L
P

2
'











 








 2
2
2
2
22
1
4
sin
1
4
'
R
r
R
L
gLP
R
r
L
RP
v



Integrating & putting v=0 at r=R (NO SLIP),
L
RP
c
4
' 2
2


Derivation of Velocity Profile
Velocity
profile
5

6. 










 








 2
2
2
2
22
1
4
sin
1
4
'
R
r
R
L
gLP
R
r
L
RP
v



Analogous to fluid flow through a horizontal pipe,
Average velocity
2
32
sin
D
L
gLP
vavg 




 



Velocity profile
6
Volumetric flow rate (Q)
42
128
sin
4
D
L
gLP
DvQ avg 







 


7. Given Data:
• µ = 0.8 kg/m·s
• ρ = 888 kg/m3
• Q = 2.67 dm3/s
= 0.00267 m3/s
• ∆P = (745-97) kPa = 648 kPa
• L = 40 m
• θ=15°
L = 40 m
Q= 0.00267
m3/s
∆P = 648 kPa
θ=15°
7

8. Applying modified Hagen-Poiseuille equation
44
838.427
128
sin
DD
L
gLP
Q 




 
 


43
838.4271067.2 DQ  
mD 05.0
sm
D
A
Q
vavg /36.1
4
1067.2
2
3





75
8.0
88836.105.0
Re 



avgDv
Which is < 2100
Therefore the flow is laminar and the analysis is valid.
8

9. 9