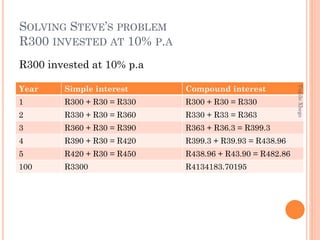
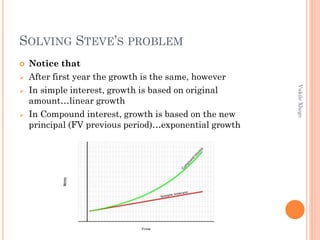
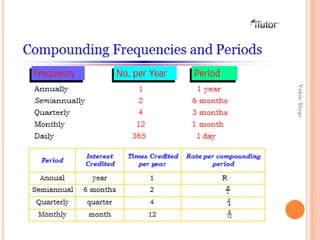
The document discusses simple and compound interest. It defines both types of interest and provides formulas to calculate future value under each. An example is shown where a learner named Steve invests R300 at 10% interest annually under simple and compound interest over 3 years. Compound interest provides a higher return due to interest earning interest each period. The document encourages choosing investments that use compound versus simple interest.

1. FINANCIAL MATHEMATICS
Simple and Compound interest

2. SPECIFIC AIMS



Vukile Xhego

By the end of the lesson, learners should be able
to:
Define compounded and simple interest
Apply compound and simple interest formulae to
calculate future value of an investment/loan
Appreciate the knowledge of compound and
simple interest in real life situations, e.g:
choosing a better investment/loan offer

3. SPECIFIC AIMS

After the lesson learners will be able to differentiate

They will be able to calculate interest earned

Learners will be able to calculate any variable when
given adequate information

The can find interest; number of years ;future value;
principal amount, etc.

Differentiate between different types of interest rate,
example compounded monthly , semi-annual,
annually, quarterly and so on
Vukile Xhego
between simple interest and compound interest

4. INTRODUCTION

When you borrow money from someone
Vukile Xhego

5. INTRODUCTION

You have to pay back service charge to the lender
Vukile Xhego
This money is paid back to the lender along with
the amount borrowed
 Sometimes called the Cost of Money or Interest


6. SIMPLE INTEREST
Interest earned only on original amount
 Linear/straight-line increase
Formula
 An investment of PV rands growing with simple
interest rate i after n years is worth FV rands:


where;

FV is the future value



PV is the present/principal value
i is the interest rate
n is time in years
Vukile Xhego
FV = PV + PV*in = PV(1 + in)

7. EXAMPLE

Vukile Xhego
Steve invested R 300 on an account which pays
10% simple interest. How much will his
investment be worth after 3 years?

8. EXAMPLE 1: SOLUTION
Organise information:
 PV = R300, i = 10% = 0.1, n = 3yrs, FV =?

Vukile Xhego
We know that:
 FV = PV(1 + in) = 300(1 + (0.1)3) = 390
 Therefore his investment will be worth R390.00
after 3 years


9. COMPOUND INTEREST

Vukile Xhego
Another bank approaches Steve and claims they
will give him a better offer that will earn him
interest at the same interest rate, but
compounded yearly

10. COMPOUND INTEREST
How much will his invest be worth after the 3
years?
 Which investment would you advise Steve to opt
for? Why?

Vukile Xhego

11. COMPOUND INTEREST
This is interest calculated not only on the original
investment but as well as on the interest that has
been earned previously
 Exponential growth
 An investment of PV rands earning interest at
an annual rate i compounded m times a year for
a period of n years is worth FV rands:

Vukile Xhego
FV = PV(1+i/m)n*m

12. COMPOUND INTEREST
Where;
 FV is the future value
 PV is the principal/present value
 i is interest rate
 n is the period of investment/loan
 m is the number of compounding periods in one
year

Vukile Xhego

13. SOLVING STEVE’S PROBLEM
Organise info:
 PV = 300, i = 10%, n = 3yrs, m = 1, FV = ?
 FV = PV(1+i/m)^n*m


b) Thus this would be the best option. To answer
the why question, let’s look at a table…
Vukile Xhego
Substitute:
 FV = 300(1 + 0.1/1)^3(1)

= 399.3


14. SOLVING STEVE’S PROBLEM
R300 INVESTED AT 10% P.A
R300 invested at 10% p.a
Simple interest
Compound interest
1
R300 + R30 = R330
R300 + R30 = R330
2
R330 + R30 = R360
R330 + R33 = R363
3
R360 + R30 = R390
R363 + R36.3 = R399.3
4
R390 + R30 = R420
R399.3 + R39.93 = R438.96
5
R420 + R30 = R450
R438.96 + R43.90 = R482.86
100
R3300
R4134183.70195
Vukile Xhego
Year

15. SOLVING STEVE’S PROBLEM



Vukile Xhego

Notice that
After first year the growth is the same, however
In simple interest, growth is based on original
amount…linear growth
In Compound interest, growth is based on the new
principal (FV previous period)…exponential growth

16. SOLVING STEVE’S PROBLEM

Vukile Xhego
Thus exponential investment will yield much
better returns than linear investment…a good
option for Steve

17. SOLVING STEVE’S PROBLEM

A good option for YOU too…
Vukile Xhego

18. Vukile Xhego

19. REFERENCES
Iniego D. (2014): http://www.slideshare.net/IniegoDianne/compoundinterest-29921929?qid=b1cbfc82-2060-4cc5-aad0b82ce0100578&v=default&b=&from_search=1

Bruce C. (2010) : http://www.slideshare.net/brucecoulter/lesson-4compound-interest-2009

Mike Glenon (2012): http://www.slideshare.net/glennontech/simpleinterest-vs-compound-interest?qid=03f1d1bf-4878-41ac-84d882f9c9b3ace9&v=qf1&b=&from_search=1#btnNext

Mahapatra H.S. (2013) : http://www.slideshare.net/hisema/simpleand-compound-interest-24834757?qid=03f1d1bf-4878-41ac-84d882f9c9b3ace9&v=qf1&b=&from_search=3

Vukile Xhego
Itutor. (2013) : http://www.slideshare.net/itutor/compound-interest26220842


20. REFERENCE

Vukile Xhego

Images taken from:
Google Images: http//:google.co.za/images