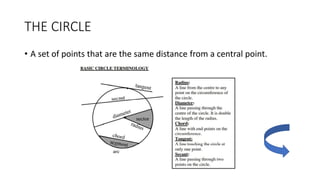
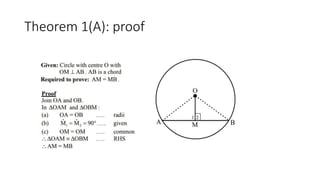
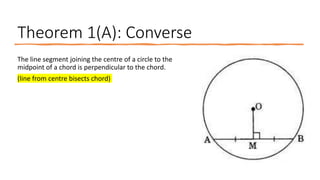
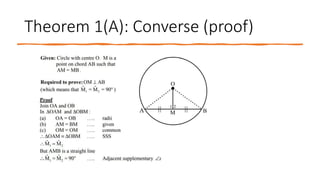
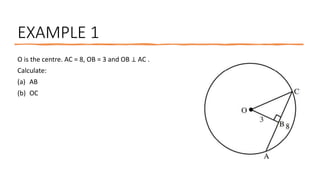
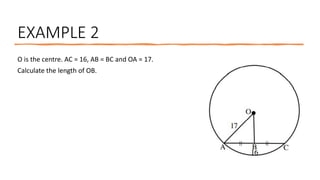
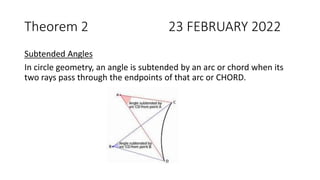
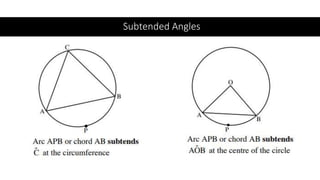
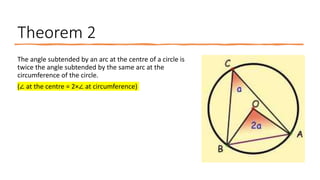
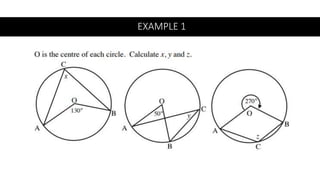
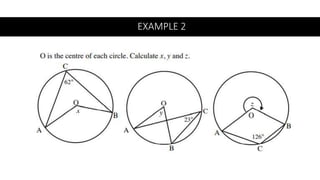
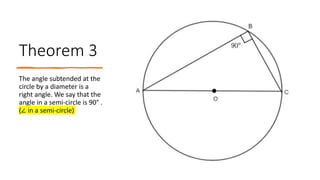
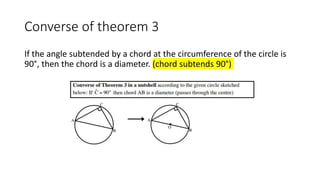
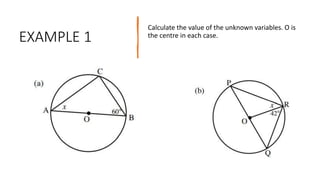
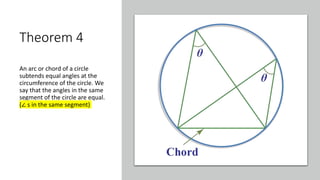
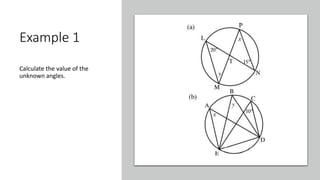
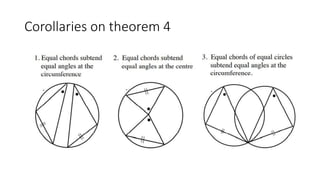
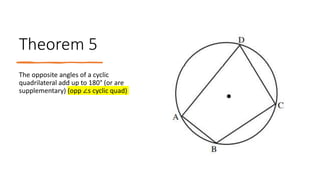
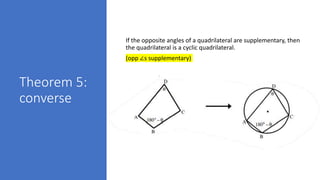
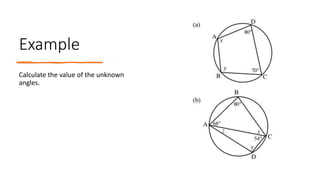
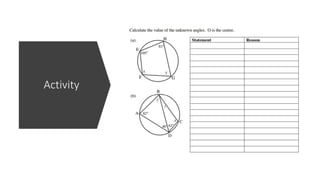
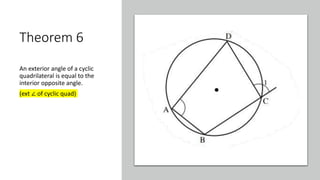
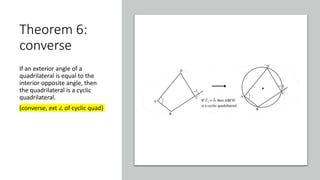
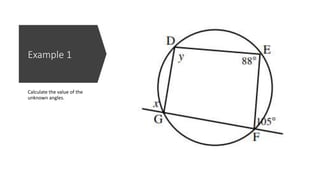
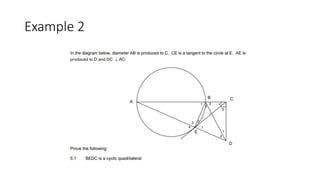
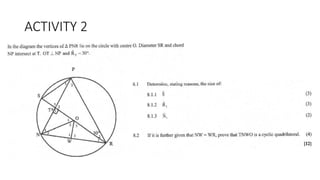
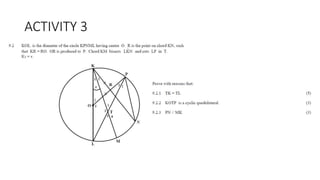
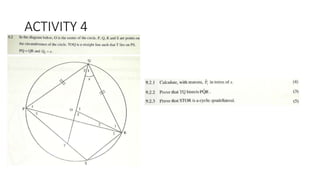
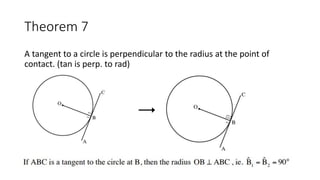
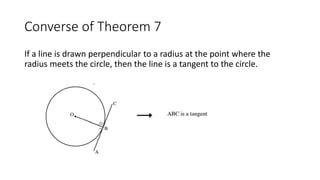
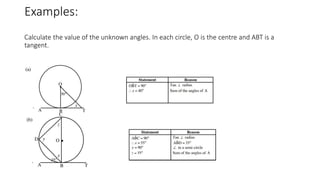
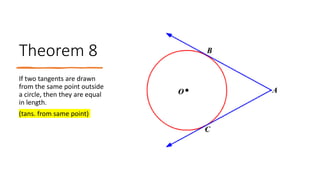
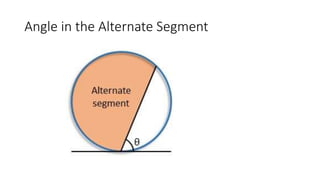
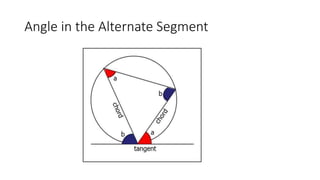
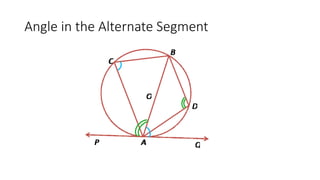
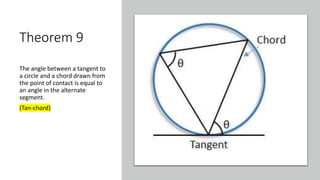
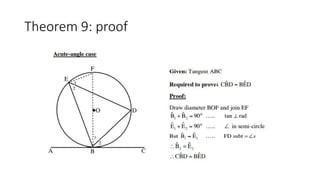
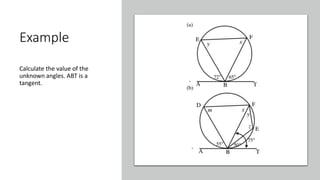
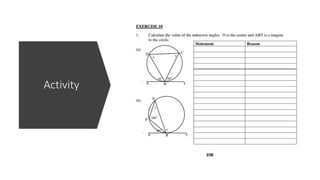
The document provides a comprehensive overview of circle geometry for grade 11, covering key concepts, theorems, and proofs related to circles, angles, and cyclic quadrilaterals. It outlines the importance of geometry in developing critical thinking and problem-solving skills and includes numerous examples and activities for students. Specific theorems discussed include those related to perpendiculars, subtended angles, cyclic quadrilaterals, and properties of tangents.

1. EUCLIDEAN GEOMETRY
CIRCLE GEO (GR.11)

2. INTRODUCTION (HISTORY)

3. INTRODUCTION
The study of geometry contributes to helping students develop the
skills of:
• Visualisation,
• Critical thinking,
• Intuition,
• Perspective,
• Problem-solving,
• Conjecturing, deductive reasoning, logical argument and proof.

4. THE CIRCLE
• A set of points that are the same distance from a central point.

5. Theorem 1(A)
The perpendicular drawn from the centre of a circle to a
chord bisects the chord. (perp. from centre to cord)

6. Theorem 1(A): proof

7. Theorem 1(A): Converse
The line segment joining the centre of a circle to the
midpoint of a chord is perpendicular to the chord.
(line from centre bisects chord)

8. Theorem 1(A): Converse (proof)

9. EXAMPLE 1
O is the centre. AC = 8, OB = 3 and OB ⊥ AC .
Calculate:
(a) AB
(b) OC

10. EXAMPLE 2
O is the centre. AC = 16, AB = BC and OA = 17.
Calculate the length of OB.

11. Activity

12. Theorem 2 23 FEBRUARY 2022
Subtended Angles
In circle geometry, an angle is subtended by an arc or chord when its
two rays pass through the endpoints of that arc or CHORD.

13. Subtended Angles

14. Theorem 2
The angle subtended by an arc at the centre of a circle is
twice the angle subtended by the same arc at the
circumference of the circle.
(∠ at the centre = 2×∠ at circumference)

15. Theorem 2:
proof

16. EXAMPLE 1

17. EXAMPLE 2

18. Theorem 3
The angle subtended at the
circle by a diameter is a
right angle. We say that the
angle in a semi-circle is 90° .
(∠ in a semi-circle)

19. Converse of theorem 3
If the angle subtended by a chord at the circumference of the circle is
90°, then the chord is a diameter. (chord subtends 90°)

20. EXAMPLE 1
Calculate the value of the unknown variables. O is
the centre in each case.

21. Activity
Exercise 2 (p.217-219)
a, b, c, d, e, i, and j.
Exercise 3 (p.221)
a, b, c, and d.

22. Cyclic Quadrilaterals
24 FEBRUARY 2022

23. Theorem 4
An arc or chord of a circle
subtends equal angles at the
circumference of the circle. We
say that the angles in the same
segment of the circle are equal.
(∠ s in the same segment)

24. Theorem 4:
Proof

25. Theorem 4:
Converse
If a line segment joining two points subtends equal angles
at two other points on the same side of the line segment,
then these four points are concyclic (converse of angles in
same segment)

26. Example 1
Calculate the value of the
unknown angles.

27. Activity

28. Corollaries on theorem 4

30. Theorem 5
The opposite angles of a cyclic
quadrilateral add up to 180° (or are
supplementary) (opp ∠s cyclic quad)

31. Theorem 5:
Proof

32. Theorem 5:
converse
If the opposite angles of a quadrilateral are supplementary, then
the quadrilateral is a cyclic quadrilateral.
(opp ∠s supplementary)

33. Example
Calculate the value of the unknown
angles.

34. Activity

35. Theorem 6
An exterior angle of a cyclic
quadrilateral is equal to the
interior opposite angle.
(ext ∠ of cyclic quad)

36. Theorem 6:
converse
If an exterior angle of a
quadrilateral is equal to the
interior opposite angle, then
the quadrilateral is a cyclic
quadrilateral.
(converse, ext ∠ of cyclic quad)

37. Summary: How to prove that a quadrilateral is cyclic

38. Example 1
Calculate the value of the
unknown angles.

39. Example 2

40. Activity

41. Revision and Consolidation

42. Revision and Consolidation

43. Revision and Consolidation

44. ACTIVITY 1

45. ACTIVITY 2

46. ACTIVITY 3

47. ACTIVITY 4

48. ACTIVITY 5

49. Tangents to
Circles

50. Recall
A tangent…

51. Theorem 7
A tangent to a circle is perpendicular to the radius at the point of
contact. (tan is perp. to rad)

52. Converse of Theorem 7
If a line is drawn perpendicular to a radius at the point where the
radius meets the circle, then the line is a tangent to the circle.

53. Examples:
Calculate the value of the unknown angles. In each circle, O is the centre and ABT is a
tangent.

54. Activity: Exe 8

55. Theorem 8
If two tangents are drawn
from the same point outside
a circle, then they are equal
in length.
(tans. from same point)

56. Activity:

57. Angle in the Alternate Segment

58. Angle in the Alternate Segment

59. Angle in the Alternate Segment

60. Theorem 9
The angle between a tangent to
a circle and a chord drawn from
the point of contact is equal to
an angle in the alternate
segment.
(Tan-chord)

61. Theorem 9: proof

62. Converse of
theorem 9
If a line is drawn through the endpoint of a chord, making
with the chord an angle equal to an angle in the alternate
segment, then the line is a tangent to the circle.
(converse, tan-chord)

63. Example
Calculate the value of the
unknown angles. ABT is a
tangent.

64. Activity