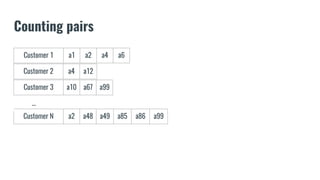
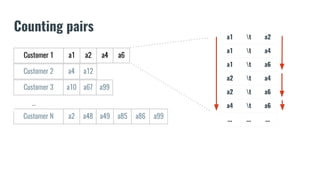
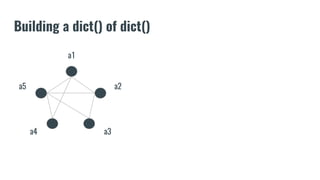
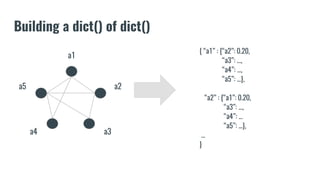
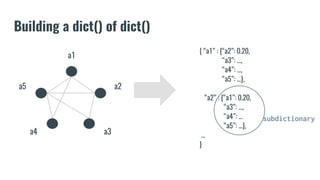
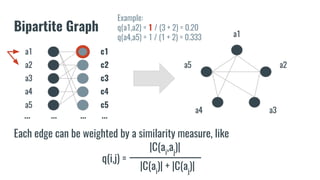
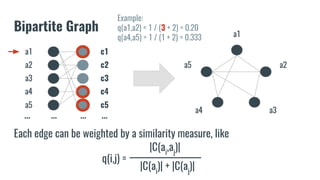
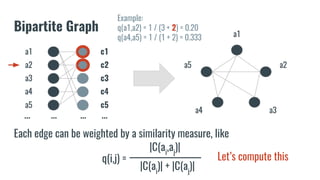
The document discusses recommendation systems in banking and financial services. It describes different types of recommendation systems including content-based filtering, collaborative filtering, and hybrid filtering. It then discusses how recommendation systems could be useful in banking by using a bipartite graph and word embedding approaches to represent customer and asset data and identify relationships between them. Code examples are provided for implementing some of these recommendation system techniques.

1. Let the music play!
Recommendation Systems in
Banking & Financial Services
Pycon8
Florence
April 7th, 14.30
Andrea Gigli @andrgig
andrgig@gmail.com

2. Who I am
Andrea Gigli #DataGeek, #BusinessDeveloper, #DataLover,
find me on twitter @andrgig
By day: Trading Desk Manager, Quantitative Analyst,
Data-driven Project Manager in the Banking Sector.
By night: Data Scientist, Lecturer in Data Science for
Management, Startup Mentor, Event Organizer (did you
enjoy DataBeers yesterday?)
MSc in Big Data Analytics and Social Mining (2016), PhD
in Statistics (2003), MSc in Quantitative Finance (2000)

3. Florence, April 6th 2017
powered by

4. Who I am
Andrea Gigli #DataGeek, #BusinessDeveloper, #DataLover,
find me on twitter @andrgig
By day: Trading Desk Manager, Quantitative Analyst,
Data-driven Project Manager in the Banking Sector.
By night: Data Scientist, Lecturer in Data Science for
Management, Startup Mentor, Event Organizer (did you
enjoy DataBeers yesterday?)
MSc in Big Data Analytics and Social Mining (2016), PhD
in Statistics (2003), MSc in Quantitative Finance (2000)

5. “All models are wrong,
but some are useful.”
George E. P. Box, 1976

6. Why Recommendation Systems are useful
Alternative to Search Engines
Useful in the era of Information Deluge and Digital Laziness
Very successful stories around (my favourites are Spotify, Pandora, Last.fm)

7. Type of Recomendation Systems
Content-based Filtering
Collaborative Filtering
Hybrid Filtering

8. Type of Recomendation Systems
Content-based Filtering
Collaborative Filtering
Hybrid Filtering

9. Content-based Filtering
Requires an understanding of the item
The understanding is expressed as a set of features
Usually the weight of each feature, for each user, is adjusted accordingly to
explicit user feedbacks
… limited scope start problem

10. Collaborative Filtering
Doesn’t require an understanding of the item itself
Requires large amount of data
Assumes that people who agreed in the past will agree in the future

11. Hybrid System
Combines multiple techniques together to achieve some synergy between
them
Solve the “cold start” problem in Collaborative Filtering
Solve the “limited scope” problem in Content-based Filtering

12. Are Recommendation Systems useful in banking?
Tons of papers have been written on quantitative models for “Portfolio
Selection” problems
● built on features which are asset-specific (for example risk and return)
● based on hypotheses which are not always true (for example investors
are risk-adverse)

13. “Beware of geeks
bearing formulas.”
W. Buffet, 2009

14. “In God we trust,
all the others must bring Data.”
W. E. Deming

15. A Paradigm shift
Computer
Machine
Data
Program
Solution

16. A Paradigm shift
Computer
Machine
Data
Program
Solution
Computer
Machine
Program
Data
Solution

17. Euler, 1736

18. Euler, 1736

19. Let’s represent our input data as two sets of nodes, the first related to
assets and the second to customers
C = {c1, c2, c3, ...}
A = {a1, a2, a3, ….}
In our case |C|>>|A|
Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
............
Customer set
Asset set

20. Let’s represent our input data as two sets of nodes, the first related to
assets and the second to customers, and draw who bought what
C = {c1, c2, c3, ...}
A = {a1, a2, a3, ….}
In our case |C|>>|A|
Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
............
Customer set
Asset set

21. Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
a1
a2
a3a4
a5
............

22. Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
a1
a2
a3a4
a5
Each edge can be weighted by a similarity measure, like
|C(ai
)| + |C(aj
)|
|C(ai
,aj
)|
q(i,j) =
............

23. Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
a1
a2
a3a4
a5
Each edge can be weighted by a similarity measure, like
|C(ai
)| + |C(aj
)|
|C(ai
,aj
)|
q(i,j) =
Example:
q(a1,a2) = 1 / (3 + 2) = 0.20
q(a4,a5) = 1 / (1 + 2) = 0.333
............

24. Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
a1
a2
a3a4
a5
Each edge can be weighted by a similarity measure, like
|C(ai
)| + |C(aj
)|
|C(ai
,aj
)|
q(i,j) =
Example:
q(a1,a2) = 1 / (3 + 2) = 0.20
q(a4,a5) = 1 / (1 + 2) = 0.333
............

25. Bipartite Graph
a1
a2
a3
a4
a5
c1
c2
c3
c4
c5
a1
a2
a3a4
a5
Each edge can be weighted by a similarity measure, like
|C(ai
)| + |C(aj
)|
|C(ai
,aj
)|
q(i,j) =
Example:
q(a1,a2) = 1 / (3 + 2) = 0.20
q(a4,a5) = 1 / (1 + 2) = 0.333
............
Let’s compute this

26. Hands on code now

27. Counting assets
a1 t 200
a2 t 1850
a3 t 800
a4 t 1100
a5 t 120
... ... ...
asset_counts = {}
with open("asset_counts.txt", 'r') as f:
for line in f:
items = line.split(‘t’)
asset, count = items[0], items[1]
dict_asset_counts[asset] = count
Let’s assume we saved on the file “asset_counts.txt” the counts for each
available asset on our dataset and we want to save them in a dict()

28. Counting pairs
Customer 1 a1 a2 a4 a6
Customer 2 a4 a12
Customer 3 a10 a67 a99
Customer N a2 a48 a49 a85 a86 a99
...

29. Counting pairs
Customer 1 a1 a2 a4 a6
Customer 2 a4 a12
Customer 3 a10 a67 a99
Customer N a2 a48 a49 a85 a86 a99
...

30. Counting pairs
Customer 1 a1 a2 a4 a6
Customer 2 a4 a12
Customer 3 a10 a67 a99
Customer N a2 a48 a49 a85 a86 a99
...
a1 t a2
a1 t a4
a1 t a6
a2 t a4
a2 t a6
a4 t a6
... ... ...

31. Counting pairs
Customer 1 a1 a2 a4 a6
Customer 2 a4 a12
Customer 3 a10 a67 a99
Customer N a2 a48 a49 a85 a86 a99
...
a1 t a2
a1 t a4
a1 t a6
a2 t a4
a2 t a6
a4 t a6
... ... ...
Save on the file “asset_pairs.txt” an ordered version of the asset pairs
observed in all customers’ portfolios.

32. Computing similarities
|C(ai
)| + |C(aj
)|
|C(ai
,aj
)|
q(i,j) =
Remember that our goal is to compute
dict_asset_counts → contains |C(ai
)| and |C(aj
)|
dict_pair_counts → contains |C(ai
,aj
)| for each i, j where i != j

33. Building a dict() of dict()
a1
a2
a3a4
a5

34. Building a dict() of dict()
{ “a1” : {“a2”: 0.20,
“a3”: ...,
“a4”: ...,
“a5”: ...},
“a2” : {“a1”: 0.20,
“a3”: ...,
“a4”: ...
“a5”: ...},
…
}
a1
a2
a3a4
a5

35. Building a dict() of dict()
{ “a1” : {“a2”: 0.20,
“a3”: ...,
“a4”: ...,
“a5”: ...},
“a2” : {“a1”: 0.20,
“a3”: ...,
“a4”: ...
“a5”: ...},
…
}
a1
a2
a3a4
a5
subdictionary

36. “Markets are
conversations.”
The Cluetrain Manifesto, 1999

37. Word Embedding
Methodology for mapping words or phrases from vocabulary to vectors of
real numbers.
0.123 ... 5.344 -0.253
...
2.333 ... 1.296 0.345
-0.453 ... 0.111 9.543
markets
are
conversations
...

38. Word2Vec
Word2vec model takes as its input a large corpus of text and produces a
vector space, with each unique word in the corpus being assigned a
corresponding vector in the space.
Word vectors are positioned in the vector space such that words that
share common contexts in the corpus are located in close
proximity to one another in the space.

39. Why context is relevant
Word vectors capture linguistic regularities
vec(“Paris”) - vec(“France”) + vec(“Italy”) is close to vec(“Rome”)
vec(“walking”) - vec(“swimming”) + vec(“swam”) is close to vec(“walked”)

40. “You shall know a word
by the company it keeps”
J.R. Firth, 1957

41. “You shall know an asset
by the portfolios it belongs to”
Andrea Gigli, PyCon8, 2017

42. Asset embedding
If word embedding can project words in a vector space taking into account
of the other words along with they are usually accompanied...
… then asset embedding can project assets in a vector space taking
into account of the other assets along with they are usually
accompanied

44. Hands on code now

45. That’s it!
Now you can
- Build a dictionary of dictionaries
- Order and Save your dict() of dict()’s
- Ask for a recommendation
as in the previous application!

46. Conclusions
We wrote the code for two toy-applications of Recommendation Systems
for Banking and Fin Services: one based on graph theory, the other on word
embedding

47. Conclusions
We wrote the code for two toy-applications of Recommendation Systems
for Banking and Fin Services: one based on graph theory, the other on word
embedding
Many more recommendation system can be implemented

48. Conclusions
We wrote the code for two toy-applications of Recommendation Systems
for Banking and Fin Services: one based on graph theory, the other on word
embedding
Many more recommendation system can be implemented
Bear in mind that testing a Recommendation System is not easy!

49. “Cinderella never asked for a prince...
She asked for a dress and a night off.”
Kiera Cass, 2012

50. Thanks!Pycon8
Florence
6th-9th April 2017
Andrea Gigli @andrgig
andrgig@gmail.com

51. Questions?Pycon8
Florence
6th-9th April 2017
Andrea Gigli @andrgig
andrgig@gmail.com