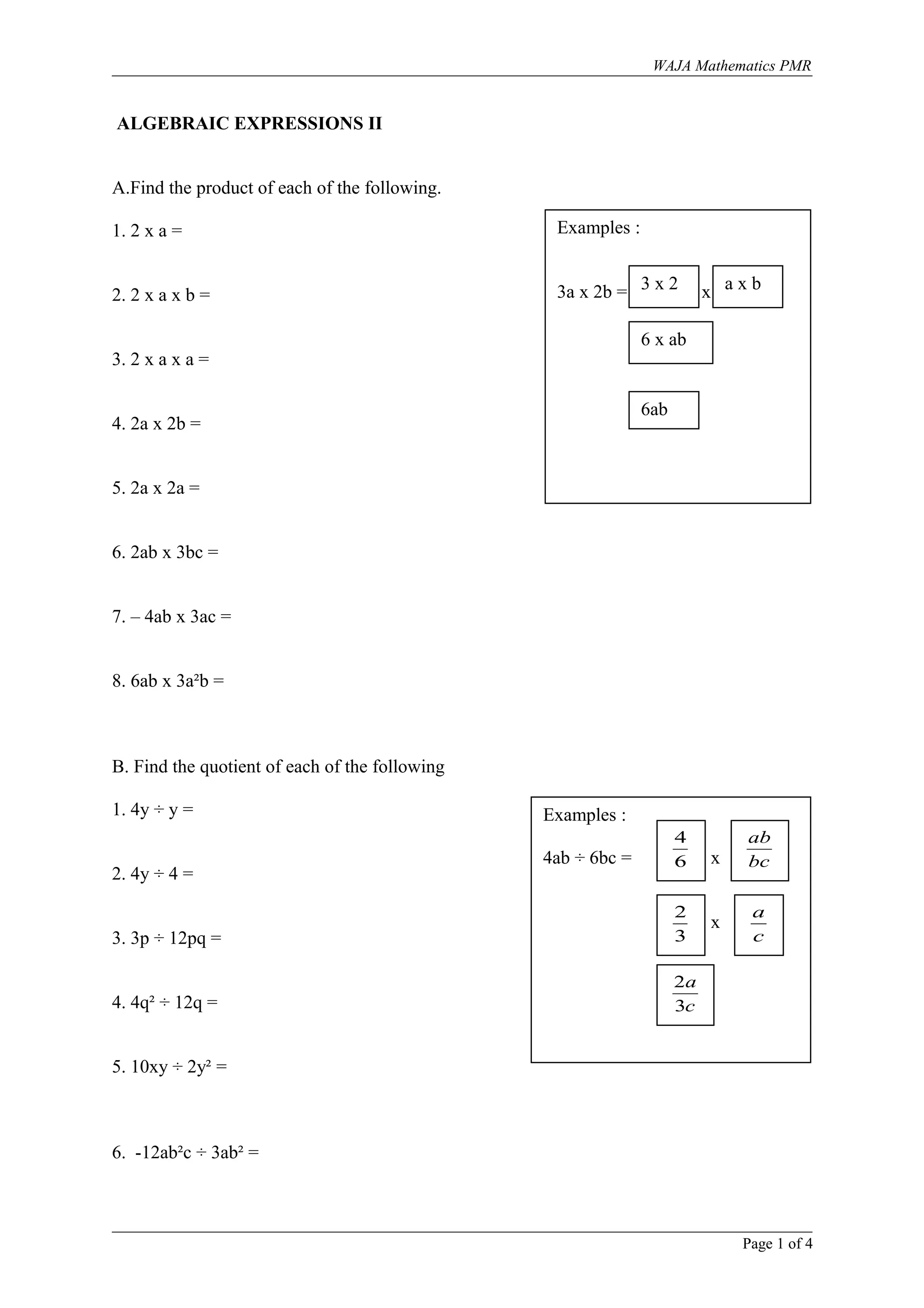
This document provides examples and practice problems for algebraic expressions involving products, quotients, and simplification of expressions with variables. It covers finding products and quotients of expressions with variables. It also covers simplifying expressions by combining like terms, distributing operations, and factoring. The document aims to help students master skills in working with algebraic expressions.

1. WAJA Mathematics PMR
ALGEBRAIC EXPRESSIONS II
A.Find the product of each of the following.
1. 2 x a =
2. 2 x a x b =
3. 2 x a x a =
4. 2a x 2b =
5. 2a x 2a =
6. 2ab x 3bc =
7. – 4ab x 3ac =
8. 6ab x 3a²b =
B. Find the quotient of each of the following
1. 4y ÷ y =
2. 4y ÷ 4 =
3. 3p ÷ 12pq =
4. 4q² ÷ 12q =
5. 10xy ÷ 2y² =
6. -12ab²c ÷ 3ab² =
Page 1 of 4
Examples :
3a x 2b = x3 x 2 a x b
6 x ab
6ab
Examples :
4ab ÷ 6bc = x
x
6
4
bc
ab
3
2
c
a
c
a
3
2

2. WAJA Mathematics PMR
7. – 16xyz² ÷ ( - 8xz² ) =
8. 3abc x 4ab ÷ 12b²c =
C. Simplify each of the following expressions.
1. 8a – 6 =
2. 8a – 6a =
3. 8ab + 5a =
4. 3ab + ab + 2ab =
5. 3xy + 2 + 6xy =
6. 2ab² + ab + ab² - ab =
7. 5w + 2 – 3w =
8. 9m² - 3m – 3m + m² =
9. 4a² - 2ab + 2ab - b² =
10. p² - 6p – 6 – 8 + p =
Page 2 of 4
12
43×
bxbxc
axbxcxaxb
Examples :
9 – 6 = 3
9a – 6 = 9a – 6
9a – 6a = 3a
Examples :
a + a = 2a
a + b = a + b
ab + ab = 2ab
2ab + 3ab = 5ab
xy² + xy = xy² + xy
- 3xy + xy = - 2xy

3. WAJA Mathematics PMR
D. Simplify each of the following.
1. 3(2a – 3b + 4) =
2. -2( x + 2y – z) =
3. 4a( 2a – 2b + 5) =
4. 4x – (2x + 2y) =
5. 3a – 2(a – 3b) =
6.
2
1
( 8a – 6b + 2) =
7.
3
2
( 3x – 6y) =
8. 3( a + 3b) + 2( a – 4b) =
9. 4( x + 3y) – 2( 2x + 5y) =
10. 6( 2p + 3q) – 4( p + 4q) =
Page 3 of 4
Examples :
5(2a -3b + c) = (5 x 2a) – (5 x (-3b)) + (5 x c)
= 10a – 15b + 5c
Examples :
3
2
( 6a – 9) = (
3
2
x 6a) - (
3
2
x 9)
= 4a - 6

4. WAJA Mathematics PMR
Mastering practice
1. q( 2 + p)
2. 3( 2p – 5)
3. q(4p – q)
4. 3( 3m – n) – n( 3m – n)
5. p(p – 3) – 3( p – 3)
6. 2p( 2p – q) – q (2p – q)
7. -3(2y + z – 1)
8. -5a( a + 2b – 3)
9. 3a + 4b – 2(a + 2b)
10. 5xy – 3x² - x(3x +4y)
Page 4 of 4