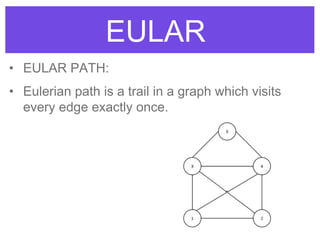
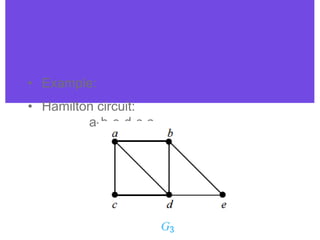
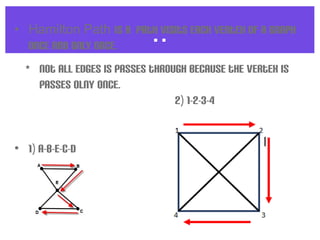
An Euler circuit is a trail that starts and ends at the same vertex and uses every edge in a graph exactly once. An Euler path starts and ends at different vertices and uses every edge once but may not visit every vertex. To determine if a graph contains an Euler circuit or path, one checks if every vertex has an even degree; if so, it contains an Euler circuit. For an Euler path, exactly two vertices may have an odd degree. Algorithms for finding these trails include picking a starting vertex and traversing edges, darkening used edges until all are traversed. A Hamilton circuit is similar but visits every vertex exactly once, returning to the starting point. A Hamilton path visits each vertex once without returning to the starting point

1. tree
TAF 3053

2. EULAR
• EULAR PATH:
• Eulerian path is a trail in a graph which visits
every edge exactly once.

3. ....• EULAR CIRCUIT
An Euler circuit is a circuit that uses every edge of
a graph exactly once.
• I An Euler circuit starts and ends at the same
vertex.

4. 2. Determine what are the properties that
differentiate between a and b in Question 1?
• EULAR PATH:
• Starting at initial vertex and ending at other vertex.
• Some degree vertex are odd.
• Odd degree vertex => 2.
• EULAR CIRCUIT:
• Starting with initial vertex and ending at initial vertex.
• All degree vertex are even.

5. 3. What are the algorithm or step
by step to determine a and b in
Question 1?
• Euler Path :
•  Pick any vertex to start
•  From that vertex pick an edge to traverse
•  Darken that edge, as a reminder that you can't
traverse it again
•  Travel that edge, coming to the next vertex
•  Repeat 2-4 until all edges have been traversed, and
you are back at the starting vertex

6. ...• Euler Circuit
•  Step One: Randomly moves from node to node, until
stuck. Since all nodes had even degree, the circuit must
have stopped at its starting point. (It is a circuit.)
•  Step Two: If any of the arcs have not been included in
our circuit, find an arc that touches our partial circuit,
and add in a new circuit.
•  Each time we add a new circuit, we have included more
nodes.
•  Since there are only a finite number of nodes,
eventually the whole graph is included.

7. • Example:
• Hamilton circuit:
a-b-e-d-c-a

8. ..• Hamilton Path is a path visits each vertex of a graph
once and only once.
• Not all edges is passes through because the vertex is
passes olny once.
2) 1-2-3-4
• 1) A-B-E-C-D

9. 5. Determine what are the
properties that differentiate
between a and b in Question 4?
• HAMILTON CIRCUIT:
• When this initial vertex is connected to each
vertex until it meet the end at initial vertex
• HAMILTON PATH:
• The initial vertex is connected each vertex
until it meet the last vertex before initial
vertex

10. 6. What are the algorithm or step
by step to determine a and b in
Question 4?
• TO DETERMINE HAMILTON CIRCUIT
• DIRAC’S THEOREM: If G is a simple graph with n vertices with
n 3 such that the≥
• degree of every vertex in G is at least n/2, then G has a
Hamilton circuit
• ORE’S THEOREM : If G is a simple graph with n vertices with n
3 such that≥
• deg(u) + deg(v) n for every pair of nonadjacent vertices u≥
and v in G, then G has a Hamilton circuit.

11. `• Randomized algorithm
• A randomized algorithm for Hamiltonian path
that is fast on most graphs is the following:
Start from a random vertex, and continue if
there is a neighbor not visited. If there are no
more unvisited neighbors, and the path formed
isn't Hamiltonian, pick a neighbor uniformly at
random, and rotate using that neighbor as a
pivot. (That is, add an edge to that neighbor, and
remove one of the existing edges from that
neighbor so as not to form a loop.) Then, continue
the algorithm at the new end of the path.

12. `