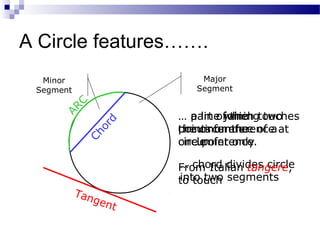
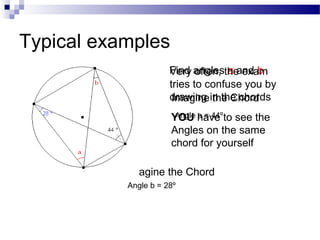
This document defines and explains several circle theorems and properties. It defines key circle terms like diameter, radius, chord, arc, tangent, and segment. It then explains four properties of angles in circles: (1) angles subtended by the same chord or arc in the same segment are equal; (2) if two angles stand on the same chord, the angle at the center is twice the angle at the circumference; (3) the angle in a semi-circle is a right angle; and (4) opposite angles in a cyclic quadrilateral add up to 180 degrees. It also defines properties of tangents to circles, such as tangents being perpendicular to radii and tangents from an outside point being equal.

1. Circle Theorems

2. A Circle features…….
… the distance around
the Circle…
… its PERIMETER
Diameter
… the distance across
the circle, passing
through the centre of
the circle
Radius
… the distance from
the centre of the circle
to any point on the
circumference

3. A Circle features…….
… a line joining two
points on the
circumference.
… chord divides circle
into two segments
… part of the
circumference of a
circle
Chord
Tangent
Major
Segment
Minor
Segment
ARC
… a line which touches
the circumference at
one point only
From Italian tangere,
to touch

4. Properties of circles
 When angles, triangles and quadrilaterals
are constructed in a circle, the angles
have certain properties
 We are going to look at 4 such properties
before trying out some questions together

5. An ANGLE on a chord
An angle that ‘sits’ on a
chord does not change as
the APEX moves around
the circumference
… as long as it stays
in the same segment
We say “Angles
subtended by a chord
in the same segment
are equal”
Alternatively “Angles
subtended by an arc
in the same segment
are equal”
From now on, we will only consider the CHORD, not the ARC

6. Typical examples
Find angles a and b
Imagine the Chord
Angle b = 28º
Imagine the Chord
Angle a = 44º
Very often, the exam
tries to confuse you by
drawing in the chords
YOU have to see the
Angles on the same
chord for yourself

7. Angle at the centre
Consider the two angles
which stand on this
same chord
Chord
What do you notice
about the angle at the
circumference?
It is half the angle at the
centre
We say “If two angles stand on the same chord,
then the angle at the centre is twice the angle at
the circumference”
A

8. Angle at the centre
We say “If two angles stand on the same chord,
then the angle at the centre is twice the angle at
the circumference”
It’s still true when we move
The apex, A, around the
circumference
A
As long as it stays in the
same segment
136°
272°
Of course, the reflex angle
at the centre is twice the
angle at circumference too!!

9. Angle at Centre
A Special Case
When the angle stands
on the diameter, what is
the size of angle a?
aa
The diameter is a straight
line so the angle at the
centre is 180°
Angle a = 90°
We say “The angle in a semi-circle is a Right Angle”

10. A Cyclic Quadrilateral
…is a Quadrilateral
whose vertices lie on the
circumference of a circle
Opposite angles in a
Cyclic Quadrilateral
Add up to 180°
They are supplementary
We say
“Opposite angles in a cyclic quadrilateral add up to 180°”

11. Questions

15. Could you define a rule for this situation?

16. Tangents
 When a tangent to a circle is drawn, the
angles inside & outside the circle have
several properties.

17. 1. Tangent & Radius
A tangent is perpendicular
to the radius of a circle

18. 2. Two tangents from a point outside circle
PA = PB
Tangents are equal
PO bisects angle APB
g
g
<PAO = <PBO = 90°90°
90°
<APO = <BPO
AO = BO (Radii)
The two Triangles APO and BPO are Congruent

19. 3 Alternate Segment Theorem
The angle between a tangent
and a chord is equal to any
Angle in the alternate segment
Angle between tangent & chord
Alternate Segment
Angle in Alternate Segment
We say
“The angle between a tangent and a chord is equal to any
Angle in the alternate (opposite) segment”