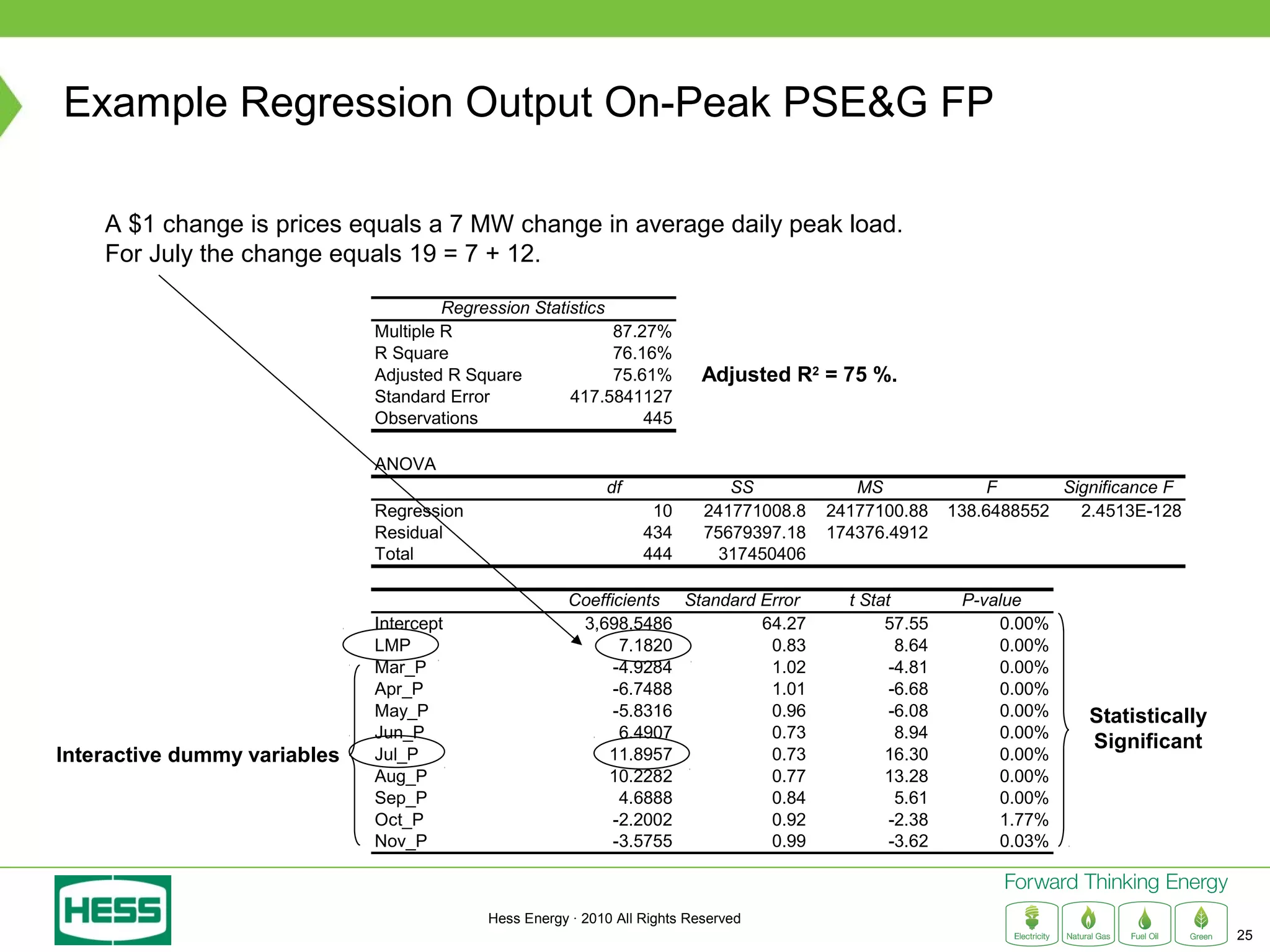
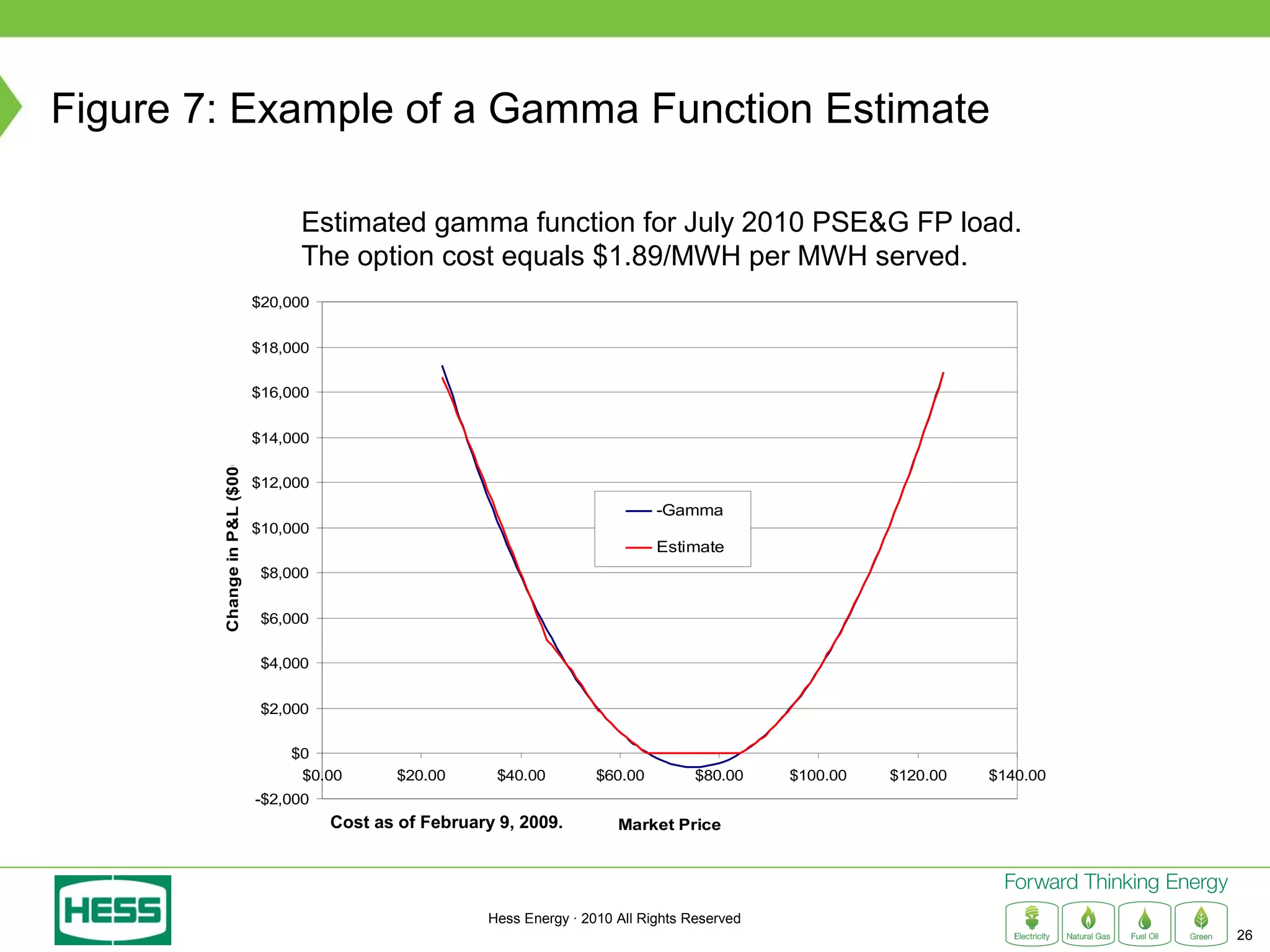
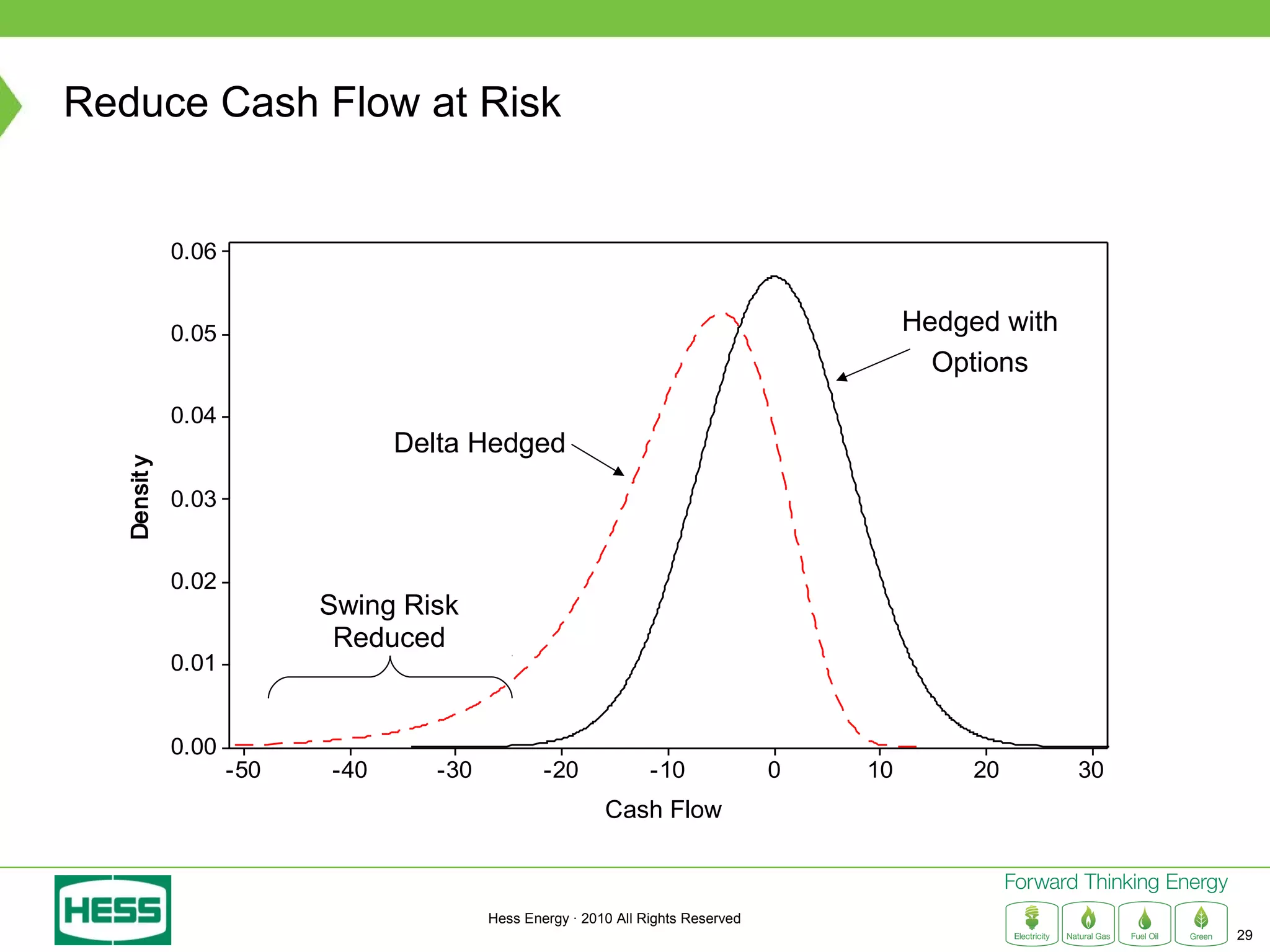
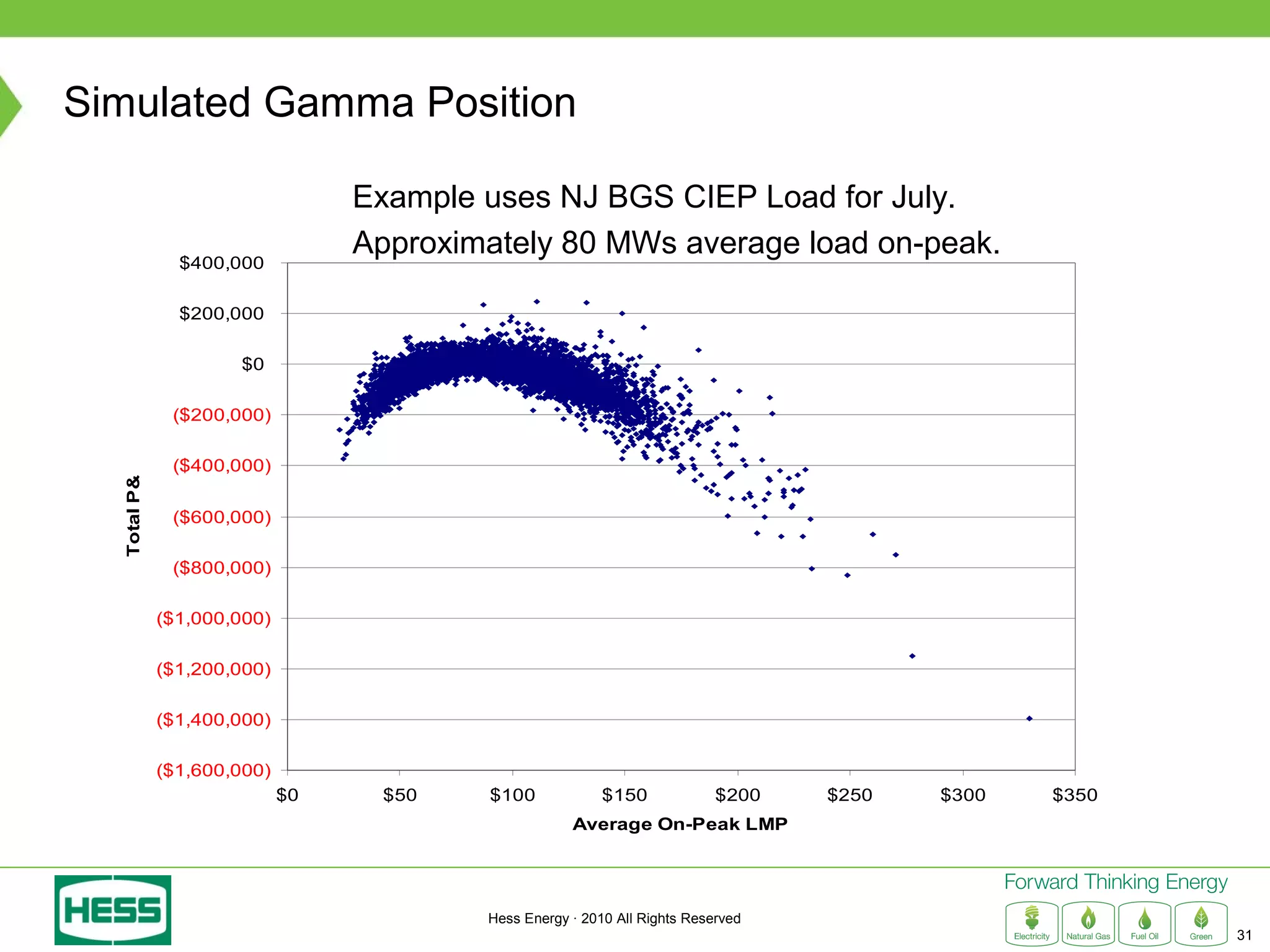
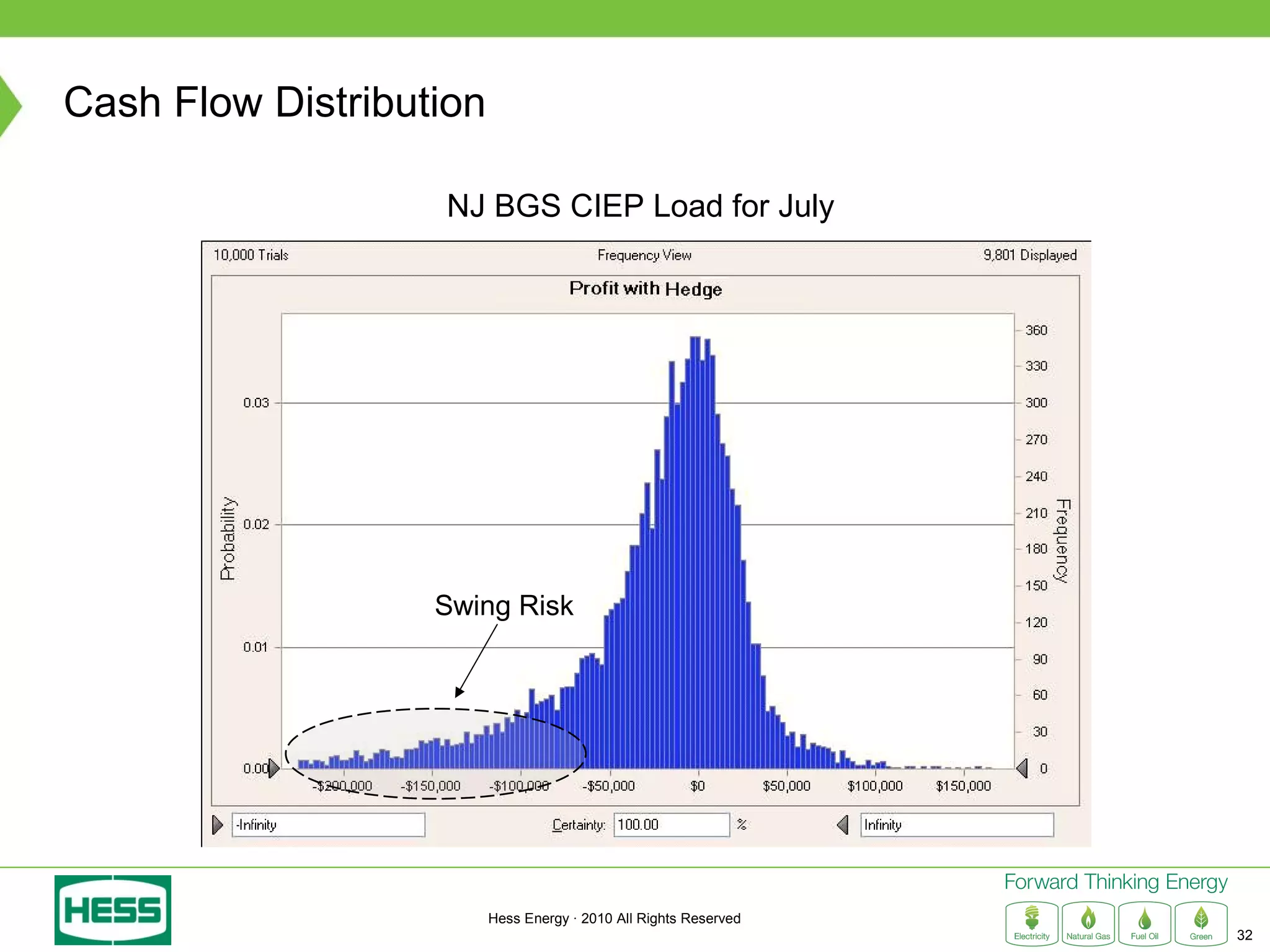
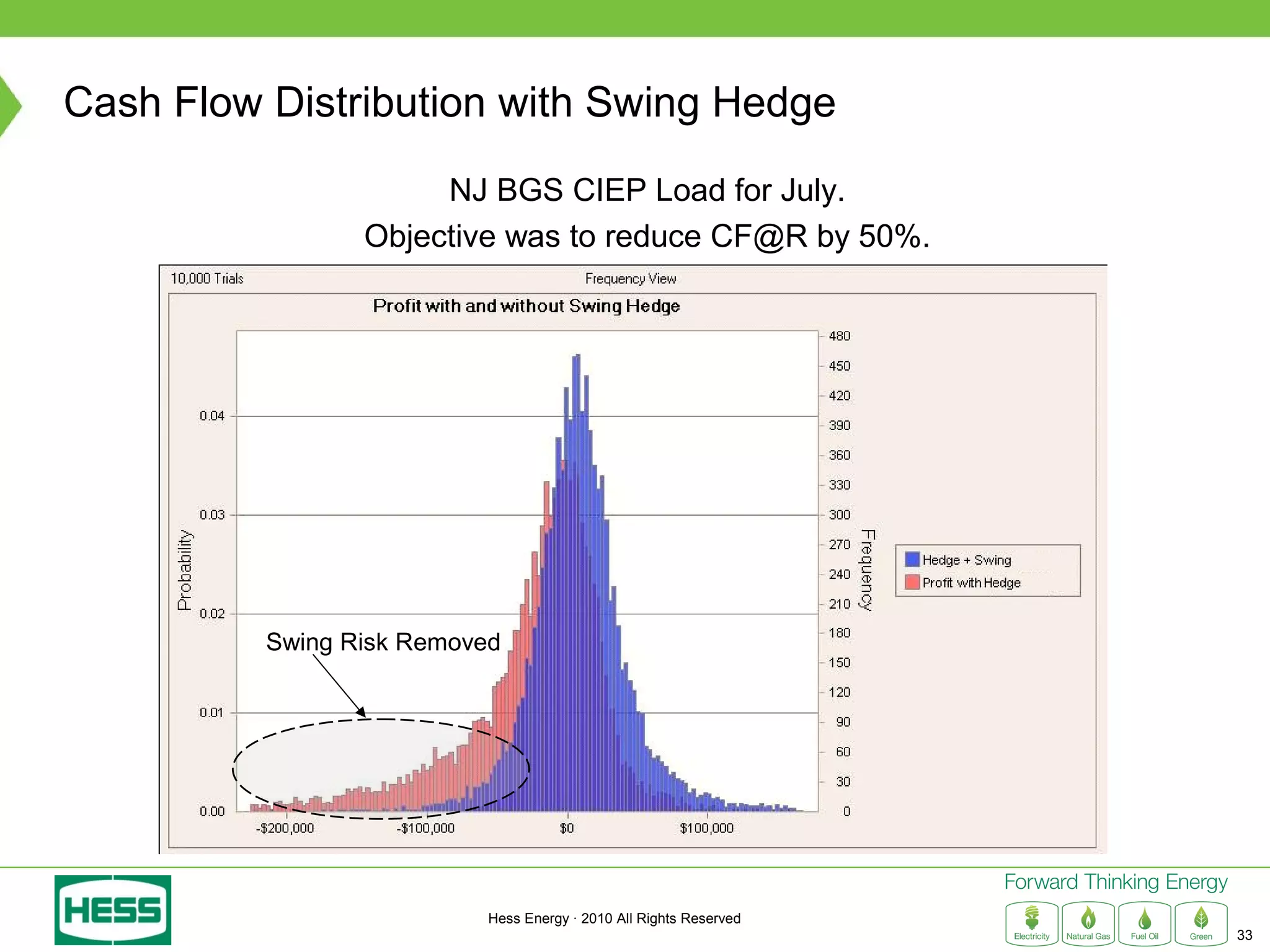
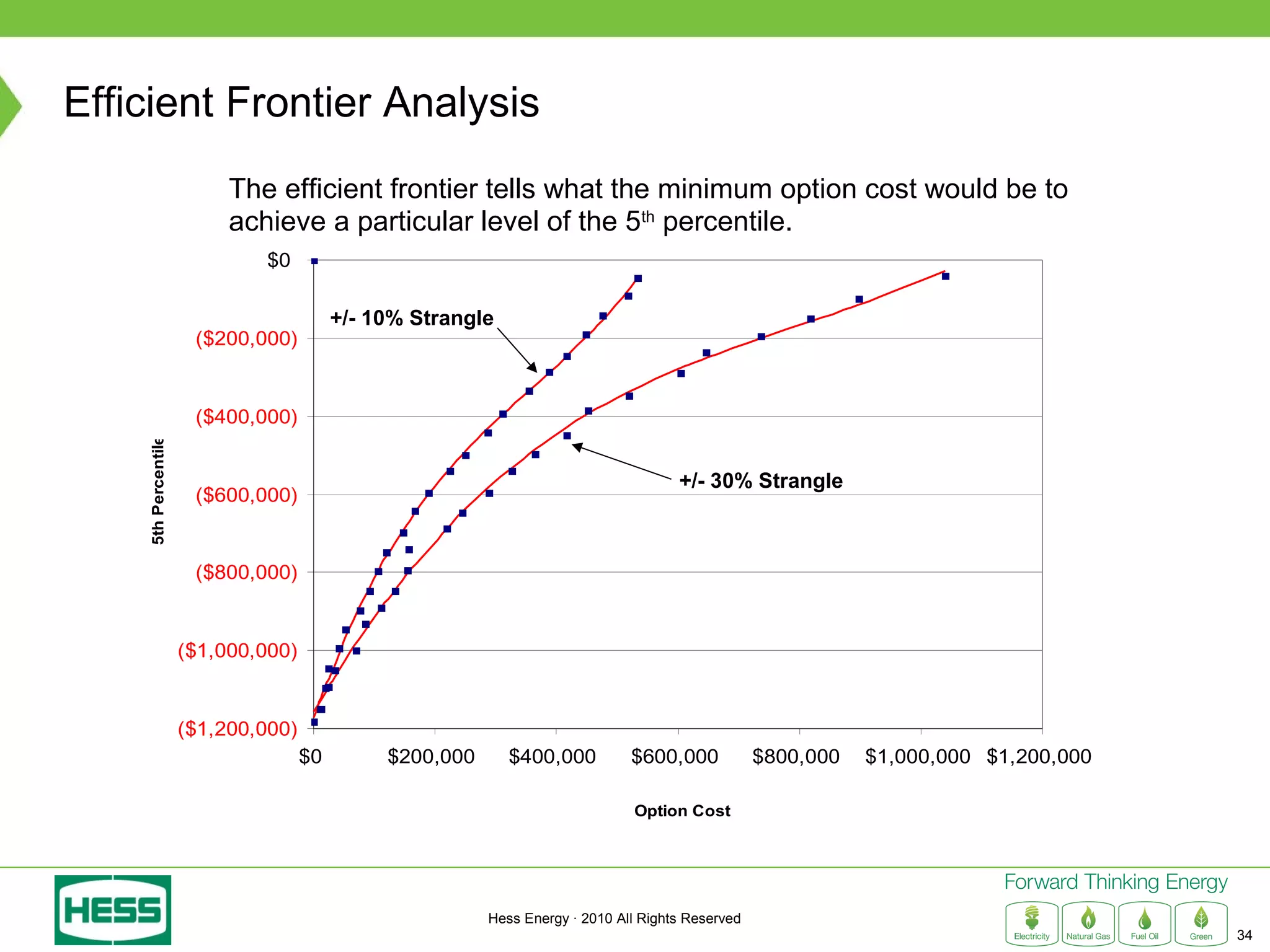
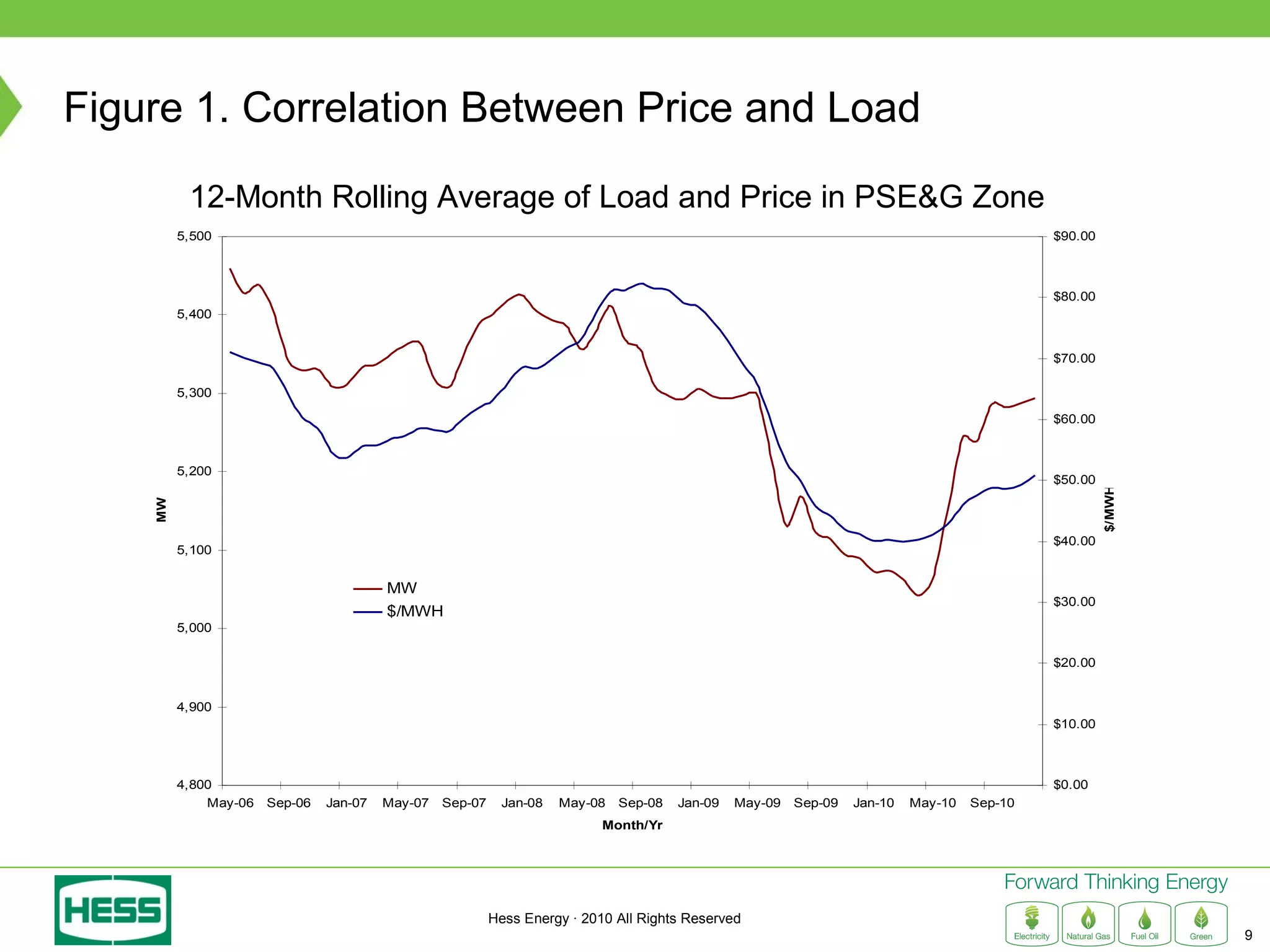
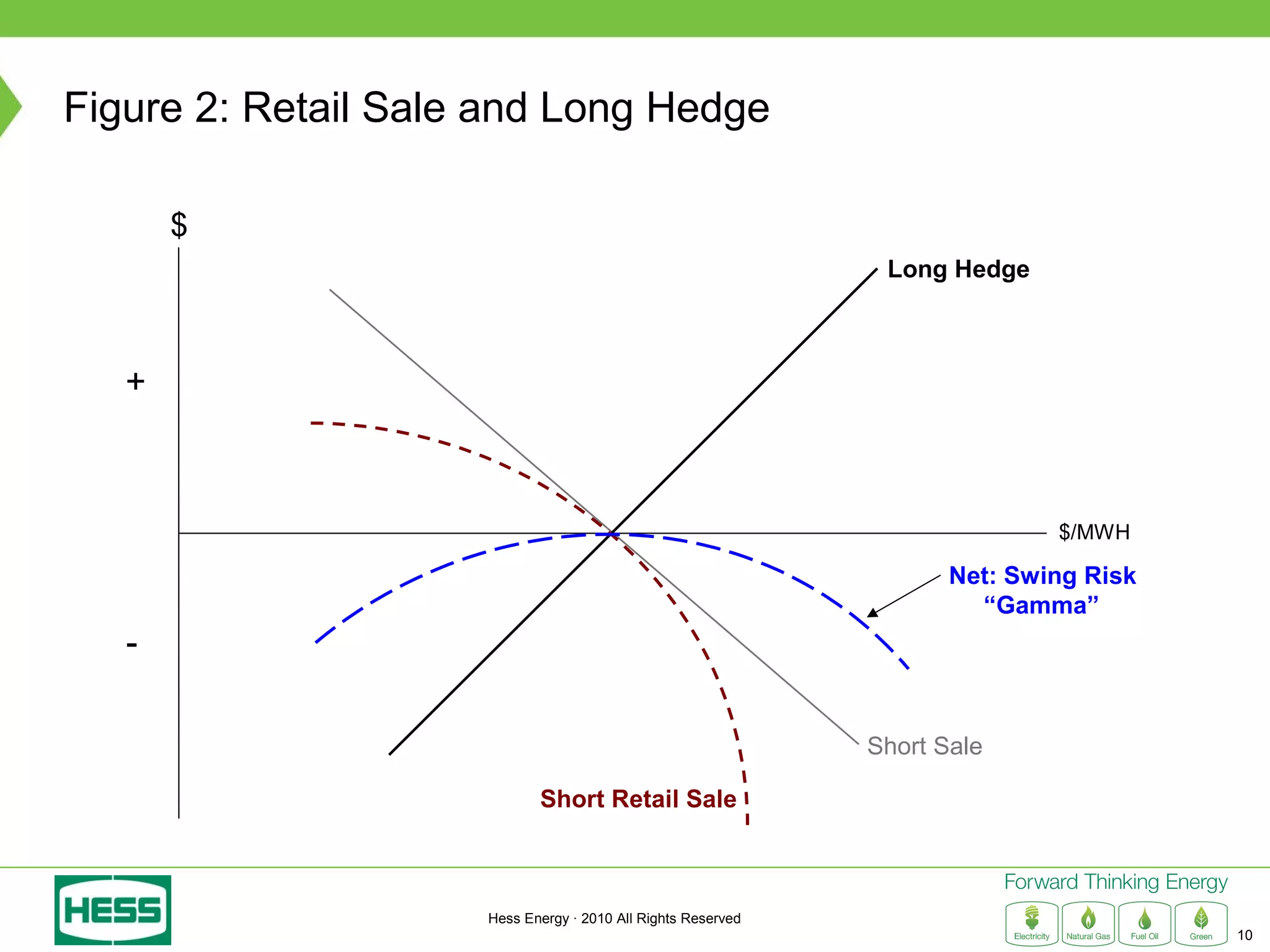
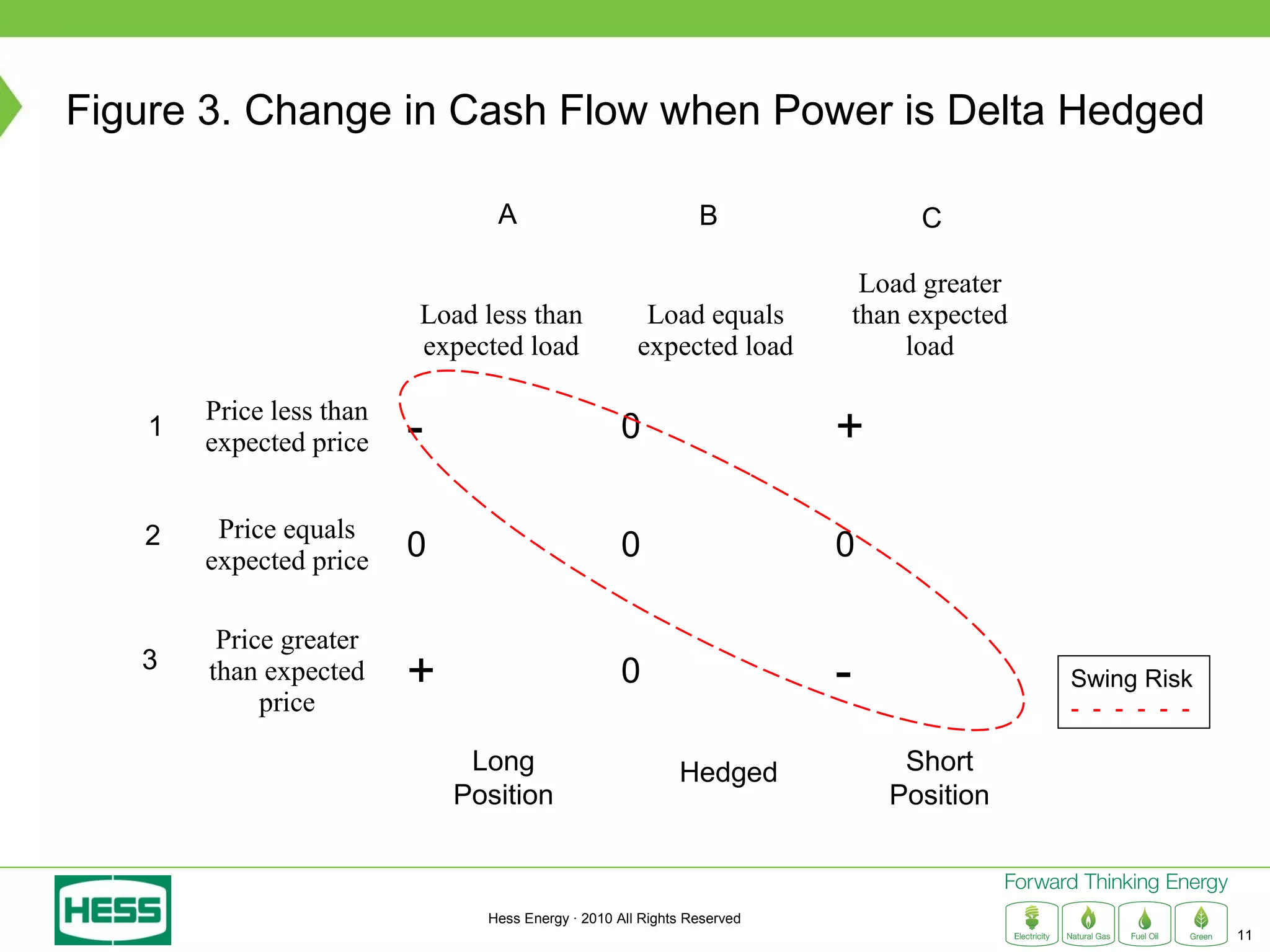
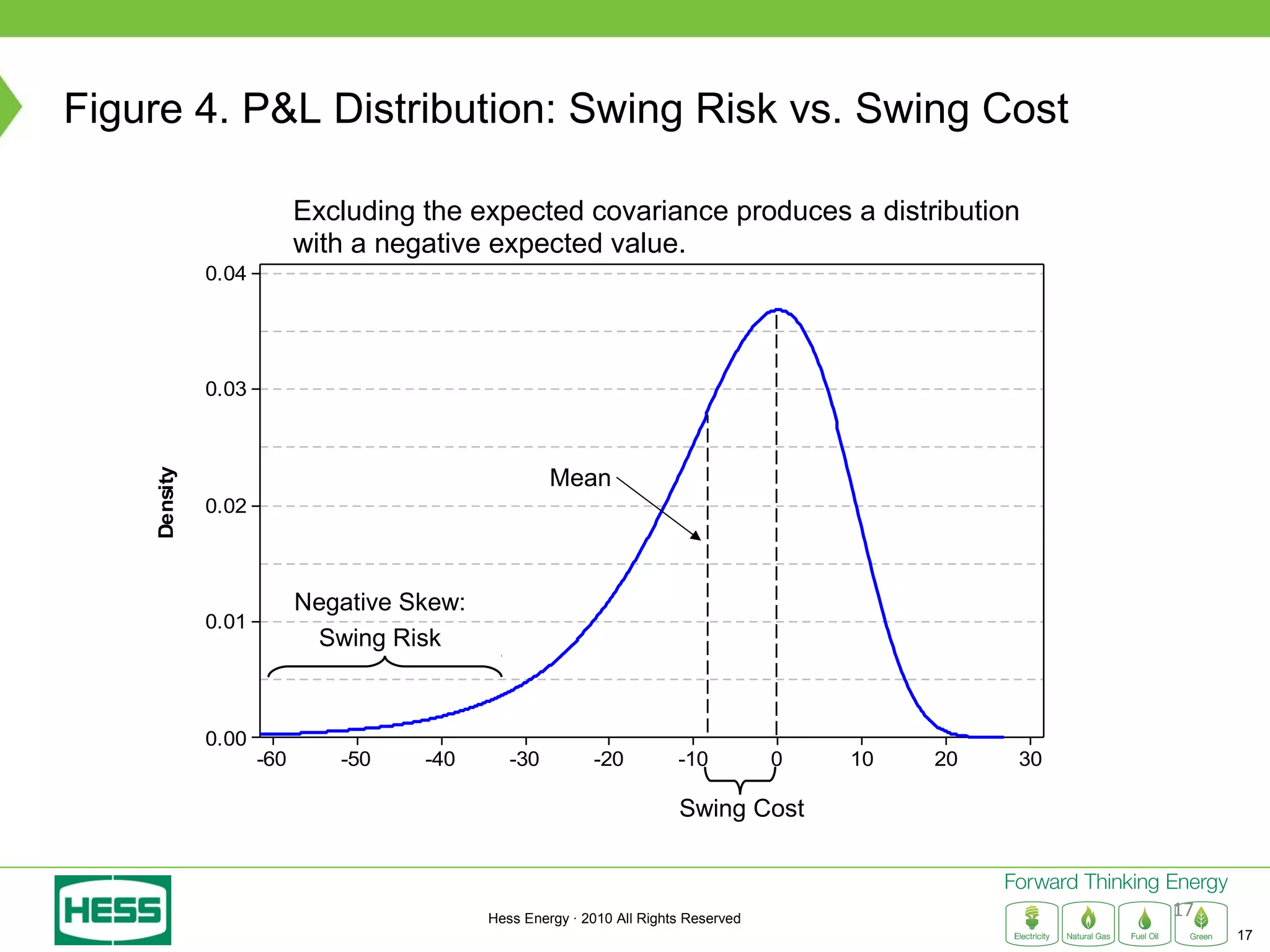
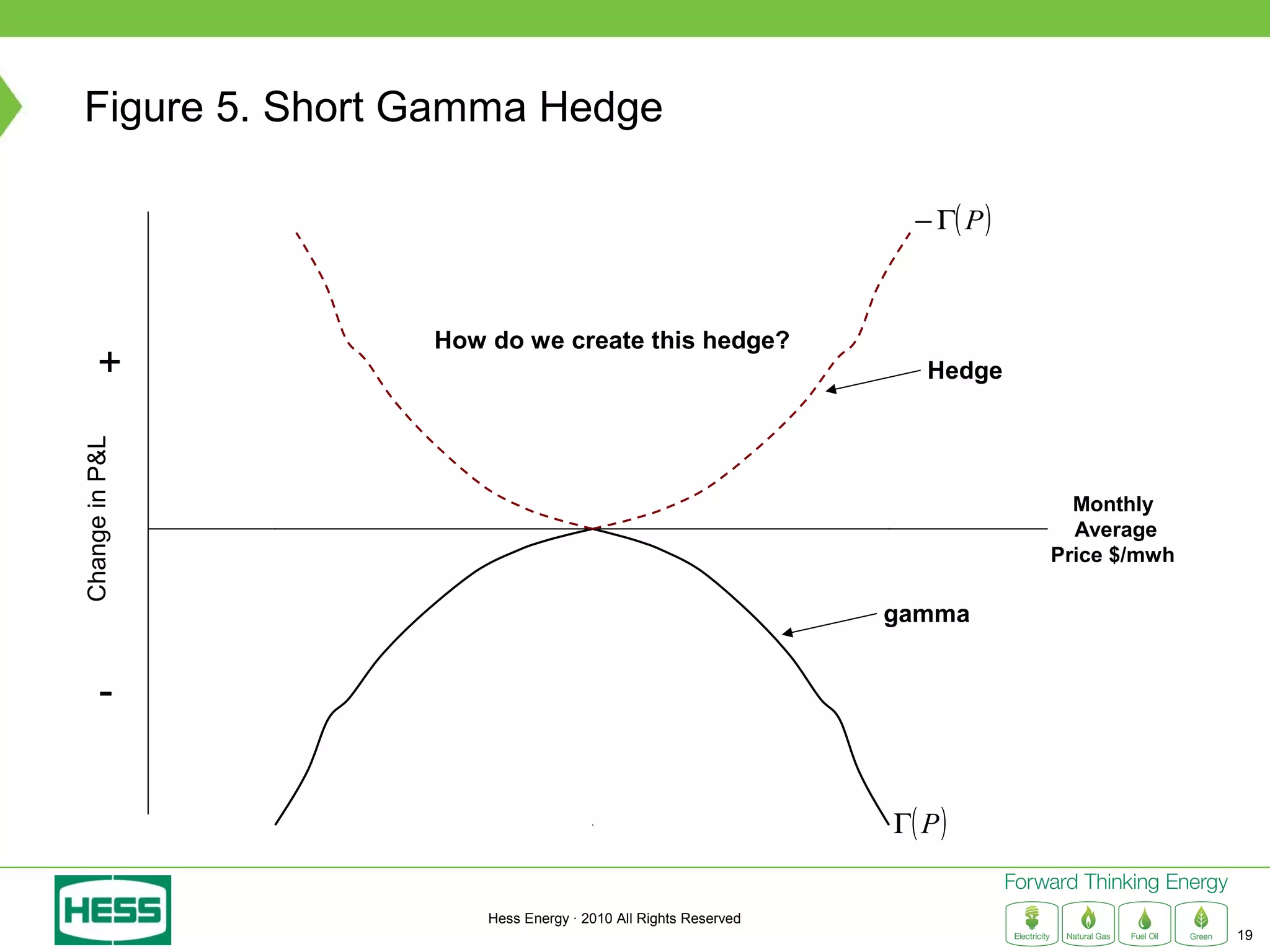
Modeling and Hedging the Risk in Retail Load Contracts

Modeling and Hedging the Risk in Retail
Load Contracts
Eric Meerdink, Director of Structuring & Analytics

May 3, 2011

Hess Energy · 2010 All Rights Reserved
1

Background on Hess Corporation

2

Hess: Who We are Today
A Totally Integrated Energy Company
RETAIL MARKETING
ENERGY TRADING
Selling motor fuels and
REFINING Hess Energy Trading
convenience products at
EXPLORATION Processing the Company, a joint
retail stores
Discovering oil crude oil into venture buying and
and gas finished products selling energy financial
instruments

ENERGY
MARKETING
Marketing petroleum
SUPPLY, TRADING & products, natural gas
PRODUCTION & TRANSPORTATION TERMINALS and electricity to
DEVELOPMENT Buying, selling and Storing products and commercial,
Getting crude oil out of transporting crude oil and distributing fuels to our industrial and utility
the ground finished products customers customers

3

One of the Largest Energy Suppliers on the East Coast

4

Hess Energy: Robust Product Suite

Electricity Natural Gas Fuel Oil Green Suite

Marketing to Marketing to Delivery to Commercial Reducing electric
Commercial & Commercial & & Industrial customers usage during times of
Industrial customers Industrial customers peak demand
Distributor sales from
4,500 MWs/hr (RTC ) Wholesale to LDCs Hess terminals Support renewable
(enough electricity to energy sources, such
power 4 million 1.5 BCF/day 110K BPD as wind, solar, biomass
average homes) and hydropower

#2 electric marketer on Balance your carbon
the east coast impact from oil and
natural gas with carbon
offsets

5

Volumetric Risk in Retail Load Contracts

6

What is a Full Requirements Load Following Contract

• Full Requirements Load Following: A fixed price agreement to serve all
the electricity load of a customer, and provide all products required to
supply the electric load, for a pre-determined interval of time, without
restrictions on volume. Typically served at a fixed rate per MWH.

• Also called Full Plant Requirements Contract.

• Typical key products to be supplied:
○ Load Following Energy
○ Capacity
○ Transmission
○ Ancillaries
○ RECs

7

Volumetric or Swing Risk

• Volumetric or swing risk is defined as a cash flow risk caused by
deviations in delivered volumes compared to expected volumes. The
primary cause of these volumetric deviations is weather and economic
conditions.
• Not enough that delivered volumes deviate from expected volumes.
○ These deviations in delivered volumes must be positively correlated with
market prices.
○ The full requirements load following contract is delta hedged at some
expected volume.
• Under these conditions the resulting expected cash flow position is
negative and non-linear with respect to changes in market prices.
• Swing risk is similar to the gamma position of an option, as it is a second
order price risk.

8

Figure 1. Correlation Between Price and Load

12-Month Rolling Average of Load and Price in PSE&G Zone
5,500 $90.00

$80.00
5,400

$70.00

5,300

$60.00

5,200
$50.00

$/MWH
MW

$40.00
5,100

MW
$30.00
$/MWH
5,000

$20.00

4,900
$10.00

4,800 $0.00
May-06 Sep-06 Jan-07 May-07 Sep-07 Jan-08 May-08 Sep-08 Jan-09 May-09 Sep-09 Jan-10 May-10 Sep-10
Month/Yr

9

Figure 2: Retail Sale and Long Hedge

$
Long Hedge

+

$/MWH

Net: Swing Risk
“Gamma”
-

Short Sale

Short Retail Sale

10

Figure 3. Change in Cash Flow when Power is Delta Hedged

A B C

Load greater
Load less than Load equals than expected
expected load expected load load

Price less than
1
expected price - 0 +

2 Price equals
expected price 0 0 0

Price greater
3 than expected
price
+ 0 - Swing Risk
- - - - - -

Long Hedged Short
Position Position

11

Expected Cost to Serve Load
and Swing Risk

12


• Model assumptions:
○ Pi = Actual price in hour i (random variable)
○ Li = Actual load in hour i (random variable)
○ Covi = Covariance between P and L in hour i Cov(Pi,Li).
○ i = hours in the month i = 1,…,N
○ Averages will be denoted with a bar over the variable
○ Expectations will be taken at time t given information available up to and
including time t. Referenced by a subscript t.
N
1
Pt =
N
∑P
i =1
t
i
= Forward Value of Power

N
1
Lt =
N
∑L
i =1
i
t = Forward Value of Expected Load

13


N
• Cost to serve load: Cost = ∑P L
i =1
i i

 N i i
• Expected cost to serve load : Et ( Cost ) = Et  P L 

 i =1


∑
• Taking expectations and solving we get:
Expected block Expected load Expected covariance
cost of power. shaping cost. between price and load.

∑(L )
N N
(1 Et ( Cost ) = N ⋅ Pt ⋅ Lt +
)
i =1
i
t − L Pti +
t ∑Cov ( P , L )
i =1
i i

( 2) Et ( Cost ) = (1 + SFt ) Pt N Lt
SF = Shaping Factor. Ratio of the sum of the
expected load shaping cost and expected covariance
cost to the expected block cost.

14

Hedging the Expected Cost
• Start with the expected cost function, equation (1) and take a Taylor series
expansion with respect to prices and loads.
N
∂Cti ∂Cti i
(3) ∆Costt = ∑( )
i =1
Lit ∆Pti + ∆Lit ( )
Pti + i ∆Pt + i ∆Lt + 
∂Pt
i
∂Lt

• Where  refers to higher order terms. Neglecting these terms we can write
the change in expected cost as:

 ∂Pti ∂Cti ∂Pti   N  i ∂Cti  ∂Lit 
∑( )
N
=  N ⋅ Lt +


Lit − Lt + i
∂Pt ∂Pt ∂Pt 
 ∆Pt +   Pt + i

  ∂Lt
∑ 
 ∂L
 ∆Lt

(3)
i =1  i =1   t 

Price Hedge Load Hedge
The delta on a load following After delta hedging the price risk
contract does not equal 1.0 we are left with the first order load risk
or Gamma risk.

15

Fair Value of a Load Following Contract

• A fair price or fair value contract has an expected value of zero.
• Fair value contracts require the inclusion of the expected value of the
covariance between price and load, not just the expected hourly shaping
cost. Excluding this cost component biases the distribution to the left.
• But inclusion of the expected covariance in the contract price does not
guarantee that the swing risk has been minimized or removed. It only
guarantees that the contract is priced fairly.
• We are still left with the negative tail risk from large positively correlated
price and load movements – Cash Flow at Risk.

16

Figure 4. P&L Distribution: Swing Risk vs. Swing Cost

Excluding the expected covariance produces a distribution
with a negative expected value.
0.04

0.03

Mean
Density

0.02

Negative Skew:
0.01
Swing Risk

0.00
-60 -50 -40 -30 -20 -10 0 10 20 30

Cash Flow
Swing Cost

Hess Energy · 2010 All Rights Reserved 17
17

Option Hedge Development

18

Figure 5. Short Gamma Hedge

− Γ( P )

How do we create this hedge?
+ Hedge
Change in P&L

Monthly
Average
Price $/mwh

gamma

-

Γ( P )

19

Figure 6. Creating a Gamma Position from Options

Use vanilla calls and puts to construct the gamma position.

− Γ( P )
+
− Γ( P )
ˆ
Change in P&L

Monthly
Average
Price $/mwh
-

20

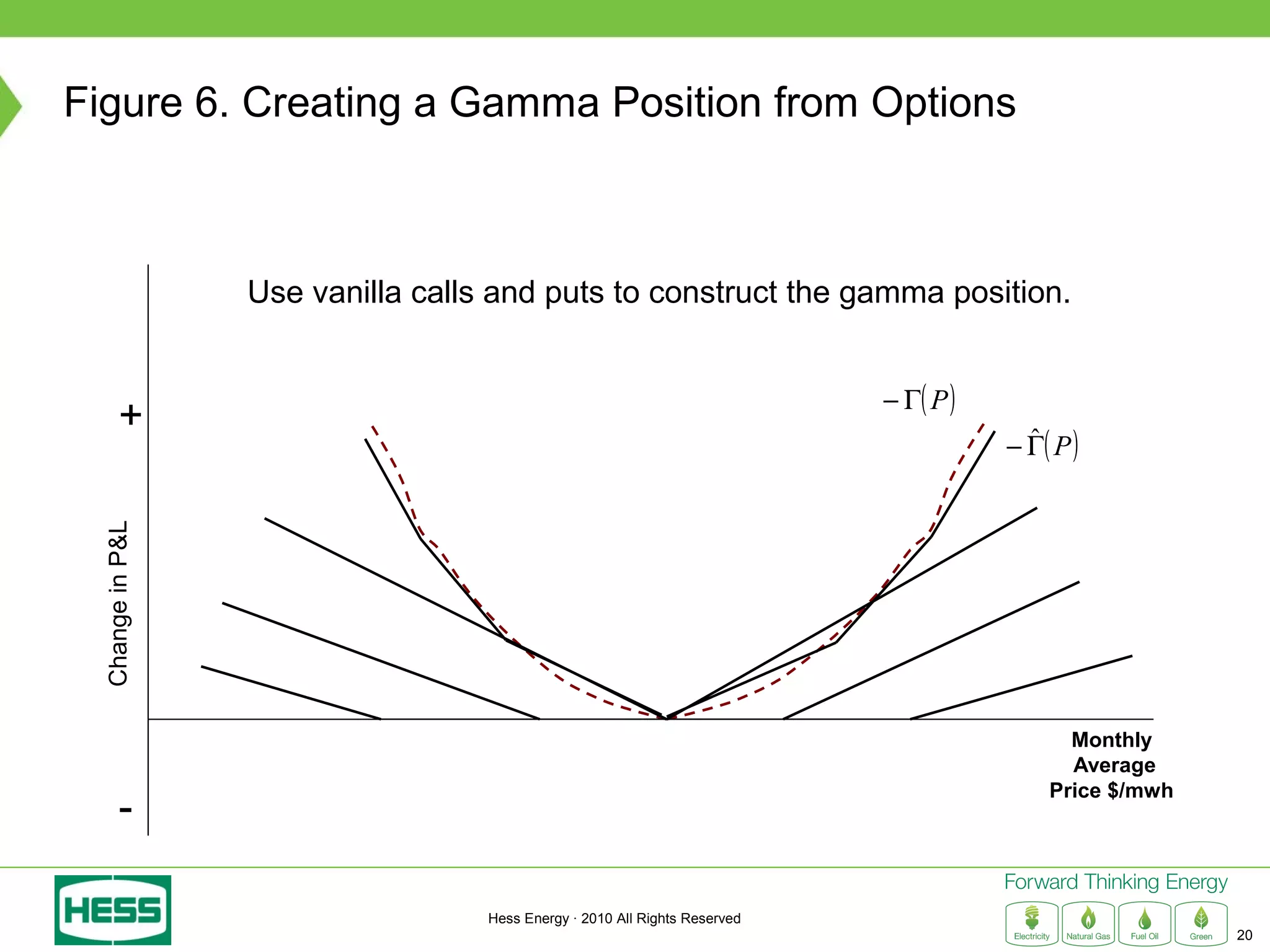
Solving for the Estimated Gamma Function

• Select a series of strikes, Ki , and quantities, θi, to create a portfolio of
puts and calls.
• To estimate the gamma function we need to choose the amount of
options for each strike, θi , so as to minimize the distance between the
estimated gamma function and the true gamma function.
• Estimated gamma function equals:
N M
− Γ( P ) =
ˆ
∑Max( P − K , 0) ×θ + ∑Max( K
i =1
i i
i =1
i − P,0 ) ×θi

• Choose the optimal quantities by minimizing the sum of the squared
errors between the true and estimated gamma function over a set of Q
prices. 2

∑ [Γ( P ) − Γ( P )]
Q
min ˆ j j
θ
j =1

21

Theoretical Model

• It has been shown that a static hedge of plain vanilla options and
forwards can be used to replicate any European derivative (Carr and
Chou 2002, Carr and Madan 2001).
• Any twice continuously differentiable payoff function, f (S ), of the
terminal price S can be written as:
F0 ∞
f ( S ) = f ( F0 ) + f ′( F0 )( S − F0 ) + ∫ f ′′( K )( K − S ) dK ++
∫ f ′′( K )( S − K ) + dK
0 F0

Initial Delta
Gamma Hedge: “Swing Risk”
P&L Position

• Our payoff function is the terminal profit. It can be decomposed into a
static position in the day 1 P&L, initially costless forward contracts,
and a continuum of out-of-the-money options. F0 is the initial forward
price.

22

Theoretical Model, Cont.

• The initial value of the payoff must be the cost of the replicating
portfolio.
F0 ∞
V0 ( F0 ) = f ( F0 ) e −rT
+ ∫ f ′′( K ) P ( K , T ) dK + ∫ f ′′( K ) C ( K , T ) dK
0 F0

• Where P(K,T) and C(K,T) are the initial values of out-of-the-money
puts and calls respectively.
• Interpretation of term within the integral: Second derivative of the
payoff function representing the quantity of options bought or sold.
○ R = Fixed revenue rate
○ SF = Shaping Factor
○ L(S) = MWH, function of S (spot price of power)

f ( S ) = ( R − (1 + SF ) S ) L( S )

f ′′( K ) = 2 (1 + SF ) ∂L
∂S

23

Estimating the Gamma Function

• Need to estimate the relationship between load and price.
• Use historic data to estimate the following regression equation.
11 11
Load t = α + β lmpt + ∑λ D + ∑φ D lmp
i =1
i i
i =1
i i t

• The data for this equation is average load (peak, off-peak) and average price
(peak, off-peak). LMP is the price, D is a monthly dummy variable, and DXLMP
is an interactive dummy variable with price.
• Next set up a portfolio of a short load sale and a long hedge using monthly
forwards. The fixed rate on the load sale equals the RTC cost of serving the
load ($/MWH).
• Use the relationship estimated in the regression equation to vary the average
monthly load with respect to a change in average monthly price. Use this to
estimate the gamma function.

24

Example Regression Output On-Peak PSE&G FP

A $1 change is prices equals a 7 MW change in average daily peak load.
For July the change equals 19 = 7 + 12.

Regression Statistics
Multiple R 87.27%
R Square 76.16%
Adjusted R Square 75.61% Adjusted R2 = 75 %.
Standard Error 417.5841127
Observations 445

ANOVA
df SS MS F Significance F
Regression 10 241771008.8 24177100.88 138.6488552 2.4513E-128
Residual 434 75679397.18 174376.4912
Total 444 317450406

Coefficients Standard Error t Stat P-value
Intercept 3,698.5486 64.27 57.55 0.00%
LMP 7.1820 0.83 8.64 0.00%
Mar_P -4.9284 1.02 -4.81 0.00%
Apr_P -6.7488 1.01 -6.68 0.00%
May_P -5.8316 0.96 -6.08 0.00% Statistically
Jun_P 6.4907 0.73 8.94 0.00%
Significant
Interactive dummy variables Jul_P 11.8957 0.73 16.30 0.00%
Aug_P 10.2282 0.77 13.28 0.00%
Sep_P 4.6888 0.84 5.61 0.00%
Oct_P -2.2002 0.92 -2.38 1.77%
Nov_P -3.5755 0.99 -3.62 0.03%

25

Figure 7: Example of a Gamma Function Estimate

Estimated gamma function for July 2010 PSE&G FP load.
The option cost equals $1.89/MWH per MWH served.
$20,000

$18,000

$16,000

$14,000
Change in P&L ($000)

$12,000
-Gamma
$10,000
Estimate
$8,000

$6,000

$4,000

$2,000

$0
$0.00 $20.00 $40.00 $60.00 $80.00 $100.00 $120.00 $140.00
-$2,000
Cost as of February 9, 2009. Market Price

26

Mitigating Swing Risk in Practice

“In theory there is no difference between theory and practice.
In practice there is” Yogi Berra

27

Minimizing Cash Flow at Risk

• In practice we cannot purchase options in such a way as to create the
smooth curves depicted earlier. Instead we need to find discrete strikes
so as to minimize the “swing risk”.
• Swing risk is here defined as Cash Flow at Risk (CF@R). CF@R is the
expected loss assuming that all contracts are taken to delivery. I am
defining CF@R as the difference between the mean of the distribution
and the 5th percentile.
• Since we cannot perfectly hedge the swing risk by purchasing a
continuum of options we need another objective risk minimization
strategy.
• Use as a strategy the minimization of the CF@R or an objective level for
the CF@R. An example would be to reduce the CF@R by 50%.

28

Reduce Cash Flow at Risk

0.06
Accountnig or Actuarial w ith Options

0.05
Accounting Model Hedged with
Options
0.04
Delta Hedged
Densit y

0.03

0.02
Swing Risk
Reduced
0.01

0.00
-50 -40 -30 -20 -10 0 10 20 30
CashXFlow

29

Methodology

• Use Monte Carlo simulation to model the load following contract and all
hedges.
• Model takes into account the relationship between price and load,
volatilities and correlations.
• Run the model to estimate the expected cost to serve the load and
establish the fair price of the contract.
• Layer in delta hedges to estimate the cash flow distribution and estimate
the CF@R.
• Determine the amount of risk to be minimized. This is a management
decision. Cut the CF@R by 50%.
• Determine the portfolio of available options in the market.
• Use an available optimization routine to determine the optimal option
portfolio that meets the required risk criteria.

30

Simulated Gamma Position

Example uses NJ BGS CIEP Load for July.
$400,000
Approximately 80 MWs average load on-peak.

$200,000

$0

($200,000)

($400,000)
Total P&L

($600,000)

($800,000)

($1,000,000)

($1,200,000)

($1,400,000)

($1,600,000)
$0 $50 $100 $150 $200 $250 $300 $350
Average On-Peak LMP

31

Cash Flow Distribution

NJ BGS CIEP Load for July

Swing Risk

32

Cash Flow Distribution with Swing Hedge
NJ BGS CIEP Load for July.
Objective was to reduce CF@R by 50%.

Swing Risk Removed

33

Efficient Frontier Analysis
The efficient frontier tells what the minimum option cost would be to
achieve a particular level of the 5th percentile.
$0

+/- 10% Strangle
($200,000)

($400,000)
5th Percentile

+/- 30% Strangle
($600,000)

($800,000)

($1,000,000)

($1,200,000)
$0 $200,000 $400,000 $600,000 $800,000 $1,000,000 $1,200,000

Option Cost

34

Contact

Eric Meerdink
Director of Structuring & Analytics
Hess Corporation
One Hess Plaza
Woodbridge, NJ 07095

Office: 732-750-6591
Cell: 732-425-4655
Email: emeerdink@hess.com

35

Modeling and Hedging the Risk in Retail Load Contracts

Recommended

Recommended

More Related Content

What's hot

What's hot (16)

Viewers also liked

Viewers also liked (20)

Similar to Modeling and Hedging the Risk in Retail Load Contracts

Similar to Modeling and Hedging the Risk in Retail Load Contracts (20)

Recently uploaded

Recently uploaded (20)

Modeling and Hedging the Risk in Retail Load Contracts

Editor's Notes